Mathématiques, géométrie, Bac Asie 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Dans un repère orthonormé de l’espace, on considère les points A(−3 ; 1 ; 3), B(2 ; 2 ; 3), C(1 ; 7 ; −1), D(−4 ; 6 ; −1) et K(−3 ; 14 ; 14). 1. a. Calculer les coordonnées des vecteurs suivants : . b. Montrer que le quadrilatère ABCD est un rectangle. 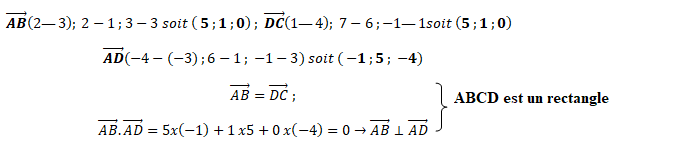c. Calculer l’aire du rectangle ABCD. AB =[52 +12 +02)½ =26½. AD =[(-1)2 +52 +(-4)2)½ =42½. Aire de ce  rectangle : (26 x42)½ =1092½ = (22 x273)½ = 2 *273½.  2. a. Justifier que les points A, B et D définissent un plan. 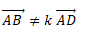Les points A, B et D ne sont pas alignés, donc ils définissent un plan.  b. Montrer que le vecteur n de coordonnées (−2 ; 10 ; 13) est un vecteur normal au plan (ABD). 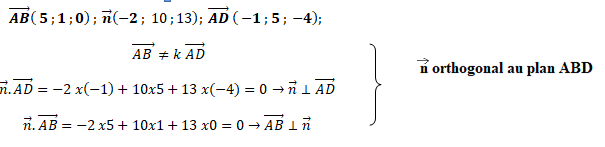 c. En déduire une équation cartésienne du plan (ABD). -2x+10y+13z+d = 0. B appartient à ce plan : -2*2+10*2+13*3+d=0 ; d = -55.  -2x+10y+13z-55 = 0. 3. a. Donner une représentation paramétrique de la droite D orthogonale au plan (ABD) et qui passe par le point K. Le vecteur n de coordonnées (2 ;-10 ; 13) est un vecteur directeur de cette droite. x= -2t+xK = -2t-3. y = 10t+yK=10t +14. z = 13 t+zK = 13 t +14 avec t réel.  b. Déterminer les coordonnées du point I, projeté orthogonal du point K sur le plan (ABD). I appartient au plan (ABD) : -2xI+10yI+13zI-55 = 0. I appartient à la droite D : xI = -2t-3 ; yI = 10t+14 ; zI =13 t+14. -2(-2t-3) +10(10t+14)+13(13t+14)-55 = 0. 273 t +273 =0 ; t = -1. xI =- 1 ; yI = 4 ; zI =1.  c. Montrer que la hauteur de la pyramide KABCD de base ABCD et de sommet K vaut  273½. KI =[(-1+3)2 +(4-14)2+(1-14)2]½ =(4+100+169)½ =273½.  4. Calculer le volume V de la pyramide KABCD. V= aire de la base rectangulaire ABCD x hauteur KI / 3. V = 2 *273½* 273½ / 3 =2 *273 / 3=182 unités de volumes. ... .... Le solide ABCDEFGH est un cube. B(3 ; 0 ; 0), D(0 ; 3 ; 0) et E(0 ; 0 ; 3). On considère les points P(0; 0; 1), Q(0; 2; 3) et R(1; 0; 3).  1. Placer les points P, Q et R sur la figure.  2. Montrer que le triangle PQR est isocèle en R. PR =[(1-0)2 +(0-0)2+(3-1)2]½ =5½. QR =[(1-0)2 +(0-2)2+(3-3)2]½ =5½.  3. Justifier que les points P, Q et R définissent un plan. Les points P, Q et R ne sont pas alignés, donc ils définiqqent un plan.  4. On s’intéresse à présent à la distance entre le point E et le plan (PQR).  a. Montrer que le vecteur u de coordonnées (2 ; 1 ; −1) est normal au plan (PQR).  b. En déduire une équation cartésienne du plan (PQR). 2x+y-z+d=0. P(0 ; 0 ; 1) appartient à ce plan : 0 +0-1+d=0 ; d = 1. 2x+y-z+1=0. c. Déterminer une représentation paramétrique de la droite (d) passant par le point E et orthogonale au plan (PQR). Le vecteur u de coordonnées (2 ; 1 ; -1) est un vecteur directeur de cette droite. x = 2 t +xE = 2t . y = t+yE = t. z = -t+zE = -t +3.  d. Montrer que le point L( 2 /3 ; 1/ 3 ; 8 /3 ) est le projeté orthogonal du point E sur le plan (PQR). Dans cette hypothèse :  L appartient à la droite xL = 2t ; yL = t ; zL =-t+3 L appartient au plan (PQR) : 2xL +yL-zL+1=0. 2 *2t +t-(-t+3)+1=0. 6t =2 ; t = 1 /3 xL = 2 /3 ; yL =1/3 ; zL =-1/3+3= 8 /3. e. Déterminer la distance entre le point E et le plan (PQR). EL = [(2 /3 -0)2 +(1/3-0)2+(8/3-3)2]½ =[4 /9 +1 /9 +1/9]½ =(2 /3)½.  5. En choisissant le triangle EQR comme base, montrer que le volume du tétraèdre EPQR est 2 / 3. Hauteur EP = 2. Base EQR : EQ x ER / 2 = 2 x1 / 2 = 1. V = base x hauteur / 3 = 1x 2 / 3=2 /3.  6. Trouver, à l’aide des deux questions précédentes, l’aire du triangle PQR. V = aire triangle PQR x EL / 3 . Aire de ce triangle = 3 V / EL = 2 x(3/2)½ = 6½.

menu