Une lunette d'amateur pour voir les étoiles doubles, bac Asie 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . .. .. ...... ... La notice d’une lunette astronomique commerciale pour amateur porte les indications suivantes :  Lunette afocale livrée avec deux oculaires de focales 6 mm et 12 mm .  Grossissement jusqu’à 100x  ; Longueur totale 56 cm.  La valeur de la distance focale de l’objectif n’est pas précisée dans la notice.  On se propose de vérifier la cohérence de ces indications entre elles à l’aide d’une modélisation puis d’utiliser cette lunette commerciale pour encadrer la valeur de l’angle sous lequel se présente un système d’étoile double. On modélise la lunette du commerce par deux lentilles minces convergentes (L1) et (L2). L’objectif est modélisé par une lentille (L1) convergente de centre optique O1 et de distance focale f1 ′ .  L’oculaire est modélisé par une lentille convergente (L2) de centre optique O2, et de distance focale f2 ′ . Le schéma n’est pas à l’échelle. Les lentilles (L1) et (L2) sont positionnées pour rendre le système afocal. Estimation de la valeur de la distance focale de l’objectif commercial à l’aide de la lunette modélisée.  Un système optique est dit afocal s’il donne d’un objet à l’infini une image à l’infini. 1. En s’appuyant sur le schéma, justifier que la lunette modélisée est bien afocale. 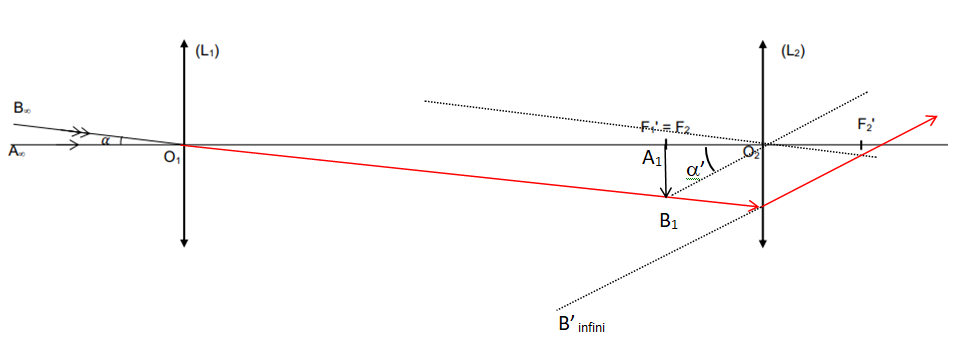L'objet étant à l'infini, son image par L1 se forme au foyer image F1'.  F1' et F2 étant confondus, l'image définitive est rejetée à l'infini. 2. Exprimer la distance O1O2 en fonction des distances focales f1 ′ et f2 ′ pour cette lunette afocale. O1O2  = f1 ′ + f2 ′ .  3. À l’aide des indications commerciales, et en se basant sur le modèle étudié, montrer que la valeur de la distance focale de l’objectif de la lunette commerciale est de l’ordre de 55 cm. O1O2  = 56 cm ; f2 ′  = 0,6 cm ou 1,2 cm. f1 ′ ~56 -1 = 55 cm. Estimation de la valeur du grossissement commercial.  4. Construire l’image A1B1 de l’objet A∞B∞, donnée par l’objectif. On désigne par a le diamètre apparent de l’objet, c’est-à-dire l’angle sous lequel on voit l’objet à l’œil nu.  5. Exprimer tan a en fonction de f1 ′ et A1B1. tan a  ~ a= A1B1 / f1 ′.  L’oculaire (L2) permet d’obtenir une image définitive A′B′ perçue par l’œil sous un angle a′.  6. Sur le schéma, construire la marche d’un rayon lumineux incident issu de B1 émergent de la lentille (L2). 7. Positionner a′ sur le schéma et exprimer tan a′ en fonction de f2 ′ et A1B1. tan a'  ~a'= A1B1 / f2 ′. 8. Rappeler la définition du grossissement G de la lunette et l’exprimer en fonction des distances focales f1 ′ et  f2 ′ . G = a' / a = f1 ′ / f2 ′.  9. Justifier l’intérêt d’utiliser des lentilles telles que f2 ′ ≪ f1 ′ . Le grossissement est très important si f2 ′ ≪ f1 ′ . 10. Compte tenu de la valeur de la distance focale de l’objectif de la lunette commerciale estimée à la question 3, discuter de la cohérence de l’indication « Grossissement jusqu’à 100 × » et préciser si d’autres valeurs du grossissement sont également possibles pour cette lunette commerciale. Oculaire de 6 mm : G = 55 / 0,6 ~ 92. En accord avec le constructeur à 8 % près. Oculaire de 12 mm : G = 55 /1,2 ~46. . ... .... Observation d’étoiles doubles.  Certaines étoiles apparaissent si proches l’une de l’autre qu’il est souvent impossible de les distinguer à l’œil nu pour un observateur sur Terre. L’œil humain ne peut distinguer deux points A et B que si l’angle q sous lequel sont vus les deux points est supérieur à 3,0 × 10–4 rad. On observe un système d’étoiles doubles à travers la lunette commerciale. Avec l’un des deux oculaires fournis, on observe un point lumineux unique tandis qu’avec l’autre on observe deux points lumineux. 11. Préciser les oculaires utilisés pour chaque observation et donner un encadrement de l’angle a sous lequel se présentent les deux étoiles à l’œil nu. a : diamètre apparent de l'étoile double. Si on observe un point unique avec l'oculaire de 12 mm ( G  = 46) :   a < 3,0 10-4 /46 =6,5 10-6 rad. Avec l'oculaire de 6 mm : G = 92. 6,5 10-6 x 92 = 6,0 × 10–4 rad. Cette valeur étant supérieure à à 3,0 × 10–4 rad, on  observe avec la lunette deux points lumineux.

menu