Water bottle flip, bac Asie 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . .. .. ...... ... Le « water bottle flip » est un jeu d’adresse consistant à lancer une bouteille plastique partiellement remplie d’eau afin qu’elle se pose verticalement sur sa base sur une table placée à proximité. Il faut beaucoup s’entraîner pour réussir un « water bottle flip ». Initialement, la bouteille n’est tenue que par son col. Le mouvement ascendant du bras communique la vitesse juste suffisante à la bouteille. Tandis qu’elle monte puis redescend, celle-ci tourne sur elle-même. Dans cet exercice, on se propose d’étudier le mouvement du centre de masse de la bouteille. Le système considéré est l’ensemble {bouteille + eau} de masse 𝑚 = 162 g dont on étudie le mouvement du centre de masse, noté G. Le système évolue dans le champ de pesanteur terrestre  uniforme. On fait l’hypothèse que l’action de l’air est négligeable. Le mouvement est étudié dans le système d’axes (O𝑥𝑦). 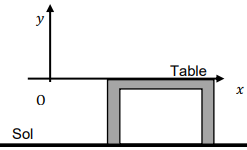À la date 𝑡 = 0 s, le centre de masse G est placé à l’origine du repère O et sa vitesse initiale, notée v0, a une direction faisant un angle a avec l’axe horizontal (O𝑥).  Recherche des conditions initiales sur la vitesse.  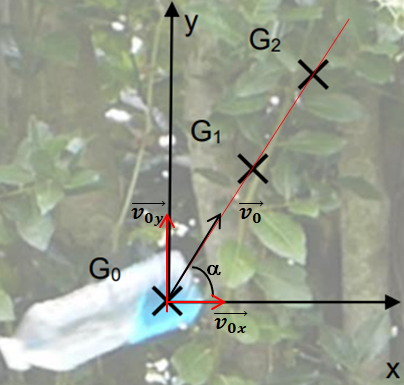Grâce à la vidéo montrant un lancer réussi, on a pu pointer la position du centre de masse G à différents instants.La durée entre deux positions successives est t = 40 ms. L’échelle est donnée par la bouteille dont la hauteur est 18,8 cm.  1. Représenter sur la copie, sans souci d’échelle, le système d’axes (O𝑥𝑦), le vecteur v0, l’angle a ainsi que les coordonnées v0x et v0y et l’allure de la trajectoire du centre de masse de la bouteille. 2. À partir des données expérimentales fournies et de la figure, vérifier que la valeur expérimentale v0 du vecteur vitesse initiale est proche de 3,6 m ⋅ s −1 . G0G1 ~18,8 x 3,8 / 5 ~14,3 cm. v0 ~0,143 / 0,040 ~3,6 m s-1.  3. Proposer une méthode permettant de déterminer expérimentalement la valeur de l’angle a. Projection de G1 sur Ox :2 cm. Projection de G1 sur Oy :3 cm. tan a = 3 / 2 =1,5 ; a ~56°.  Modélisation du déplacement du centre de masse.  4. En précisant la loi utilisée, donner les expressions des coordonnées du vecteur accélération a du centre de masse. La bouteille n'est soumise qu'à son poids verticale vers le bas, valeur mg. La seconde loi de Newton conduit à : ax = 0 et ay = -g.  5. En déduire les expressions des coordonnées vx(𝑡) et vy(t) du vecteur vitesse du centre de masse et montrer que les équations horaires du mouvement sont :   x(t)= v0 cos a t ;  y(t)=-½gt2 + v0 sin a t . Le vecteur vitesse est une primitive du vecteur accélération et v0x = v0 cos a , v0y = v0 sin a . vx = v0 cos a , v0y =-gt + v0 sin a . Le vecteur position est une primitive du vecteur vitesse et la position initiale est l'origine du repère. x(t)= v0 cos a t ;  y(t)=-½gt2 + v0 sin a t . Pour déterminer la distance à laquelle tombe la bouteille par rapport au point O, on crée un programme en langage python dont un extrait est présenté ci-dessous. Ce programme utilise les équations horaires modélisant le déplacement du centre de masse et les valeurs expérimentales : v0 = 3,6 m ⋅ s −1 𝛼 = 59 ° 𝑔 = 9,81 m ⋅ s −2 . . ... .... L’exécution de ce programme permet d’obtenir le graphique ci-dessous qui modélise l’évolution des coordonnées (𝑥, 𝑦), exprimées en mètre, du point G au cours du temps. 6. Associer chacun de ces tracés à 𝑥(𝑡) et 𝑦(𝑡).  7. Préciser ce qui est caché par le rectangle gris dans la ligne 15 du programme (expression ou valeur).  On estime que le centre de masse G se trouve à une hauteur voisine de 2 cm du fond de la bouteille lorsque celle-ci se pose sur la table.  8. Estimer la durée du mouvement de la bouteille obtenue par la modélisation. t ~0,58 s. La durée du mouvement de la bouteille lors de la réalisation de ce « water bottle flip » a été mesurée. On a obtenu Dt = (0,50 ± 0,05) s.  9. Proposer au moins une explication permettant de rendre compte de l’écart entre cette durée réelle et la durée obtenue par la modélisation. Dans la modèlisation  : - on ne tient pas compte des frottements. - on ne prend pas en compte le mouvement de l'eau lors de la rotation de la bouteille. 10. À l’aide du modèle, déterminer la distance à laquelle la bouteille tombe sur la table par rapport à l’origine du repère. Indiquer ce qu’il est possible de prévoir pour la distance réelle. x(t= 0,58) ~1,1 m d'après le graphique. x(t= 0,50) ~0,95 m, distance réelle.

menu