Cave à vin, bac Asie 2021.

Partie 1 – Evolution de la température.
On s’intéresse à l’évolution de la température 𝑇 du système {vin + bouteille} placé dans le thermostat. Le système {vin + bouteille} est immobile. L’air de la cave à vin est ventilé. On désigne par Q le transfert thermique entre l’air et le système, et par F le flux thermique correspondant, c’est-à-dire le transfert thermique par unité de temps. Le transfert thermique et le flux thermique sont comptés positivement si le transfert thermique a lieu de l’air vers le système. On fait l’hypothèse que le flux thermique F vérifie la loi phénoménologique de Newton.
Lorsqu’un système incompressible de température 𝑇 est placé dans un fluide en écoulement à la température T_a , il s’établit un flux thermique entre le thermostat et le système proportionnel à l’écart de température (T-T_a). On peut alors écrire :
F = −h S (T − T_a)
S (en m² ) est la surface d’échange entre le système et le thermostat ;
h (en W ⋅ m⁻² ⋅ K⁻¹ ) est le coefficient d’échange convectif .
Surface d’échange entre la bouteille et l’air :S = 4,66 × 10⁻² m² ; Coefficient d’échange convectif : h= 10 W ⋅ m⁻² ⋅ K⁻¹ .
Capacité thermique du système {vin + bouteille} : 𝐶 = 3,25 kJ ⋅ K ⁻¹.

1. À l’aide du premier principe de la thermodynamique, relier la variation d’énergie interne DU du système {vin + bouteille} au transfert thermique Q entre l’air et le système.
DU = Q.
2. Exprimer le transfert thermique Q pendant une durée très petite Dt en fonction du flux thermique F supposé constant pendant cette durée et de Dt. Rappeler les unités, dans le système international, des grandeurs intervenant dans cette expression.
Q = F Dt.
Q (joule) ; F(watt) ; Dt ( seconde).
La variation d’énergie interne d’un système incompressible au repos dont la température varie de DT est donnée par la relation
DU = C DT. (𝐶 est la capacité thermique du système).
3. Exprimer le flux thermique en fonction de la capacité thermique C du système supposé incompressible, de sa variation de température DT et de la durée Dt.
F = C DT / Dt.
4. En utilisant la loi phénoménologique de Newton, et en faisant tendre Dt vers 0, vérifier que l’équation différentielle qui régit l’évolution de la température T s’écrit :
dT / dt= − 1 / t (T − T_air). En déduire l’expression et l’unité de t.
F = −h S (T − T_air) = C DT / Dt.
dT / dt = -h S / C (T − T_air).
On pose t = C / (hS).
C s'exprime en J K^-1 et hS s'exprime en WK^-1 ; t s'exprime en J W^-1 soit en seconde.

Le modèle d’évolution temporelle de la température du système {vin + bouteille}, solution de l’équation différentielle, est le suivant : 𝑇(𝑡) = (𝑇₀ − 𝑇_𝑎𝑖𝑟) 𝑒xp( − t / t) + 𝑇_𝑎𝑖𝑟. Cette évolution temporelle de la température 𝑇(𝑡) est représentée ci-dessous.

5. Retrouver à l’aide des résultats de la modélisation les valeurs de 𝑇₀ et de 𝑇_𝑎𝑖𝑟.

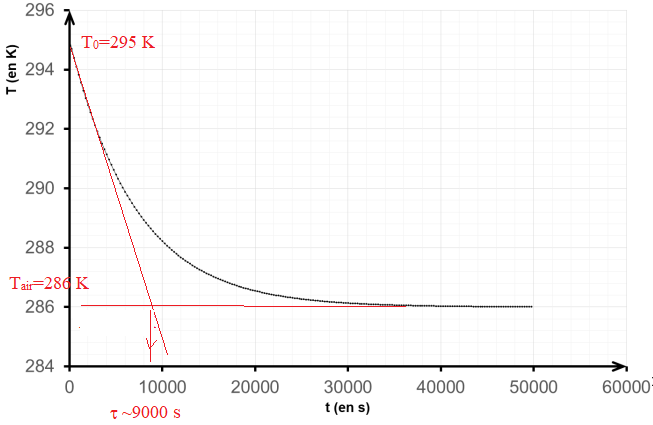6. Estimer graphiquement au bout de combien de temps le vin pourra être servi à la température souhaitée (à 0,5 degré près).
On s’intéresse à une bouteille de vin rouge léger dont la température idéale de service est de 13° C. Initialement, cette bouteille et son contenu sont à une température voisine de 22° C. On place cette bouteille dans la cave à vin afin d’optimiser sa dégustation. L’air à l’intérieur de la cave à vin joue le rôle d’un thermostat. Sa température T_air demeure constante et égale à 13 °C.
Au bout de 20 000 s, la température du vin est de 13 ± 0,5 °C.
.