Parker solar probe, bac Asie 2021.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts.


.
.
.. ..
......


...
La NASA, l’agence spatiale am�ricaine, a lanc� en direction du Soleil une sonde spatiale, PSP (Parker Solar Probe), dont la mission est d’�tudier la couronne solaire. La sonde PSP doit relever de nombreux d�fis, notamment :
- atteindre une orbite permettant d’approcher le Soleil de tr�s pr�s ;
 - prot�ger les instruments de mesure des rayonnements intenses.
Partie 1.
Les caract�ristiques orbitales de la sonde Depuis son lancement le 12 ao�t 2018, la sonde PSP subit des modifications successives de son orbite autour du Soleil du fait de l’assistance gravitationnelle de la plan�te V�nus. Elle rejoint ainsi progressivement son orbite optimale qui lui permettra de passer au plus pr�s du Soleil d�but 2025. La sonde effectuera alors quatre passages au p�rih�lie P et pourra enregistrer un maximum de donn�es exp�rimentales.
Masse du Soleil MS = 2,0 � 1030 kg.  Constante gravitationnelle G = 6,67 � 10−11 m3 ⋅ kg −1 ⋅ s
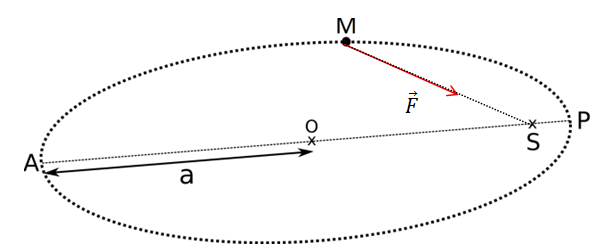
2 1. Sur la figure suivante, on a repr�sent� l’orbite elliptique que la sonde PSP d�crira autour du Soleil en 2025. Les points A et P sont respectivement l’aph�lie et le p�rih�lie. Le point S repr�sente le centre du Soleil.
1.1. Repr�senter sur la figure et sans souci d’�chelle, la force d’attraction gravitationnelle, not�e F, mod�lisant l’action exerc�e par le Soleil sur la sonde PSP lorsqu’elle est au point M.
 
1.2. En utilisant la 2�me loi de Kepler, comparer la valeur vP de la vitesse de la sonde au point P � la valeur vA de la vitesse de la sonde au point A.

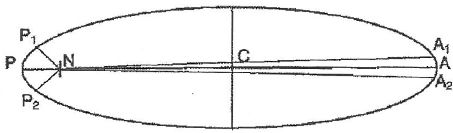Le mouvement de la sonde est tel que le segment de droite reliant le centre du soleil et la sonde balaie des aires �gales pendant des dur�es �gales.
La distance A1 A2 est inf�rieure � la distance P1 P2.
Les dur�es de parcours entre les points A1 et A2 puis P1 et P2 sont �gales.
Donc la vitesse moyenne entre les points A1 et A2 est sup�rieure � celle entre les points P1 et P2.
2. La NASA pr�voit que la valeur vP de la vitesse de la sonde au point P sera de 192 km ⋅ s −1 avec une incertitude-type de l’ordre de 5 km ⋅ s −1 . On souhaite savoir si cette valeur de la vitesse a �t� d�termin�e � l’aide du mod�le du mouvement circulaire pour la sonde PSP sur son orbite autour du soleil ou si un autre mod�le a �t� utilis�. On se propose donc de d�terminer la valeur v de la vitesse de la sonde PSP en supposant que son mouvement est circulaire, de rayonr SP= 6,9 � 106 km, afin de la comparer � celle pr�vue par la NASA. Le r�f�rentiel h�liocentrique est consid�r� comme galil�en.

2.1. � l’aide de la 2e loi de Newton, montrer que, dans le cas d’une trajectoire circulaire, la vitesse v de la sonde PSP est constante et a pour expression : v= (GMS / r)�  avec MS la masse du Soleil et r le rayon de la trajectoire circulaire.

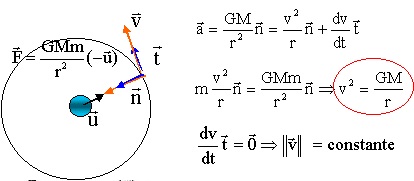 2.2. Calculer la valeur v de la vitesse de la sonde PSP dans le cadre de ce mod�le.
v= (6,67 10-11 x2 1030 / (6,9 109)� =1,4 105 m /s = 1,4 102 km /s.
 2.3. Apporter une conclusion � la probl�matique pos�e dans cette question 2.
192 et 140  diff�rent de plus de 5 km /s.
Le mod�le d'une trajectoire circulaire est � rejeter.

La 3�me loi de Kepler lie le demi-grand axe orbital et la p�riode de r�volution des syst�mes (plan�te, sonde) en orbite autour du Soleil. On peut ainsi d�terminer la p�riode de r�volution de la sonde PSP autour du Soleil � partir de la mesure du demi-grand axe de sa trajectoire elliptique.
3. En utilisant la 3�me loi de Kepler et apr�s analyse du programme Python figurant ci-apr�s et de ses r�sultats, d�terminer la p�riode de r�volution T de la sonde PSP autour du Soleil.
Troisi�me loi de kepler : T2 = Cste a3.
a = 5,821 107 km.
Cste = 3,9835 10-20 J2 km-3.
T2 =3,9835 10-20 x(5,821 107)3 =7,86 103 j2.
T =88,6 j.
 .

...
....

 Partie 2 - Les panneaux photovolta�ques.
Durant la mission, les panneaux photovolta�ques de la sonde PSP servent � fournir l’�nergie �lectrique n�cessaire au fonctionnement des instruments de mesure embarqu�s. Ils permettent d’obtenir une puissance �lectrique utile Pel = 340 W. En 2025, au plus pr�s du Soleil, ils devront �tre refroidis. Une puissance thermique Pth devra alors �tre �vacu�e gr�ce � de l’eau sous pression circulant entre les panneaux photovolta�ques et des radiateurs. Lorsque le bouclier sera parfaitement orient� vers le Soleil, la puissance thermique � �vacuer Pth sera 13 fois sup�rieure � la puissance �lectrique utile ; une erreur d’inclinaison du bouclier thermique de 1� entrainera une puissance thermique suppl�mentaire � dissiper de 35%.
 Dans les questions suivantes, on se place dans le cas critique d’une erreur de 1� d’inclinaison du bouclier thermique.
Masse volumique de l’eau liquide dans les conditions de pression et de temp�rature de la sonde PSP : reau = 0,958 kg ⋅ L −1 .
Dur�e du passage � proximit� du Soleil : Dt = 110 h.
 Pression de l’eau dans le circuit : 5 bar.
Temp�rature d’�bullition de l’eau sous 5,0 bar : Teb= 150�C.
 Capacit� thermique massique de l’eau : Ceau = 4185 J ⋅ K −1 ⋅ kg −1.

4. Sachant que les radiateurs peuvent dissiper une puissance maximale Pd max = 6000 W, montrer que ces radiateurs peuvent effectivement dissiper la puissance thermique c�d�e par les panneaux photovolta�ques � l’eau sous pression. Pendant la dur�e Δ𝑡 du passage � proximit� du Soleil, l’�quivalent d’un volume d’eau Veau = 7 570 L va circuler pour refroidir les panneaux solaires. La temp�rature de ce volume d’eau va passer de la valeur Tmin = 50�C � une valeur maximale Tmax que l’on cherche � d�terminer.
 On consid�re ici que la puissance thermique re�ue par ce volume d’eau est Pth max = 6 000 W.
Puissance thermique � �vaquer :
13 Pel x1,35 =13 x340 x1,35 =5,97 103 W.
Cette valeur �tant inf�rieure � 6000 W, , les radiateurs peuvent dissiper cette puissance thermique.

5. Donner l’expression de l’�nergie thermique QR re�ue par l’eau en fonction de Pth max et Dt.
QR = Pth max x Dt.
 6. En supposant que l’�l�vation de temp�rature du volume total d’eau est uniquement due aux panneaux solaires, d�terminer la temp�rature Tmax atteinte et d�terminer si le syst�me de refroidissement risque ou non l’explosion.
QR = 6000 x  110 x 3600 =2,376 109 J.
Masse d'eau m = Veau  reau= 7 570 x 0,958 =7,250 103 kg.
QR =m Ceau DT ; DT = QR /(mCeau) =2,376 109 / ( 7,250 103 x 4185) ~ 78�C.
Tmax = 50 +78 = 128 �C.
Cette valeur �tant inf�rieure = 150 �C, il n'y a pas de risque d'explosion.

Partie 3 - Le bouclier thermique.
 La sonde PSP est prot�g�e des rayonnements solaires par un bouclier thermique de surface Sb et d’�paisseur e.. Constamment tourn� vers le Soleil, ce bouclier thermique permet de garder l’ensemble du corps de la sonde � une temp�rature convenable pour ne pas endommager les instruments embarqu�s. Le bouclier thermique est compos� d’un rev�tement externe � base d’alumine, capable d’endurer de hautes temp�ratures jusqu’� 1900 K. Derri�re ce rev�tement, se trouve de la mousse de carbone, prise entre deux couches rigides en fibre de carbone, tr�s r�sistantes � la temp�rature et � la d�formation.
Soumis � l’intense rayonnement du Soleil, la temp�rature � l’avant du bouclier atteint une valeur Tav = 1700 K et rayonne un flux thermique surfacique important jav. Par ailleurs, un flux thermique surfacique jar = 1,55 kW ⋅ m−2 traverse la surface Sb = 16,6 m2 du bouclier vers l’arri�re. Pour permettre le bon fonctionnement de la sonde, il est imp�ratif de limiter l’�l�vation de temp�rature � l’arri�re du bouclier thermique en d�pit de ce flux thermique surfacique �lev�.
7. Caract�riser le mode de transfert thermique entre le Soleil et la sonde PSP.
Transfert par rayonnement.
 8. Justifier l’utilisation de la mousse de carbone � l’int�rieur du bouclier thermique.
La conductivit� thermique de la mousse de carbone est tr�s faible  l = 0,0262 W m-1 K-1.
9. D�terminer la valeur du flux thermique total vers l’arri�re F.
F = jar Sb =1,55 x16,6 =25,73 ~25,7 kW.
10. � l’aide des caract�ristiques du bouclier thermique et des donn�es, d�terminer l’�cart de temp�rature |DT| entre les deux faces du bouclier thermique ainsi que la temp�rature Tar � l’arri�re du bouclier. Commenter
e =11,4 cm , conductivit� thermique du bouclier 0,140 W m-1 K-1.
R�sistance thermique du bouclier : Rth = e / (l Sb) =0,114 / (0,140 x16,6) =0,049 K W-1.
|DT| =Rth F =0,049 x25,7 103 =1,26 103 K.
Tar =1700-1,26 103  ~440 K soit environ 167 �C.
Cette temp�rature n'est pas convenable et peut endommager les instruments embarqu�s.


  
menu