Freinage en ligne droite, bac Asie Pacifique 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . .. .. ...... ... Etude de la prise de risque d'un pilote de formule 1 pendant un freinage sur un circuit. Modèle simple. Le système se déplace à l'horizontale, en ligne droite, à grande vitesse. Il freine du point A au point B avant d'entrer dans un virage. Le système subit : son poids. La résultante des forces exercée par la route que l'on peut décomposer en deux forces : RN verticale vers le haut compensant le poids., f force horizontale,constante,  de sens opposé au déplacement modélisant l'ensemble des frottements subis par la voiture. Le freinage commence à la date t=0 lorsque le centre de masse se trouve en A La vitesse vaut vA = 321 km / h. 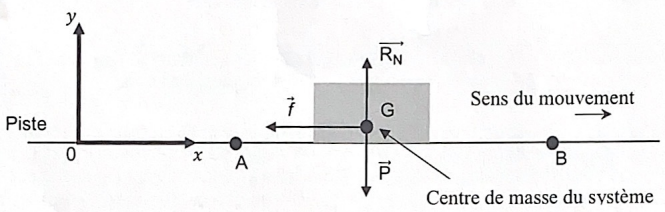1. Montrer que les coordonnées du vecteur accélération sont ax(t) = -f / m et ay(t) = 0. Ecrire la seconde loi de Newton :  sur l'axe Ox : -f = max(t) ; ax(t) = -f / m. sur l'axe vertical, les forces se compensent, donc ay(t) = 0. On désigne par Dv = vB-vA la variation de la vitesse entre A et B et par Dt la durée du mouvement entre A et B. 2. Justifier que ax(t) = Dv  / Dt . La durée Dt étant très courte on peut assimiler Dt à dt et Dv à dv(t). La vitesse passe de 321 km /h à 84 km /h pendant 1,50 s. 3. Calculer ax(t) et la comparer à la valeur 6 G mentionnée dans le texte introductif ( 1 G = 9,81 m s-2). 4. Déterminer le volume de solution mère ( titre massique 100 mg / L) à prélever pour préparer V = 50,0 mL de la solution n°2. variation de la vitesse : (84 =321 ) /3,6 ~ -66 m /s. ax(t) = -66 / 1,5 = -44 m s-2 soit environ 4,5 G. La figure suivante indique les limites de tolérance d'un individu tenant compte de la valeur de l'accélération ( en G) et la durée pendant laquelle il la subit. 4. Indiquer si le pilote prend des risques au cours du freinage. 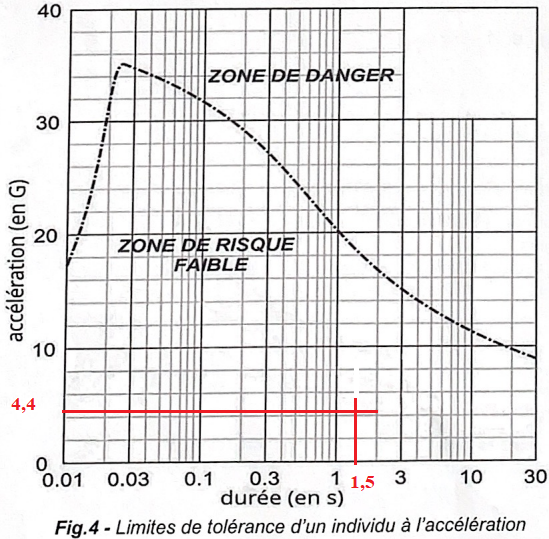Le pilote ne prend pas de risque. Validité du modèle simplifié. On compare l'évolution de la vitesse prévue par le modèle à celle conduite des mesures réalisées par des capteurs embarqués. 5. Dans le cadre du modèle simplifié, montrer que la coordonnée vx(t) du vecteur vitesse a pour expression : vx(t) = -f /m t + vA avec vA = 89 m /s. La vitesse est une primitive de l'accélération : vx(t) = -f / m t + Cste. A t = 0, vx =Cste = vA = 321 / 3,6 =89 m /s. 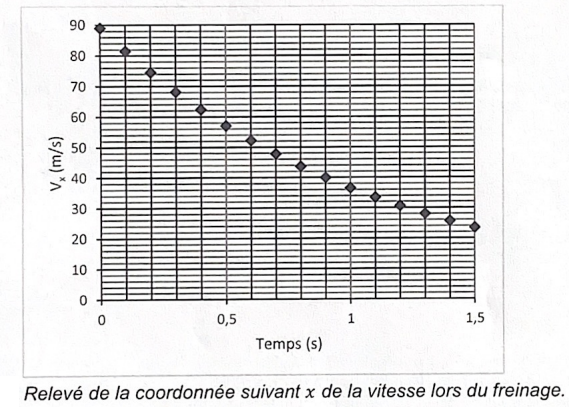6. Comparer l'allure de ce graphe avec l'allure prédite par le modèle. Le modèle indique une fonction affine du temps.. L'expérience ne conduit pas à une fonction affine du temps. 7. Quelle hypothèse du modèle doit êtr remis en cause ? Les forces de freinage ne sont pas constantes au cours du temps.

menu