E3C première, masse, tension, fréquence.

Partie 1 : masse et fréquence.
On dispose de trois marteaux M₁, M₂ et M₃ de masses respectives m₁=0,24 kg, m₂=0,48 kg et m₃=1,44 kg.
L’expérience consiste à les laisser tomber sur une enclume. Un logiciel d’acquisition enregistre le signal sonore émis.
On désigne respectivement par f₁, f₂ et f₃ les fréquences fondamentales des sons émis par les marteaux M₁, M₂ et M₃ lors de l’expérience.
1- Lire les fréquences fondamentales f₁, f₂, et f₃ des sons émis lors de l’expérience et noter leurs valeurs.
2- Comparer ces fréquences. La masse du marteau influe-t-elle sur la fréquence fondamentale du son émis ?

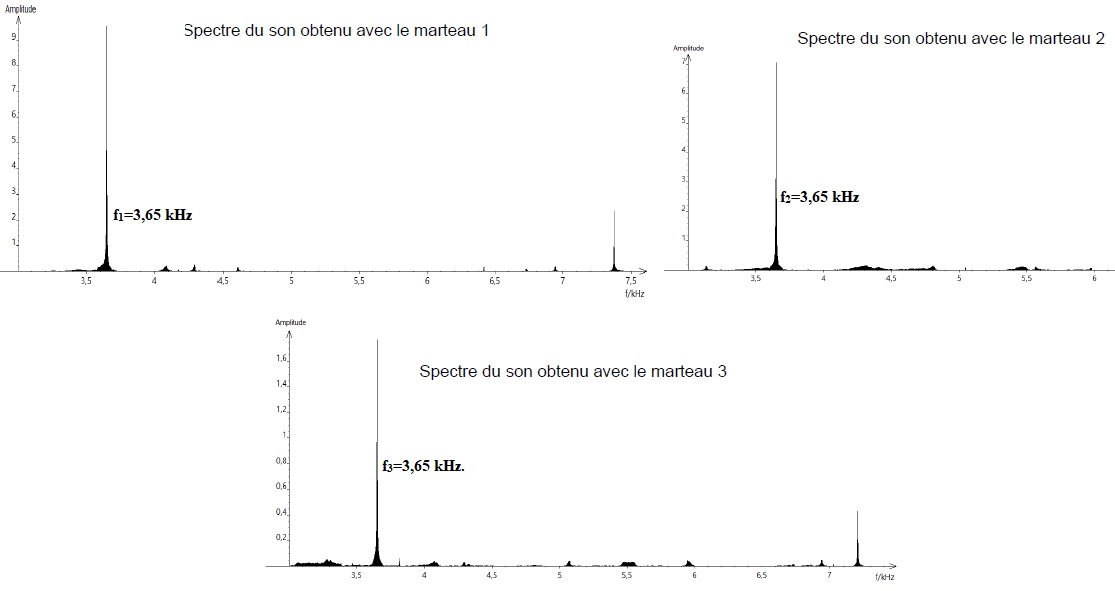
Les fréquences du fondamentale des sons sont identiques. La masse n'a pas d'influence sur ces fréquences.
Partie 2 : tension et fréquence.
Dans cette partie, on tend une corde de longueur quelconque à l'aide d'une masse variable m

On a relevé dans le tableau ci-dessous les fréquences fondamentales obtenues en pinçant la corde :

masse ( kg)	0	8,070	9,990	11,110
fréquence ( Hz)	0	202	224	237
fréquence / masse	xxx	25,03	22,42	21,33

3- Peut-on affirmer que la fréquence fondamentale du son est proportionnelle à la masse utilisée pour tendre la corde ? Justifier par la méthode de votre choix.
Le rapport fréquence / masse n'est pas constant : la fréquence fondamentale du son n' est pas proportionnelle à la masse.
4- On propose de modéliser la manière dont la fréquence fondamentale varie en fonction de la masse à l'aide d'une fonction définie sur l'ensemble des réels positifs. On considère les trois fonctions suivantes : g(m)= 9 /4 m² ; h(m)=71x m^½ et j(m)= 25m.
Les trois fonctions g,h et j sont représentées graphiquement.
. 4-1- Pour chaque fonction g,h et j, retrouver la courbe qui la représente.

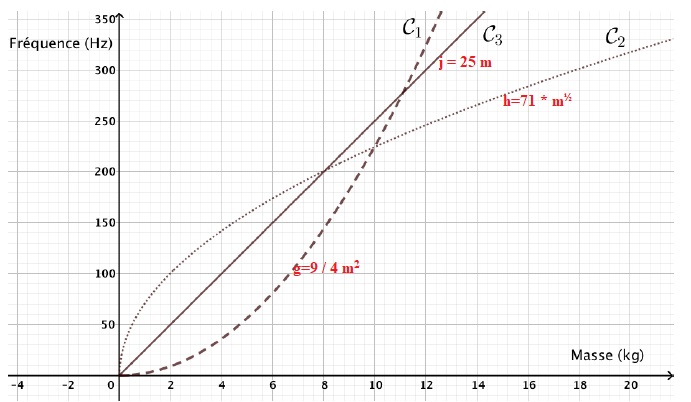
4-2- Quelle fonction modélise le mieux le problème ? Justifier.
:

masse ( kg)	0	8,070	9,990	11,110
fréquence ( Hz)	0	202	224	237
fréquence / racine carrée(masse)	xxx	71,1	70,87	71,1

La fonction h= 71 * m^½ modélise le mieux le problème.
Partie 3 : analyse de document.
Voici un extrait du Commentaire au songe de Scipion écrit par Macrobe aux alentours de 400 après JC.
« [...] la diversité des sons, indépendante des hommes, correspondait aux marteaux. Alors il mit tout son soin à en évaluer le poids, et après avoir noté la différence de poids qui caractérisait chacun il fit fabriquer des marteaux de poids différents, en plus ou en moins ; les sons produits par leurs coups ne ressemblaient en rien à ceux d’avant et ne s’accordaient plus aussi bien. Il constata alors que l’harmonie sonore était réglée par les poids, et après avoir relevé les nombres qui définissaient la diversité bien accordée de ces poids, il passa des marteaux à l’examen des instruments à cordes : il tendit des boyaux de mouton ou des nerfs de boeuf en y attachant des poids aussi variés que ceux qu’il avait découverts à propos des marteaux, et il en résulta bien le genre d’accord que lui avait fait espérer son observation antérieure, à laquelle il ne s’était pas livré pour rien. » Commentaire au songe de Scipion, II, 1, 9-13
5- En quelques lignes, émettre une critique scientifique des affirmations contenues dans le Commentaire au songe de Scipion.
Les spectres des sons émis lors de la chute des marteaux de masses différentes sur une enclume possède la même fréquence du fondamentale mais des harmoniques un peu différentes. L'harmonie sonore n'est pas réglée par la masse.
Par contre, la fréquence du fondamental des sons émis en pinçant une corde tendue, dépend bien de la tension de la corde. Dans ce cas, l’harmonie sonore est réglée par les masses.