E3C première, la guitare électrique.

La guitare électrique est composée de six cordes métalliques. Une corde est dite « à vide » lorsqu'elle vibre sur toute sa longueur.
Les fréquences des notes produites par les cordes à vide d’une guitare bien accordée sont données dans le tableau suivant :

n° de la corde	1	2	3	4	5	6
note ( le chiffre indique le numéro de l'octave)	mi₁	la₁	ré₂	sol₂	si₂	mi₃
fréquence ( Hz)	82,4	110,0		196,0	246,9

2- La gamme tempérée, représentée ci-dessous, est construite en divisant l’octave en douze intervalles égaux (au sens où les rapports entre deux fréquences successives sont égaux), appelés demi-tons.

Parmi les algorithmes ci-dessous, indiquer celui qui permet de calculer la fréquence du Ré₂ à partir du Sol₂. Calculer cette fréquence.

algorithme 1	algorithme 2	algorithme 3	algorithme 4
f =196 Pour i allant de 1 à 5 : f =f / 2^1/12 Fin pour	f =196 Pour i allant de 1 à 5 : f =f x 2^1/12 Fin pour	f =196 Pour i allant de 1 à 6 : f =f / 2^1/12 Fin pour	f =196 Pour i allant de 1 à 6 : f =f x 2^1/12 Fin pour

5 intervalles entre le sol₂ et le ré₂.
196 / 2^5/12 = 146,8 Hz. ( algorithme 1 ).
3 - Comme tous les instruments de musique, une guitare électrique doit être accordée. Il faut pour cela vérifier que les fréquences des sons émis par les cordes à vide sont égales à cellesindiquées ci-dessus.
Un système d'acquisition a permis d’enregistrer et de visualiser le signal correspondant au son émis par la corde n°2 d’une guitare électrique jouée à vide.
Indiquer si la corde n°2 de la guitare électrique est accordée. Justifier la réponse.

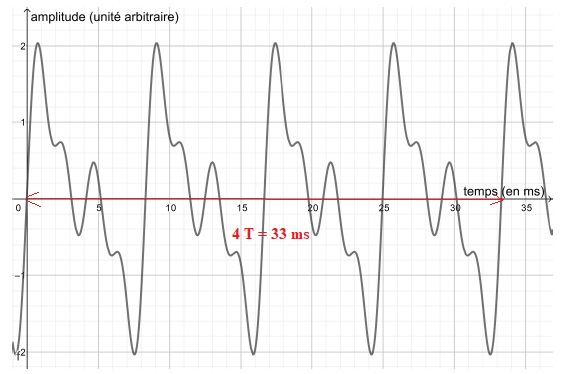
T= 33 10^-3 / 4 ; f = 1 / T = 4 10³ / 33 ~121 Hz., valeur différente de 110 Hz. Cette corde n'est pas accordée.
4- La fréquence du son émis par une corde mise en vibration dépend de plusieurs paramètres dont la longueur L et la force de tension T de la corde.
Expérience 1 : on fait varier la longueur L de la corde et on mesure la fréquence f du son émis (la force de tension T de la corde est
maintenue constante).
Expérience 2 : on fait varier la force de tension T de la corde et on mesure la fréquence f du son émis (la
longueur L de la corde est maintenue constante).

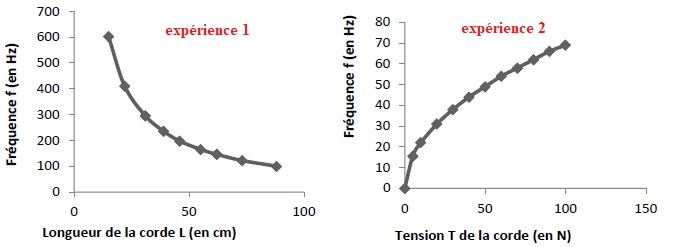
4-a- Indiquer comment varie la fréquence de la corde en fonction de la longueur.
La fréquence diminue quand la longueur de la corde croît. A tension constante, f est divisée par 2 quand la longueur double.
4-b- Indiquer comment varie la fréquence de la corde en fonction de la tension.
A longueur fixée, la fréquence et la tension varient dans le même sens. Fréquence et tension ne sont pas proportionnelles, la courbe n'étant pas une droite passant par l'origine..
4-c- On propose ci-dessous quatre relations entre la fréquence f du son produit par une corde et les paramètres qui l’influencent. k est une constante qui dépend de la corde.
A) f = k T^½ / L. B) f = kT / L. C) f = kL T^½. D). f = k(T L)^½.
Choisir et recopier sur la copie la relation qui convient.
T doit figurer au numérateur avec un exposant différent de 1 et L au dénominateur. f = k T^½ / L.
4-d- Un guitariste souhaite accorder sa guitare. Pour cela, il peut agir sur les différentes clés pour augmenter ou diminuer la tension des cordes. Avant accord, le son émis par la corde n°4 à vide est de 192,0 Hz.
Indiquer comment il doit agir pour accorder la corde n°4 de sa guitare.
La fréquence doit être égale à 196 Hz. Il faut augmenter la tension de la corde n° 4.