L’Union européenne a interdit le commerce de l’ivoire depuis 1989, à l’exception de celui des antiquités acquises avant 1947.
Selon un rapport remis à la Commission européenne en juillet 2018,
l’ivoire vendu en Europe proviendrait pourtant essentiellement de
défenses d’éléphants abattus récemment. Ce rapport s’appuie sur des
résultats obtenus par datation au carbone 14C de l’ivoire
saisie par les autorités. Les trafiquants contournent la loi en faisant
passer l’ivoire récent pour de l’ivoire ancien.
Partie A.
1- Parmi les propositions suivantes, quelle est celle qui correspond à la désintégration du carbone 14 ?
a) 188O→146C + 42He.
b) 146C→147N + 0-1e. Vrai.
c) 62He + 84Be →146C.
2- La demi-vie du carbone 14 est de 5730 ans. Expliquer le terme « demi-vie ».
La demi-vie ou période radioactive est la durée au bout de laquelle la
moitié des atomes de carbone initiaux se sont désintégrés.
3- On considère un
échantillon d’ivoire d’éléphant contenant à un instant donné 16
milliards de noyaux de carbone 14. Calculer le nombre de noyaux de
carbone 14 restants au bout de :
3-a- 5 730 ans.
La motié soit 8 milliards.
3-b- 11 460 ans = 2 x5730 ans.
Le quart soit 4 milliards.
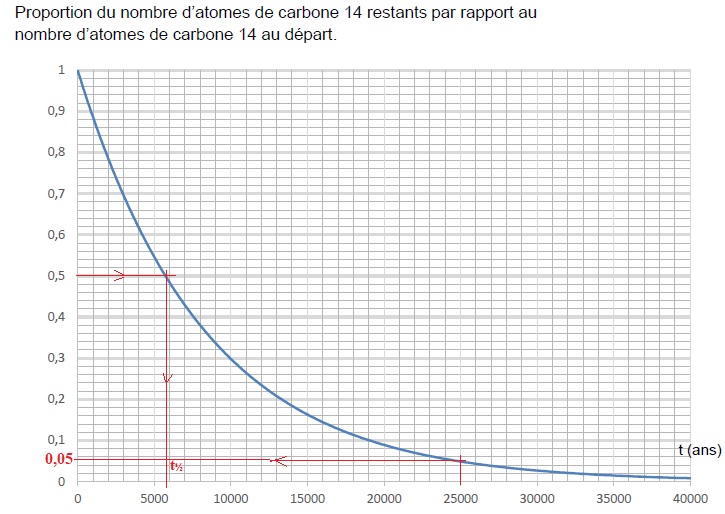
4- Repérer sur le graphique la valeur de la demi-vie du carbone 14. On fera figurer les traits de construction sur la courbe.
5- Estimer la proportion du nombre de noyaux de carbone 14 restants après 25 000 ans.
Partie B.
On s’intéresse désormais à la datation au carbone 14 d’échantillons
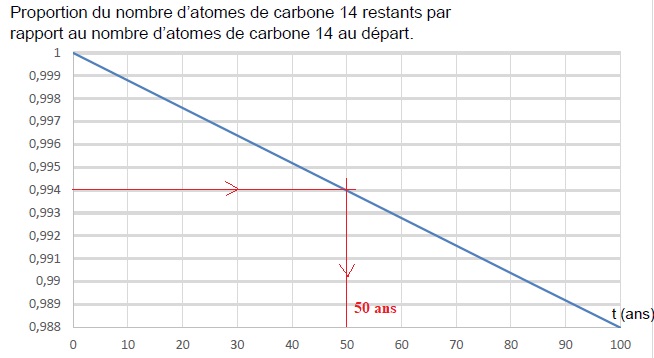
d’ivoire plus récents. Sur une période de 100 ans, on peut approcher la
portion de courbe précédente par un segment de droite représenté ci-dessous.
6- En 2019, l’analyse d’un échantillon d’ivoire d’éléphant a permis
d’estimer à 0,994 la proportion d’atomes de carbone 14 restants par
rapport au nombre initial d’atomes de carbone 14.
6-a- Dater la mort de l’éléphant.
6-b- Cet ivoire provient-il d’un éléphant abattu illégalement ? Justifier la réponse.
Cet ivoire est récent, l'éléphant a été abattu illégalement.
7-
L’objectif des trois sous-questions suivantes est d’étudier la validité
du modèle affine précédent pour un nombre d’années supérieur à 100.
7-a- On note f la
fonction affine ayant pour représentation graphique la droite
ci-dessus. Parmi les expressions suivantes, dans lesquelles t est
exprimé en années choisir celle de f :
a) f(t) = −1,2×10−4 t + 1
b) f(t) = 1,2×10−4 t + 1
c) f(t) = −8,3×102 t+ 1.
Coefficient directeur de la droite : (0,988-1) / (100-0) = -1,2 10-4. Réponse a.
7-b- Calculer f(5730).
f(5730) = -1,2 10-4 x 5730 +1 =0,3124.
7-c- Expliquer pourquoi on peut en déduire que ce modèle n’est pas pertinent pour des durées comparables à une demi-vie.
f(t½) calculé par ce modèle linéaire donne 0,3124, valeur très différente de 0,5.

