E3C première, détermination de l'âge de la terre.

1- Buffon présente sa démarche pour trouver l’âge de la Terre. Il modélise la Terre par une boule de matière en fusion qui se refroidit.
1-a- Indiquer les trois étapes du refroidissement de la Terre décrites par Buffon.
Passage de l'état liquide à l'état solide jusqu'au centre de la terre.
Refroidissement du solide jusqu'à à une température voisine de 50 °C.
Refroidissement du solide jusu'à la température actuelle de la terre.
1-b- Donner l’argument sur lequel s’appuie Buffon pour réévaluer sa première estimation de l’âge de la Terre.
La terre n'est pas entièrement constituée en grande partie de fer mais de matières vitrecibles et calcaire qui se refroidissent plus vite que le fer
2- À partir d’expériences, Buffon établit les données contenues dans le tableau ci-dessous, donnant le temps de refroidissement « au point de pouvoir la toucher sans se brûler » (en minute) d’une boule de fer en fonction de son diamètre (en demi-pouces) :

diamètre d ( en demi-pouce)	1	3	5	7	9
temps de refroidissement observé ( minutes)	12	58	102	156	205

Dans le repère, placer les points représentant les données du tableau, puis tracer la droite passant par les points d’abscisses 3 et 9.

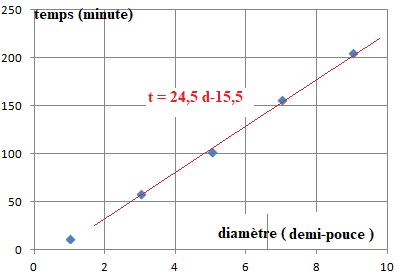
3- On suppose que la Terre a un diamètre égal à 12 740 km, c’est-à-dire à environ 1 milliard de demi-pouces.
La droite précédemment tracée a pour équation t=24,5×d−15,5, où t est la durée de refroidissement (en minute) et d
le diamètre de la boule (en demi-pouce). En supposant que cette droite modélise l’évolution du temps de refroidissement en fonction du diamètre, retrouve-t-on les 46 991 années obtenues par Buffon comme temps de refroidissement d’une boule de fer de la taille de la Terre ? Présenter les calculs permettant de répondre à la question.
t = 24,5 x10⁹ -15,5 =2,45 10¹⁰ minutes soit 4,08 10⁸ heures soit 1,70 10⁷ jours soit 4,66 10⁴ ans, valeur proche de celle obtenue par Buffon.

Deuxième Partie
Des méthodes de datation de l’âge de la Terre plus récentes font intervenir la décroissance radioactive. Lors de la formation de la Terre, de l’uranium naturel s’est créé, en particulier l’isotope radioactif ²³⁵U. L’examen de roches montre qu’aujourd’hui, il reste environ 1 % de l’uranium 235 présent lors de la formation de la Terre.
4- Le graphique suivant représente le nombre de noyaux d’uranium 235 restants en fonction du temps. On note N₀ le nombre de noyaux à l’instant initial t=0.
4-a- Sur ce graphique, repérer la demi-vie t_½ de l’uranium 235. Faire apparaître les traits de construction.
4-b- Sur ce graphique, graduer l’axe des abscisses en multiples de la demi-vie.

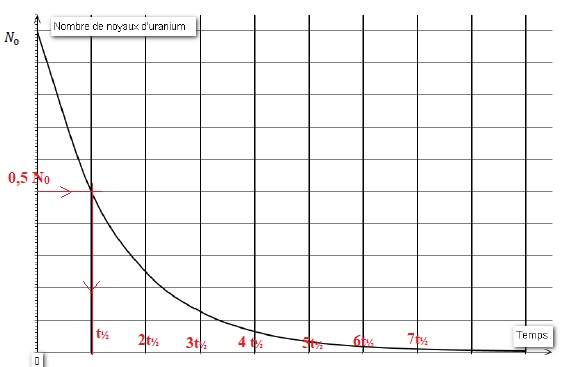
4-c- En utilisant ce graphique, estimer au bout de combien de demi-vies il ne reste plus que 1% des noyaux d’uranium 235 ? On notera sur la copie la bonne réponse parmi les trois suivantes, sans justifier.
Réponse A : entre 1 et 3 demi-vies
Réponse B : entre 3 et 5 demi-vies
Réponse C : entre 6 et 8 demi-vies. Vrai.
A t_½, il reste 50 % des noyaux d'uranium ; à 2t_½, il reste 25 % des noyaux d'uranium ; à 3t_½, il reste 12,5 % des noyaux d'uranium ;
à 4t_½, il reste 6,25 % des noyaux d'uranium ; à 5t_½, il reste 3,125 % des noyaux d'uranium ; à 6t_½, il reste 1,6 % des noyaux d'uranium ;
à 7t_½, il reste 0,80 % des noyaux d'uranium.
5- Sachant que la demi-vie t_½ de l’uranium 235 est de 0,704 milliard d’années, proposer une estimation de l’âge de la Terre.
6 x 0,704 =4,2 milliards d'années ; 8 x0,704 ~5,6 milliards d'années.