Des instruments, des notes et des gammes, enseignement scientifique, classe de première générale

Partie 1 : des instruments et des notes.
Les cordes d’un piano vibrent lorsqu’elles sont frappées par de petits marteaux actionnés par les touches du clavier. Les sons produits par le piano résultent de ces vibrations.
1- Calculer la fréquence associée au La4 située une octave au-dessus du La3.
La fréquence du La3 est f = 441 Hz.
La fréquence du La4 est : 2f = 2 x441 = 882 Hz.
2- On s’intéresse aux sons produits par ce piano. Un système d'acquisition informatisé permet l'enregistrement et la visualisation des signaux associés à ces sons.
Une graduation horizontale correspond à 1 ms.

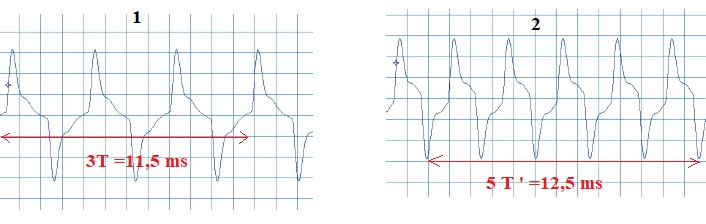
2-a- Justifier que les figures 1 et 2 correspondent à deux notes différentes.
2-b- Identifier les notes correspondantes aux figures 1 et 2.
Figure 1 : T = 11,5 / 3 10^-3 ~3,83 10^-3 s ; f = 1 /(3,83 10^-3) = 261 Hz ( Do3 : 262 Hz )
Figure 2 : T ' = 12,5 / 5 10^-3 ~2,5 10^-3 s ; f' = 1 /(2,5 10^-3) = 400 Hz ( sol3 : 393 Hz )

Partie 2 : des notes et des gammes.
La théorie musicale étant fondée sur des rapports de fréquences, on décide de simplifier les calculs en attribuant la valeur 1 (sans unité) à une fréquence choisie comme référence. Celle-ci correspond à une note de référence (par exemple 262 Hz pour le Do 3). On retrouve ensuite les fréquences réelles en multipliant les valeurs calculées par la fréquence de la note de référence.
La construction des gammes dites de Pythagore est basée sur le cycle des quintes : on part de la fréquence de valeur f₀ = 1. On construit une nouvelle fréquence, la quinte, en multipliant f₀ par 1,5. On réitère ce processus pour obtenir la quinte de la quinte, et ainsi de suite. À certaines étapes, le fait de multiplier par 1,5 une fréquence f comprise entre 1 et 2 peut donner une fréquence supérieure ou égale à 2. On se propose de démontrer que, si on divise par 2 la valeur obtenue, on la ramène dans l’octave.
3- On suppose que 1 ≤ f < 2 et on raisonne par disjonction de cas :
- premier cas : 1 ≤ f < 4 / 3. Montrer que 1 ≤ 1,5 f < 2.
On multiplie chaque terme par 1,5 : 1,5 ≤ 1,,5 f < 2.
1 <1,5 ≤ 1,,5 f < 2.
- deuxième cas : 4 / 3 ≤ f < 2. Montrer que 2 ≤ 1,5 f et 1 < 3 /4 f < 2.
On multiplie les deux premiers termes par 1,5 : 2 ≤ 1,5 f ;
On multiplie chaque terme par 3 / 4 : 1 < 3 / 4 f < 1,5 ; 1 < 3 / 4 f < 1,5 < 2.
4- L’algorithme suivant permet de calculer les fréquences des notes successivement obtenues par ce processus jusqu’à ce qu’on retombe sur la fréquence initiale.

Recopier et compléter le tableau ci-dessous en donnant les valeurs des 12 premières quintes obtenues par cet algorithme. Les résultats seront donnés d’abord sous forme exacte comme quotients d’une puissance de 2 par une puissance de 3, puis par leurs valeurs décimales approchées au centième obtenues à l’aide de la calculatrice.

n	0	1	2	3	4	5	6
f (fraction irréductible)	1	3 / 2	3² / 2³	3³ / 2⁴	3⁴ / 2⁶	3⁵/ 2⁷	3⁶/ 2⁹
f ( valeur approchée )	1	1,5	2,25 / 2 =1,13	1,69	2,53 / 2 =1,27	1,9	1,42
f > 2	faux	faux	vrai	faux	vrai	faux	faux
n	7	8	9	10	11	12
f (fraction irréductible)	3⁷/ 2¹¹	3⁸/ 2¹²	3⁹/ 2¹⁴	3¹⁰/ 2¹⁵	3¹¹/ 2¹⁷	3¹²/ 2¹⁹
f (valeur approchée)	2,14 / 2 = 1,07	1,60	2,40 / 2 = 1,20	1,80	1,35	2,025 / 2 = 1,01
f > 2	faux	faux	vrai	faux	faux	vrai