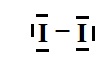Physique
chimie, synthèse du camphre au service du sportif, recycler un
médicament,
une onde un peu particulière, l'onde cobra.
E3C : enseignement de spécialité première générale.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
.
|
|
Synthèse
du camphre au service du sportif.
Le
baume du tigre est un onguent issu de la pharmacopée chinoise dont la
commercialisation remonte à la fin du XIXème siècle. En particulier, le
baume du tigre rouge est très utilisé pour soulager les douleurs
musculo-squelettiques ; il est donc particulièrement apprécié des
sportifs.
Le camphre constitue le principal composant du baume du tigre.
Historiquement, le camphre était d’origine naturelle : le plus
anciennement connu semble avoir été le camphre de Bornéo, fourni par un
grand arbre de l’île de Sumatra en Indonésie. Actuellement, la majorité
du camphre produit en France est obtenue par une synthèse multi-étapes
à partir de l’a-pinène
extrait de la résine de pin.
Cet exercice s’intéresse à la dernière étape qui permet de produire le
camphre par oxydation du bornéol avec comme oxydant l’acide chromique
(réactif de Jones). La transformation chimique peut être modélisée par
la réaction chimique d’équation :
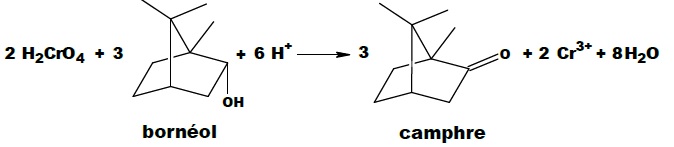
Étape 1. Dans un ballon bicol de 250 mL, placé dans un bain de glace,
muni d’une agitation magnétique, d’un réfrigérant à eau et d’une
ampoule de coulée, dissoudre 5,0 g de bornéol commercial dans 15 mL de
propanone. Ajouter goutte à goutte 11,0 mL de solution d’acide
chromique de concentration C = 2,0 mol·L-1. Enlever le bain
de glace et attendre que la température du
mélange atteigne la température ambiante.
Étape 2. Introduire le mélange dans une ampoule à décanter de 250 mL
contenant 120 mL d’eau et ajouter 25 mL d'éther diéthylique. Agiter,
décanter et séparer la phase organique. Traiter deux fois la phase
aqueuse avec chaque fois 25 mL d'éther diéthylique.
Étape 3. Regrouper et laver les phases organiques avec successivement
25 mL d'une solution saturée de chlorure de sodium (Na+
(aq) + Cl- (aq)), 25 mL d'une solution saturée
d'hydrogénocarbonate de sodium (Na+(aq) + HCO3−
(aq)) et 25 mL d'une
solution saturée de chlorure de sodium. Recueillir la phase organique
dans un erlenmeyer. Sécher sur sulfate de magnésium anhydre. Éliminer
le solvant grâce à un montage de distillation simple. Verser le résidu
du ballon dans bécher taré, refroidir et recueillir les cristaux
obtenus, les sécher.
Étape 4. Déterminer la masse puis réaliser le spectre infrarouge
du solide obtenu.
1. Indiquer, en
justifiant, les précautions à prendre lors de cette étape de la
synthèse.
L'acide chromique est cancérogène, dangereux pour l'environnement,
corrosif ; la propanone est inflammable.
Port de blouse, gants et lunette de protection. Travail sous hotte
aspirante, loin de toute flamme. Ne rien verser à l'évier.
2. Caractériser
chacune des étapes du protocole en utilisant les termes suivants :
analyse du
produit synthétisé ; transformation des réactifs ; isolement du produit
synthétisé.
Etape 1 : transformation des réactifs.
Etapes 2 et 3 : isolement du produit de la synthèse
Etape 4 : analyse du produit de la synthèse.
3. Justifier
l’utilisation de l’éther diéthylique dans l’étape 2 du protocole.
Le camphre est soluble dans l'éther diéthylique et peu soluble dans
l'eau. L'eau et l'éther diéthylique ne sont pas miscibles.
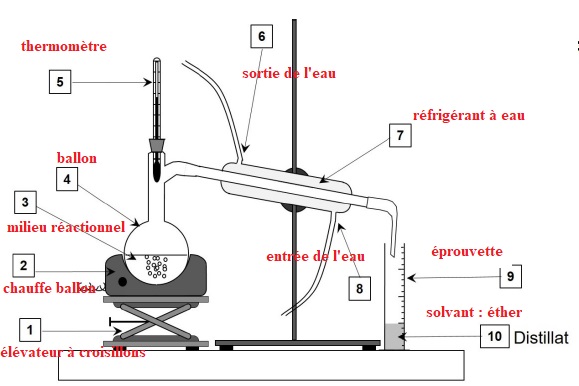
Le schéma du montage de distillation simple est donné ci-dessous.
4. Sans reproduire
le schéma, indiquer sur votre copie chaque nombre de la légende ainsi
que le terme associé. Préciser quelle(s) espèce(s) chimique(s)
est(sont) présente(s) dans le distillat (10).
5. À l’aide des
couples d’oxydo-réduction : H2CrO4 / Cr3+
et camphre / bornéol, retrouver l’équation de la réaction de synthèse
et justifier que le bornéol subit bien une oxydation.
Réduction de l'oxydant : 2 fois { H2CrO4
aq + 3e- +6H+aq --> Cr3+ aq + 4H2O
}
Oxydation du bornéol, réducteur qui cède 2 électrons : 3 fois { C10H18
O --> C10H16
O +2H+aq + 2e- }.
2H2CrO4
aq + 6e- +12H+aq +3 C10H18 O --> 2Cr3+ aq + 8H2O
+ 3C10H16
O +6H+aq + 6e-
Simplifier : 2H2CrO4 aq +6H+aq
+3 C10H18
O -->
2Cr3+ aq + 8H2O + 3C10H16
O.
6. Montrer que l’acide chromique et
le bornéol ont été introduits dns les propositions stoechiométriques.
n(bornéol) = 5,0 / M(bornéol) = 5,0 / 154,2 =0,033 mol.
n(acide chromique) = C V = 2,0 x0,011 = 0,022 mol.
2 moles d'acide chromique réagissent avec 3 moles de bornéol.
0,022 mole d'acide chromique réagissent
avec 1,5 x0,022 ~0,033 mole de bornéol.
Les réactifs sont en proportions stoechiométriques.
7. Montrer que la masse maximale de
camphre que l’on peut former à l’issue de la synthèse vaut mthéorique
= 5,0 g.
On peut espérer obtenir au mieux 0,033 mol de camphre soit 0,033 x
M(camphre) = 0,033 x152,2 ~5,0 g.
Une synthèse réalisée au laboratoire en suivant ce protocole a permis
d’obtenir 2,2 g de solide.
8. En supposant que
le solide obtenu est du camphre pur, déterminer le rendement de cette
synthèse.
masse réelle / masse théorique = 2,2 / 5 = 0,44 (44 %).
Lors de la synthèse au laboratoire, le technicien a réalisé une
chromatographie sur couche mince. Il a noté sur son cahier de
laboratoire :
Rf(camphre) = 0,52 attendu dans les conditions de la CCM et
il a reproduit le chromatogramme obtenu après élution et
révélation.
9. Analyser
l’allure du chromatogramme obtenu et indiquer les informations qu’il
fournit sur la synthèse.
 |
1. Prélèvement au début de la
transformation
2. Prélèvement en cours de transformation
3. Prélèvement en fin de transformation.
1. bornéol
2. bornéol et camphre
3. camphre
|
Le produit de la synthèse, après purification est du camphre.
Le spectre IR du bornéol commercial est fourni ci-dessous. Il
représente la transmittance (en %) en fonction du nombre d’onde
(wavenumbers en anglais) exprimé en cm-1.
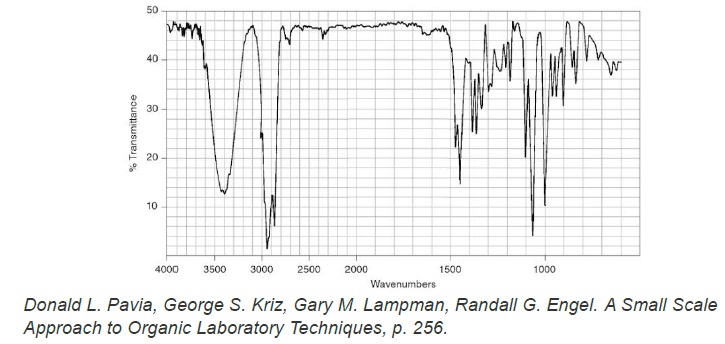
10. Donner les
principales modifications attendues sur le spectre IR du solide obtenu
par rapport celui du bornéol si le solide est du camphre pur.
Apparition d'une bande forte vers 1700 cm-1 (
caractéristique de la liaison C=O cétone).
Disparition de la bande liée à O-H liée vers 3100 - 3500 cm-1
ainsi que de la bande forte ( liaison C-O) vers 1050 - 1450 cm-1.
|
|
Recycler
un médicament.
La
Bétadine est un antiseptique local très utilisé dans les établissements
de santé et médicosociaux qui se périme rapidement après son ouverture.
Ce médicament est constitué d’une solution aqueuse de diiode, soluté
toxique pour les organismes aquatiques.
Cet exercice s’intéresse à l’extraction du diiode pour envisager
ensuite son rejet ou son recyclage.
1. Extraction
liquide-liquide du diiode.
1.1. Justifier, à
l’aide de deux arguments, le choix du solvant à utiliser pour extraire
le diiode contenu dans la solution de Bétadine®.
Le diiode est très soluble dans l'éthanol, mais l'éthanol est miscible
avec l'eau.
Le diiode est soluble dans le cyclohexane et ce dernier est non
miscible avec l'eau.
On choisira donc le cyclohexane.
1.2.Le schéma de
Lewis de la molécule de diiode est le même que celui du dichlore.
Représenter ce schéma de Lewis.
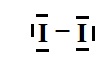
1.3.La molécule de
diiode I2 est-elle polaire ? En déduire une propriété du
solvant choisi précédemment.
La molécule de diiode n'est pas polaire ; il en est de même du
cyclohexane.
1.4. On utilise 20
mL de ce solvant pour extraire le diiode de 10 mL de solution de
Bétadine®. Quelle est la masse de solvant d’extraction utilisé ?
Masse volumique du cyclohexane : 0,78 g / mL.
Masse de solvant : 20 x 0,78 = 15,6 g.
1.5. Schématiser
les étapes du protocole expérimental d’extraction liquide-liquide
simple du diiode de 10 mL de solution de Bétadine® en tenant compte des
risques liés à l’utilisation du solvant choisi. Légender en précisant
les contenus des différentes phases.
Le cyclohexane est cancérogène, dangereux
pour l'environnement..
Port de blouse, gants et lunette de protection. Travail sous hotte
aspirante. Ne rien verser à l'évier.
Introduire dans une ampoule à décanter 20 mL de solvant et 10 mL de
bétadine.
Boucher et agiter. Laisser reposer.
La phase organique la moins dense, occupe la partie supérieure.
Retirer le bouchon et éliminer la phase aqueuse ( partie inférieure).
2. Comparaison de deux protocoles
d’extraction du diiode d’une solution aqueuse
On souhaite à présent comparer l’efficacité de deux méthodes
d’extraction du diiode d’une solution aqueuse, dont le principe est
décrit ci-dessous. Toutefois la solution aqueuse de diiode étant très
concentrée, on la dilue 10 fois, on obtient alors une solution S’.
- Méthode 1 : extraction simple
On procède à une extraction simple en utilisant un volume VS
= 20 mL de solvant pour 10 mL de solution de S’.
- Méthode 2 : extraction multiple
On procède à une première extraction en utilisant un volume VS1
= 10 mL de solvant pour 10 mL de solution de S’. On récupère la phase
aqueuse dans un bécher et on réalise une nouvelle extraction avec à
nouveau VS2 = 10 mL de solvant.
2.1.Déterminer la
couleur de la solution aqueuse de diiode.
Cette solution présente un maximum d'absorption vers 480 - 500 nm (
bleu vert ). La solution de diiode a la teinte complémentaire du bleu
vert, c'est à dire l'orangé.
2.2.A quelle
longueur d’onde faut-il régler le spectrophotomètre, pour mesurer
l’absorbance des solutions de diiode ? Justifier.
Pour un maximum de précision, on chosit une longueur d'onde
correspondnt au maximum d'absorption ( 480 - 500 nm).
Le spectrophotomètre est réglé, non pas sur la longueur d’onde trouvée
précédemment mais à une longueur d'onde λ = 600 nm : ce choix
exceptionnel permet de ne pas dépasser les limites de mesure du
spectrophotomètre. On trace l’évolution de l’absorbance du diiode en
solution
aqueuse en fonction de sa concentration en quantité de matière ; le
graphe représentant cette évolution est donné. Puis, on mesure les
absorbances des phases aqueuse finales obtenues à l’issue des deux
méthodes d’extraction.
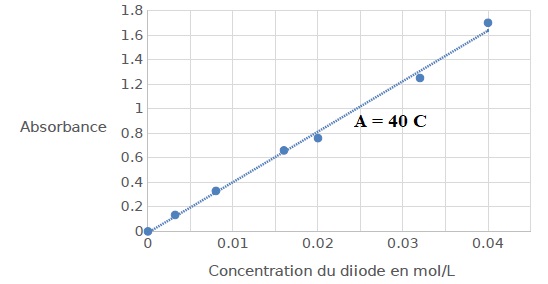
2.3. Quelle est la
loi vérifiée à l’aide de la courbe représentant l’évolution de
l’absorbance avec la concentration ?
La courbe est une droite passant par l'origine. La loi de Beer-Lambert
est vérifiée.
2.4. Quel type de
dosage permet-elle d’envisager ?
Dosage utilisant une méthode spectrophotométrique.
2.5.La mesure de
l’absorbance de la phase aqueuse finale, obtenue à l’issue des deux
méthodes d’extraction donne pour la méthode 1, A1 = 0,65 et
pour la méthode 2, A2 = 0,50. Comparer l’efficacité des deux
méthodes d’extraction.
Concentration du diiode dans l'eau ( méthode 1) : 0,65 / 40 = 0,016 mol
/ L.
Concentration du
diiode dans l'eau ( méthode 2) : 0,50 / 40 = 0,0125 mol / L.
La méthode 2 est la plus efficace, la concentration résiduelle du
diiode dans l'eau est plus faible.
2.6.La
fiche de sécurité du diiode indique que la concentration maximale d’une
solution aqueuse de diiode pour qu’elle soit sans effet sur
l’environnement est de 11 mg /L. Peut-on rejeter la phase aqueuse à
l’évier à l’issue d’une des deux méthodes d’extraction ? Commenter.
0,0125 M(diiode) = 0,0125 x 254 ~3,2 g / L.
Cette valeur est supérieure à 11 mg / L. La solution ne peut pas être
jetée à l'évier.
|
Une onde
un peu particulière : l'onde cobra.
Le cobra est un serpent qui a la capacité de se redresser. C’est en
référence à cette position que le jeu étudié ici a été nommé « onde
cobra ». Il ressemble à ce jeu dans
lequel on aligne des milliers de dominos pour ensuite les faire tomber
en cascade.
Il s’agit ici d’entremêler en une succession de losanges des bâtonnets
de bois, par exemple des bâtonnets de glace, pour constituer un long
croisillon horizontal puis d’en lâcher une
extrémité. L’assemblage se soulève alors, se redresse telle une tête de
cobra, en éjectant un à un les bâtonnets et en détruisant donc le
croisillon.

Pour constituer le croisillon, les bâtonnets se déforment avec des
fléchissements qui sont de l’ordre de leur épaisseur, mais qui
retrouvent leur forme initiale une fois libérés. Initialement, ils
stockent ainsi non pas de l’énergie potentielle de pesanteur mais de
l’énergie potentielle élastique. Des chercheurs ont montré que l’onde
cobra résultait d’une propulsion par réaction, dans laquelle le «
carburant » est cette énergie potentielle élastique stockée dans les
déformations des bâtonnets et la propagation est assurée par leur
éjection.
L’objectif de cet exercice est de déterminer la célérité de l’onde
cobra, d’étudier l’influence de la forme du croisillon sur la célérité
ainsi que de mener une analyse énergétique pour interpréter
l’onde cobra et prévoir la hauteur maximale des bâtonnets lors de la
propagation.
Sources : journal Le Monde (21 août 2017), journal Pour la Science
(n°490, août 2018).
Analyse ondulatoire.
1. Indiquer la
nature périodique ou non périodique de « l’onde cobra ».
Ce n'est pas une onde périodique : l’assemblage se soulève en éjectant un à
un les bâtonnets et
en détruisant donc le croisillon.
2. On souhaite décrire l’évolution
de la hauteur du centre de masse d’un bâtonnet au cours du temps (la
hauteur est nulle lorsque le bâtonnet est au sol). Le bâtonnet décrit
est figuré en
noir à l’instant t1 sur la figure 1, lorsqu’il est encore au
sol, et on peut considérer que son mouvement ultérieur est
approximativement vertical. Quatre représentations graphiques sont
proposées ci-dessous.
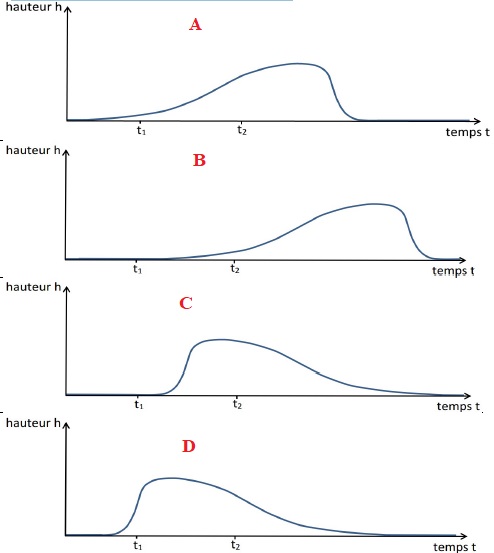
2.1. Parmi les
représentations graphiques proposées, éliminer la (ou les)
représentation(s) qui ne rend(ent) pas compte de la position du
bâtonnet à l’instant t1.
A l'instant t1, le bâtonnet est au sol : les représentations
A et D ne conviennent pas.
2.2. Parmi les
représentations restantes, choisir la représentation graphique qui
paraît la plus adaptée. On justifiera clairement le choix.
A l'instant t2, le bâtonnet atteint sa hauteur maximale : la
représentation C convient.
Des chercheurs ont réalisé des photographies successives de la
structure se soulevant au cours du temps. Quatre photographies
successives sont fournies sur la figure 4 ci-dessous. Le
croisillon a été réalisé avec des bâtonnets de longueur 11,4 cm et un
pas voisin de 5 cm (ce qui correspond à des bâtonnets disposés
perpendiculairement les uns par rapport aux autres ). L’échelle
verticale et l’échelle horizontale ne sont pas les mêmes.
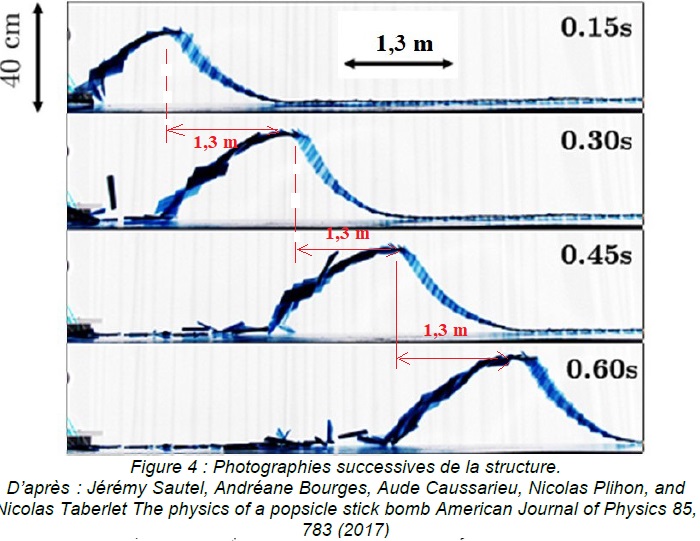
3. À l’aide de la
figure 4, justifier sans calcul que la célérité de l’onde cobra semble
approximativement constante.
4. Déterminer la
valeur de la célérité de l’onde cobra. On explicitera clairement la
méthode.
Le front d'onde avance de 1,3 m toutes les 0,15 s.
Célérité : c = 1,3 / 0,15 ~8,7 m /s.
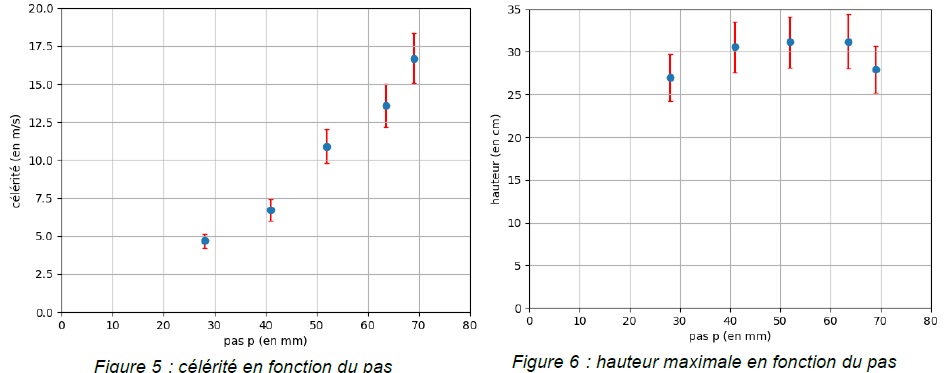
L’évolution de la célérité de l’onde et de la hauteur maximale atteinte
par chaque bâtonnet en fonction du pas sont reproduites ci-dessous
(pour des bâtonnets de longueur 11,4 cm). Les
barres indiquent l’incertitude-type pour chaque mesure.
5. Indiquer comment
on a intérêt à déformer le croisillon afin d’augmenter la vitesse par
rapport à la situation étudiée aux questions 3 et 4. On pourra faire un
schéma.
La célérité augmente quand le pas croît. La célérité passe de 5,0 m /s
pour un pas de 30 mm à près de 17 m /s pour un pas de 70 mm.
Le pas noté p est la distance entre deux sommets consécutifs sur un des
bords du croisillon. Augmenter la distance entre deux sommets
consécutifs sur un bord du croisillon revient à faire croître la
célérité.
6. Indiquer en
argumentant avec précision si la forme du croisillon a une influence
sur la hauteur atteinte par les bâtonnets.
Pour un pas compris entre 40 mm et 65 mm, la hauteur maximale atteinte
est constante.
Si p ~30 mm ou si p ~70 mm, la hauteur maximale atteinte est un
peu plus faible.
Analyse énergétique.
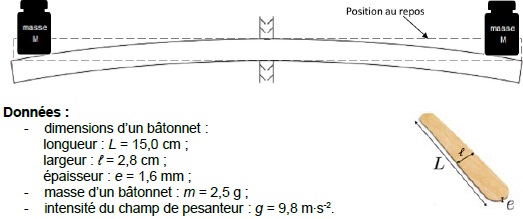
On souhaite estimer l’énergie nécessaire à la déformation d’un bâtonnet
dont les caractéristiques sont données ci-dessous. Pour ceci, on étudie
la situation suivante où on pose deux masselottes identiques à chaque
extrémité d’un bâtonnet fixé en son centre. Celui-ci se courbe et
stocke de l’énergie potentielle élastique. On note M la masse de
chacune des masselottes pour que les extrémités du bâtonnet descendent
d’une hauteur égale à son épaisseur. Pour déformer à ses deux
extrémités le bâtonnet décrit dans les données, on observe
expérimentalement qu’il faudrait que les masselottes aient chacune une
masse M environ égale à 100 g.
7. Exprimer le
travail du poids d’une masselotte durant sa descente. Calculer sa
valeur.
Chaque masselotte descend d'environ l'épaisseur e, soit 1,6 10-3
m.
Le travail du poids est moteur en descente.
W = M g e = 0,100 x 9,8 x 1,6 10-3 =1,568 10-3 J
~1,6 mJ.
On suppose que l’énergie transférée par travail mécanique est
entièrement stockée par le bâtonnet sous forme d’énergie potentielle
élastique.
8. En déduire la
valeur de l’énergie potentielle élastique d’un bâtonnet qui serait
déformé de cette façon par les deux masselottes avec un fléchissement
égal à son épaisseur à
chaque extrémité.
1,568 10-3 x2 ~3,1 mJ.
En pratique, puisque chaque bâtonnet est déformé en quatre points,
l’énergie potentielle stockée par bâtonnet est bien plus grande et vaut
approximativement 50 mJ.
L’énergie mécanique d’un bâtonnet est la somme de son énergie
cinétique, de son énergie potentielle de pesanteur (considérée nulle
lorsque le bâtonnet est au sol) et de son énergie
potentielle élastique (nulle lorsque le bâtonnet n’est pas déformé).
Lors de la propagation de l’onde, chaque bâtonnet est propulsé vers le
haut et n’est plus déformé. Lorsqu’il atteint sa
hauteur maximale, on peut considérer sa vitesse comme nulle.
9. En exploitant la
conservation de l’énergie mécanique pour un bâtonnet donné, exprimer
puis calculer la valeur de la hauteur maximale théorique atteinte par
chaque bâtonnet.
L'énergie mécanique initiale ( bâtonnet déformé immobile au sol ) est
sous forme potentielle élastique : 50 mJ.
L'énergie mécanique finale ( bâtonnet non déformé ayant atteint
l'altitude maximale ) est sous forme potentielle de pesanteur : m g hmax.
L'énergie mécanique se conserve : hmax = 50 / (mg) =50 /
(2,5 x9,8) ~2,0 m.
Lors de la propagation observée expérimentalement, la hauteur atteinte
par chaque bâtonnet est comprise entre 25 et 35 cm.
10. Proposer une
interprétation de la différence avec la valeur calculée précédemment.
Le bâtonnet n'est pas projeté verticalement mais de manière oblique ;
au point le plus haut le bâtonnet possède une vitesse horizontale non
nulle et donc de l'énergie cinétique.
Seule la composante verticale de la vitesse est nulle au point le plus
haut.
|
|
|