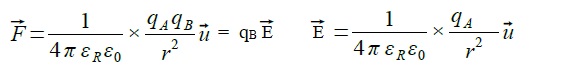Physique
chimie, le train à grande vitesse, construire un record, photopile et
développement durable,
plongée en eau douce.
E3C : enseignement de spécialité première générale.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
.
|
|
Le train
à grande vitesse, construire un record.
Le
dernier record du monde de vitesse sur rail du TGV (Train à Grande
Vitesse) a été homologué le 3 avril 2007. Une rame expérimentale a
atteint à 13h14 la vitesse de 574,8 km·h−1 sur la toute
nouvelle ligne Est européenne.
Le mur de la caténaire.
L’alimentation des moteurs électriques du TGV est réalisée à l’aide de
la caténaire et du pantographe.
La caténaire est le câble électrique tendu au-dessus des voies. Le
pantographe est le dispositif articulé fixé sur le toit de la
locomotive, permettant une liaison électrique par frottement sur la
caténaire.
Le pantographe appuie sur le câble et le soulève, créant une
déformation en forme de V inversé. Lorsque le train se déplace, une
onde mécanique progressive se propage dans la caténaire devant la
locomotive. Si le train rattrape l’onde, le contact entre le
pantographe et la caténaire est rompu et la puissance électrique
transmise aux moteurs diminue. La célérité de l’onde dans la caténaire
est une contrainte qui limite la vitesse du train, on parle d’un « mur
de la caténaire » par analogie avec le mur du son.
1. L’onde qui se
propage dans la caténaire est progressive et mécanique. Rappeler la
définition d’une onde progressive puis indiquer ce qui permet de la
qualifier de mécanique.
Une onde progressive mécanique est la propagation d'une perturbation
dans un milieu matériel avec transport d'énergie, sans transport de
matière. L'onde mécanique a besoin d'un milieu matériel pour se
propager ; elle ne se propage pas dans le vide.
Un système de poulies et de contrepoids permet de tendre plus ou moins
la caténaire. Pour étudier l’influence de cette tension mécanique T (en
Newton), on utilise un logiciel de simulation mis en ligne par
l’université du Colorado. Dans cette simulation la caténaire du train
est modélisée par la corde sur laquelle se propage une perturbation.
Deux captures d’écran de ce logiciel sont données ci-dessous.
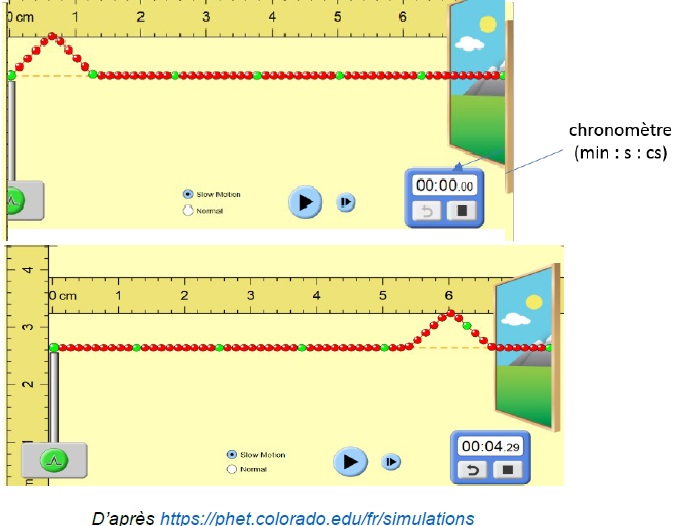
2. Déterminer, à
l’aide des deux captures ci-dessus la valeur de la vitesse de
propagation de l’onde dans la simulation.
L'onde progresse de 5,4 cm en 4,29 s.
c = 5,4 10-2 / 4,29 =1,26 10-2 m /s.
3. Une deuxième
simulation avec une valeur de tension plus élevée du câble donne une
célérité de 6,3×10-2 m·s-1. Indiquer l’influence
du paramètre tension sur la célérité de l’onde.
La célérité et la tension varient dans le même sens. Quand l'une croît,
l'autre augmente également.
L’expression littérale de la célérité de l’onde mécanique qui se
propage dans la caténaire est :
c=( T / ( ρ. S))½.
avec : c la célérité de l’onde en mètres par seconde (m·s-1)
;
T la tension exercée sur la caténaire en Newton (N) ;
S la section de la caténaire (m2) ;
ρ la masse volumique du matériau constitutif du câble (kg·m−3).
La SNCF a spécifié que pour des trajets commerciaux, la vitesse de ses
TGV ne devait pas dépasser 70 % de la vitesse de propagation des ondes
dans la caténaire.
Nous disposons des informations suivantes sur les caténaires utilisées :
T = 2,6 104 N ; S = 150 mm2 ; r = 8920 kg m-3.
4. Vérifier la
cohérence de cette relation avec les résultats obtenus lors de la
simulation.
La célérité est proportionnelle à la racine carrée de la tension.
Célérité et tension varient bien dans le même sens. Cette relation est
cohérente avec les résultats de la simulation.
5. Déterminer, en
m·s−1 puis en km·h-1, la valeur de la vitesse
théorique maximale que ne doit pas dépasser un TGV en exploitation
commerciale.
c = (2,6 104 / (8920 x150 10-6))½
=1,4 102 m /s soit 1,4 102 x3,6 = 5,0 102
km / h.
Vitesse maximale du train : 5,0 102 x 0,70 = 3,5 102 km
/ h ( ~ 98 m /s).
6.
Proposer une argumentation d’une dizaine de lignes en indiquant sur
quels paramètres les ingénieurs ont pu agir pour repousser le mur de la
caténaire et ainsi faire franchir au TGV la barre symbolique des 500
km·h−1.
On précisera dans le raisonnement les paramètres modifiés, le sens
d’évolution de leurs valeurs (plus élevée ou plus faible) ainsi que le
choix le plus approprié et le plus économique.
Le cuivre étant le meilleur conducteur de l'électricité, il faut
conserver ce métal ( L'argent est meilleur conducteur électrique que le
cuivre, mais il est plus cher et ne possède pas les mêmes propriétés
mécaniques ).
Diminuer la section S du câble : on risque la rupture si la tension
croît ; de plus la résistance électrique va augmenter et en
conséquence les pertes par effet Joule.
La solution la plus judicieuse est d'augmenter la tension du câble.
Freinage d’urgence et
distance de freinage.
Un TGV commercial de masse M = 425 t roulant à la vitesse v0
= 320 km·h−1
sur une voie que l’on supposera rectiligne et horizontale doit
effectuer un arrêt d’urgence. La valeur de la distance nécessaire pour
que le TGV s’immobilise (distance d’arrêt) est de 3,2 km.
Au cours d’un essai dans la phase de préparation du record, un incident
a déclenché le freinage d’urgence et la rame expérimentale (de masse M’
= 270 t roulant à la vitesse v1 = 501,6 km·h−1)
s’est immobilisée au bout de 15 km.
7. À l’aide d’une
approche énergétique, justifier le sens de l’évolution de cette
distance d’arrêt.
L'énergie cinétique initiale est proportionnelle au carré de la vitesse
; cette énergie est dissipée sous forme thermique lors du freinage. La
vitesse passe de 320 à 501,6 km /h ( la vitesse croît d'un facteur 1,6
et le carré de la vitesse croît d'un facteur 1,62 ~2,5).
M' = 0,64 M ; l'énergie cinétique de la rame expérimentale croît
de 2,5 x0,64 ~1,6.
La distance d'arrêt va donc croître.
Alimentation électrique
des moteurs.
Pour fournir plus de puissance aux moteurs électriques de la rame, la
tension électrique de la caténaire a été portée à 31 kV contre 25 kV en
temps normal. Lors des essais, la valeur de l’intensité du courant
traversant le pantographe est en moyenne égale à 800 A.
8. Calculer la
valeur de la puissance électrique fournie par la caténaire aux moteurs
électriques.
P = UI = 31 103 x 800 =2,48 107 W = 2,48 104
kW.
La puissance restituée par l’ensemble des moteurs a été estimée à 19
600 kW (soit plus du double de celle d’une rame de TGV classique).
9. Recopier et
compléter le schéma suivant qui représente le bilan de puissance des
moteurs de la rame.

10. Exprimer et
calculer le rendement de l’ensemble des moteurs de la rame
expérimentale. Expliquer pourquoi il ne peut être supérieur à 1.
Un rendement est toujours inférieur à 1, une partie de l'énergie reçue
est dissipée en énergie thermique.
Rendement : 19 600 / (2,48 104) =0,79 ( 79 %).
|
|
Photopile
et développement durable.
On appelle « générateur photovoltaïque » un assemblage de modules (ou
panneaux) photovoltaïques, eux-mêmes composés de cellules
photovoltaïques nommées également photopiles.
https://www.futura-sciences.com/
PREMIÈRE PARTIE : étude de
la puissance électrique délivrée par une photopile.
Une photopile fonctionne comme un générateur réel, c’est-à-dire qu’elle
peut être modélisée par une source idéale de tension placée en série
avec une résistance. On la représente par le symbole de la pile avec
deux flèches pointant vers le dipôle ; ces flèches symbolisent la
lumière.
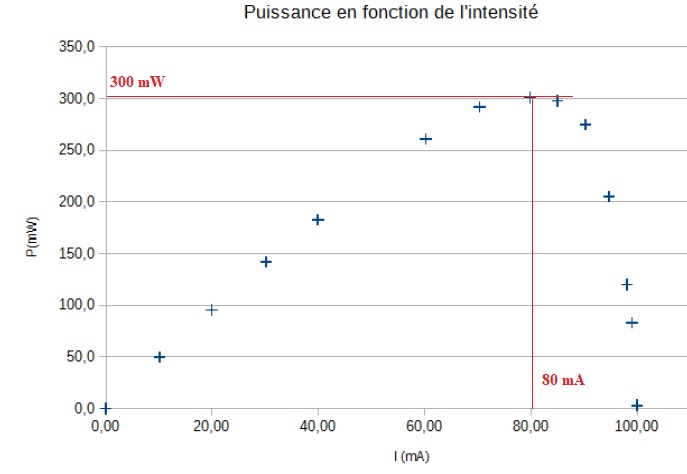
On désire tracer la courbe donnant les variations de la valeur de la
puissance électrique produite par une photopile en fonction de celle de
l’intensité du courant qu’elle débite.
On dispose du matériel suivant : photopile, voltmètre, ampèremètre,
interrupteur (noté K), fils de connexion, boîte de résistance réglable
et lampe de forte intensité. La lampe sert à éclairer la photopile avec
un éclairement constant : la puissance lumineuse qui arrive sur la
photopile est toujours la même au cours de l’expérience ; elle vaut Plum
= 3,0 W.
1. Quelle est la
conversion d’énergie réalisée par une photopile ?
L'énergie lumineuse est convertie partiellement en énergie électrique ;
une autre partie est dissipée en énergie thermique.
Le montage expérimental nécessaire à l’étude est mis en place. Son
schéma, représenté ci-dessous.
2. Compléter avec
l’emplacement du voltmètre et de l’ampèremètre. Le symbole normalisé de
l’ampèremètre est A et celui du voltmètre est V.
On précisera aussi les positions des bornes « COM » de chaque appareil
pour assurer la lecture d’une valeur positive.
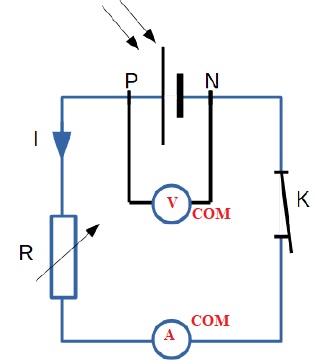
3. Comment faire
varier la valeur de l’intensité I du courant dans le circuit ?
Modifier la résistance électrique du circuit à l'aide du rhéostat.
L’évolution de la puissance électrique produite par la photopile en
fonction de l’intensité du courant qu’elle débite a été tracée à partir
de ces valeurs expérimentales.
Déterminer, par le calcul, la valeur manquante dans le tableau.
I = 50,0 mA ; UPN = 4,50 V ; Pél =50,0 x 4,50 =
225 mW.
4. Expliquer
pourquoi il n’est pas souhaitable que la photopile délivre son courant
maximal.
Pour Imax = 100 mA, UPN = 0,030 V et Pél
= 3,0 mW, valeur très inférieure à Pél max.
5. Pour quelle
valeur de l’intensité du courant la puissance délivrée par la photopile
est-elle maximale ? Que vaut alors cette puissance ? Justifier
graphiquement la réponse.
La puissance électrique est maximale pour I = 80 mA.
6. Définir puis
évaluer le rendement, noté η.
Rendement = puissance électrique fournie / puissance lumineuse reçue =
0,300 / 3,0 = 0,10 ( 10 %).
7. Formuler deux
raisons pour lesquelles ce rendement n’est pas égal à 1.
Seuls un petit nombre de photons possèdent assez d'énergie pour
arracher un électron du silicium et créé un courant électrique.
Une partie de la puissance électrique est convertie en chaleur par
effet Joule.
DEUXIÈME PARTIE :
utilisation de la photopile pour l’alimentation électrique d’un
appartement.
L’éclairement en France.
La puissance lumineuse reçue sur la Terre en provenance du Soleil
dépend de l’endroit où l’on se trouve sur la planète, de la saison,
ainsi que des conditions météorologiques. La consommation moyenne en
chauffage électrique d’un appartement thermiquement bien isolé est
voisine de 5.103 kWh par an.
L’étude porte sur un immeuble de 6 appartements thermiquement bien
isolés, situé à Valence, dans le sud-est de la France ( 1530 kWh / m2
/ an ). Sur le toit de l’immeuble est installé un dispositif de
panneaux photovoltaïques recouvrant totalement une surface d’aire Spanneaux
= 100 m². Ces panneaux sont confectionnés avec des photopiles
identiques à celle étudiée ci-dessus ; ils fonctionnent au maximum de
la puissance délivrée.
8. Quel est le
nombre d’appartements de cet immeuble que cette installation de
panneaux photovoltaïques permet d’alimenter en électricité ?
Energie solaire
disponible : 1530 x 100 =1,53 105 kWh / an.
Energie électrique disponible : 1,53 105 x 0,10 = 1,53 104
kWh / an.
Nombre d'appartements :1,53 104 / (5 103) ~ 3.
En utilisant du silicium monocristallin, le rendement atteint 20 % ;
dans ce cas six appartements peuvent être alimentés.
9. En
utilisant les questions précédentes pour justifier vos affirmations,
expliquer pourquoi le photovoltaïque contribue à faire face au
réchauffement climatique, mais que cette technologie doit être associée
à d’autres sources d’énergie. La réponse attendue comportera moins de
dix lignes.
Dans le monde en 2020, près de 70 % de l'électricité est produite par
des centrales thermiques utilisant les combustibles fosilles, source de
dioxyde de carbone contribuant à l'effet de serre. Le soleil étant
abondant sur terre et étant une source d'énergie inépuisable, les
cellules photovoltaïques peuvent produire de l'électricité, sans
contribuer à l'effet de serre.
Mais c'est une source d'énergie intermittante. En cas de faible
consommation d'électricité et de fort ensoleillement, l'excès
d'électricité peut être utilisé :
- pour l'électrolyse de l'eau ; production de dihydrogène
alimentant des piles à combustible ;
- pomper l'eau d'un lac inférieur à un lac situé à une altitude
plus élevée ( cette eau sera turbinée en cas de manque de soleil
et de forte consommation électrique.
|
Plongée en eau douce.
1. Pression et profondeur.
Un plongeur débutant ressent souvent une douleur intense au niveau des
tympans lors des plongées. Le tympan est une membrane qui sépare
l’oreille moyenne du milieu extérieur. Il est
assimilable à un disque de surface S=6,0×10−5 m². Une légère
différence entre la pression extérieure et celle de l’air dans
l’oreille moyenne suffit à provoquer des douleurs qui peuvent aller
jusqu’à l’inflammation du tympan : c’est le barotraumatisme
auriculaire. Celui-ci peut se déclarer dès lors que la différence entre
la force pressante exercée par un fluide extérieur et celle exercée par
l'air intérieur sur le tympan excède une valeur de l’ordre de 2 N .
Pour l’éviter, il est possible d’effectuer la manoeuvre de Valsalva :
elle consiste à expirer tout en se pinçant les narines afin de
rééquilibrer les pressions de part et d’autre du tympan.
Un plongeur souhaite vérifier au laboratoire l'influence de la
profondeur sur la pression lors d'une séance de travaux pratiques. Pour
cela, il utilise un manomètre associé à un tuyau en
plastique pour mesurer la valeur de la pression, un mètre ruban pour
mesurer celle de la profondeur et un long tube de plexiglas.
Il remplit le tube de plexiglas avec de l'eau et y plonge le tuyau en
plastique. Il relève la pression P en fonction de la profondeur
d'immersion h de l'extrémité du tuyau.
h (cm)
|
0
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
P(hPa)
|
1012
|
1023
|
1032
|
1042
|
1052
|
1062
|
1072
|
1082
|
1091
|
P-P0 =P-1012 (hPa)
|
0
|
11
|
20
|
30
|
40
|
50
|
60
|
70
|
79
|
1.1. Expliquer qualitativement le lien entre la pression et le comportement microscopique des entités qui constituent le fluide.
Quand la pression augmente, les entités qui constituent le fluide sont
plus proches les unes des autres. Plus la pression est grande, plus les
chocs entre entités sont nombreux.
1.2. En utilisant
une étude graphique, tester la loi fondamentale de la statique des
fluides à partir des mesures consignées dans le tableau ci-dessus.

1.3. On considère que la loi fondamentale de la statique des fluides est vérifiée à 10 mètres de profondeur.
On considère que le plongeur effectue la descente de la surface de
l’eau jusqu’à 10 m de profondeur sans réaliser la manoeuvre de
Valsalva. Risque-t-il un barotraumatisme
auriculaire ?
Pression à cette profondeur : P -1,012 105 = reau g h= 1000 x9,8 x10 =9,8 104 Pa ; P = 1,99 105 ~2,0 105 Pa.
Force extérieure exercée sur le tympan : F = P S = 2,0 105 x 6,0 10-5 = 12 N.
Force exercée par l'air intérieur : 1,0 105 x 6,0 10-5 = 6 N.
La différence entre ces deux forces étant supérieure à 2 N, il risque un barotraumatisme auriculaire.
2. Le sens électrique chez les poissons.
Les poissons électriques.
On appelle poisson électrique les poissons capables d'utiliser un
courant électrique pour s'orienter, pour se protéger ou pour
communiquer.
Force et champ électrostatiques.
Un objet possédant une charge électrique qB placée dans un champ électrostatique E, engendré par une charge électrique qA, subit une action mécanique modélisée par une force
électrostatique donnée par la loi de Coulomb : 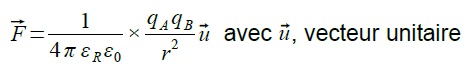
de même direction que la droite reliant les deux charges et orienté de A vers B, εR et ε0 deux constantes appelées permittivités diélectriques, qA et qB les charges, r la
distance entre les deux charges.
permittivité diélectrique du vide : ε0=8,85 10−12 F .m−1;
permittivité diélectrique relative de l'air par rapport au vide : εR=1,00 ;
permittivité diélectrique relative de l'eau par rapport au vide : εR=78,5.
Un plongeur se trouve à 2,0 m d'une anguille électrique. En première
approximation, on modélise une partie de l'anguille par un point placé
en A et de charge unique qA= 4,4×10-12 C.
2.1. Donner l’expression du champ électrostatique créé au point B par une charge qA.
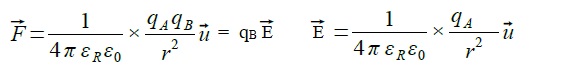
2.2. L’intensité du champ
électrostatique décroît très vite avec la distance. En outre, les
valeurs des champs électrostatiques créées par les poissons sont
souvent faibles car l’eau, par rapport à l’air, divise par environ 80
l’amplitude du champ électrostatique. Justifier ces deux affirmations.
Le carré de la distance intervient au dénominateur ; plus la distance est grande plus le champ électrique est faible.
La permittivité relative de l'eau est 80 fois plus grande que celle de l'air et la permittivité relative figure au dénominateur.
2.3. Dans le cadre
de cette modélisation, calculer la valeur du champ électrostatique
ressenti par le plongeur. Ce champ est-il perceptible par le plongeur ?
Justifier.
E = 4,4 10-12 / (4 x3,14 x80 x8,85 10-12 x 22) =9,9 10-3 V m-1.
Cette valeur est inférieure au seuil de perception ( 10 kV m-1), ce champ électrique n'est pas perceptible par le plongeur.
2.4. Le champ
électrostatique créé par un poisson électrique peut être assimilé à
celui d’un ensemble composé de deux charges électriques de signes
opposés.
On donne les lignes de champ électrostatique créé par un ensemble de deux charges électriques placées aux points M et N.
Pour chaque figure, donner le signe des charges placées aux points M et N.
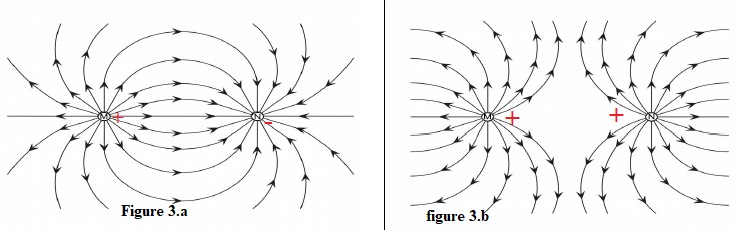
Parmi les deux figures proposées, laquelle correspond au modèle du poisson électrique ?
Le champ électrostatique créé par un
poisson électrique peut être assimilé à celui d’un ensemble composé de
deux charges électriques de signes opposés. Figure 3.a
|
|
|