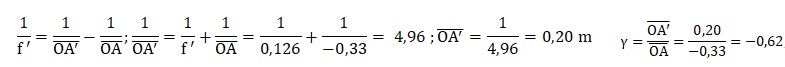Physique
chimie, ballon sonde, recyclage d'une solution de bouillie bordelaise,
photographie à l'aide d'une lentille boule.
E3C : enseignement de spécialité première générale.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
Ballon
sonde.
Dans le cadre d’un atelier scientifique, des lycéens ont conçu un
ballon-sonde constitué :
d’une enveloppe fermée remplie d’hélium ;
d’une nacelle contenant des appareils de mesure et un parachute.
Lors du lâcher, le ballon-sonde communique avec une station au sol. Des
mesures de pression, température, position sont récoltées au cours de
l’ascension.
L’objectif de cet exercice est de justifier le choix de valeur de la
fréquence de télécommunication et de confronter certaines mesures
réalisées à des modèles physiques.
1. Choix technique pour la
télécommunication.
Pour éviter les interférences avec d’autres systèmes, les lycéens
doivent respecter les normes en vigueur. Leur ballon-sonde doit émettre
des ondes électromagnétiques dans le domaine radioélectrique UHF (Ultra
Hautes Fréquences), que l’union internationale des télécommunications a
attribué au service de la météorologie.
Les lycéens ont choisi de régler la valeur de la fréquence d’émission
de leur ballon-sonde à f = 403,2 MHz.
1.1.Citer un autre
type d’ondes que les ondes électromagnétiques. En donner un exemple.
Les ondes mécaniques : ondes sonores, la houle.
1.2.Exprimer la
relation entre célérité c, longueur d’onde l et fréquence f.
l = c
/ f.
1.3.Déterminer la
valeur de la longueur d’onde des ondes émises par le ballon-sonde. Commenter
le choix effectué par les lycéens par rapport aux normes de
télécommunication.
3,00 108 /
(403,2 106) =0,744 m.
Cette valeur comprise entre 10 cm et 1 m appartient aux ondes UHF
attribuées à la météorologie.
2. Décollage du
ballon-sonde.
On considère le ballon juste après le décollage, étudié dans le
référentiel terrestre supposé galiléen. On néglige les frottements
exercés par l’air. Le système {ballon + nacelle + hélium} est soumis à
deux forces :
son poids, noté P ;
la poussée d’Archimède, notée F, verticale, dirigée vers le haut
telle que sa norme F = 50 N.
2.1.Calculer la
valeur de la masse m totale du système étudié.
masse totale = m = masse enveloppe + masse nacelle + masse hélium
= 0,32 +3,6 +0,70 = 4,62 kg ~4,6 kg.
2.2.Calculer la
valeur du poids du système {ballon + nacelle + hélium}.
P = m g = 4,62 x9,81 = 45,3 ~45 N.
2.3.Représenter les
forces exercées sur le système {ballon + nacelle + hélium} modélisé par
un point matériel noté S.
2.4.En déduire le
vecteur représentant la somme des forces appliquées sur le système et
donner les caractéristiques de ce vecteur (direction, sens, norme).
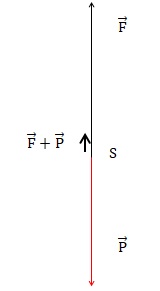
Le vecteur somme des forces est vertical, orienté vers le haut, de
norme 50-45 = 5 N.
Le ballon possède une trajectoire verticale ascendante. Les lycéens ont
calculé la vitesse du ballon-sonde à partir des mesures de positions.
La vitesse est V1 = 1,1 m.s-1 à t1 =
1,0 s et V3 = 3,2 m.s-1 à t3 = 3,0 s.
2.5. Calculer la
variation de la valeur de la vitesse entre les instants t1
et t3.
D v =
3,2 -1,1 = 2,1 m s-1.
2.6.Montrer que
cette variation est cohérente avec les caractéristiques de la somme des
forces appliquées sur le système.
Accélération a = Dv
/ Dt = 2,1 / 2 =
1,05 m s-2 ; m a = 4,6 x1,05 = 4,83 ~4,8 N.
Ecart relatif ( 5-4,8) / 5 = 0,04 ( 4 %). Les valeurs sont cohérentes.
3. Éclatement.
Dans cette partie, on considère que l’enveloppe du ballon-sonde est
parfaitement souple et extensible de sorte que la pression de l’hélium
à l’intérieur est constamment égale à la pression atmosphérique.
Relevé de la pression en fonction de l'altitude ( d'après Supélec ).
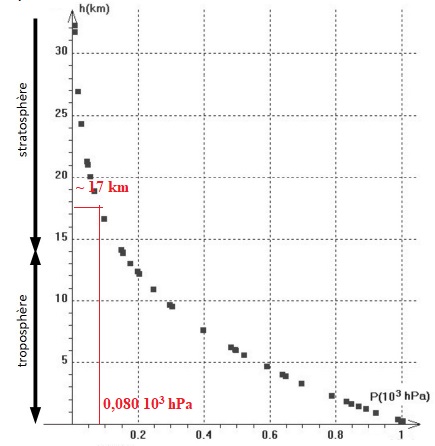
3.1.Expliquer
comment varie la pression dans le ballon sonde lorsque l’altitude
augmente.
La pression atmosphérique, donc la pression dans le ballon, diminue
avec l'altitude.
3.2. Énoncer la loi
de Mariotte relative au produit de la pression P par le volume V d’un
gaz pour une quantité de matière donnée et une température constante.
Pour une
quantité de matière donnée et une température constante, le produit de
la pression d'un gaz par son volume est constant..
3.3. À l’aide de la loi de Mariotte,
indiquer comment varie qualitativement le volume du ballon au cours de
son ascension. Déterminer ensuite l’altitude maximale atteinte par le
ballon au moment de l’éclatement.
Volume initial du ballon V0 = 4,0 m3 ; Patm
sol = 1,0 103 hPa.
V0 Patm
sol = Vh Ph = constante.
A l'altitude h, la pression est inférieure à la pression au niveau du
sol : le volume du ballon croît avec l'altitude.
3.4.En réalité le ballon a atteint
une altitude de 31 km, elle est supérieure à celle prévue dans la
question précédente. Proposer une explication.
4,0 x1,0 103
=V max P avec Vmax =51 m3.
P = 4,0 103 / 51 ~78 hPa ~ 0,08 103 hPa.
La température de l'atmosphère n'est pas constante ; cette température
varie selon l'altitude : la loi de Mariotte ne s'applique pas.
|
|
Recyclage
d'une solution de bouillie bordelaise.
Cette poudre est constituée de sulfate de cuivre hydraté CuSO4,5H2O(s)
et d’hydroxyde de calcium Ca(OH)2(s).
On obtient, par dissolution de cette poudre dans l’eau, une solution
contenant des ions cuivre Cu2+ à pulvériser sur les végétaux.
Le but de l’exercice est de déterminer si la solution de bouillie
bordelaise notée S, fabriquée en trop grande quantité par un jardinier
amateur, peut être jetée à l’évier ou doit être traitée ou recyclée.
1. Déterminer la
couleur de l’espèce ionique Cu2+(aq) en solution aqueuse.
Justifier.
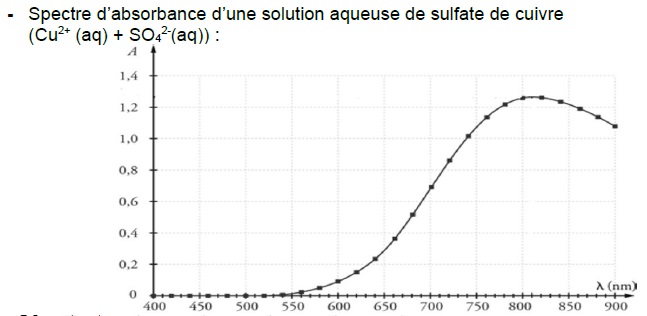
La solution de sulfate de cuivre présente un maximum d'absorption vers
750 nm- 800 nm ( rouge). La solution a la teinte complémentaire du
rouge, c'est à dire le bleu -vert.
On souhaite déterminer la concentration en quantité de matière d’ions
cuivre Cu2+(aq) de la solution de bouillie bordelaise S, par
un dosage spectrophotométrique. On réalise pour cela une gamme étalon
et des mesures d’absorbance à la longueur d’onde 810 nm.
2. Expliquer en
quelques lignes le principe de cette méthode de dosage.
On réalise des solutions de sulfate de cuivre de concentrations connues
et pour chaque solution, on mesure l'absorbance à 810 nm.
On trace la courbe donnant l'absorbance en fonction de la concentration.
On mesure l'absorbance de la solution de concentration inconnue de
sulfate de cuivre. Le graphe permet de trouver cette concentration.
On dispose d’une solution mère de sulfate de cuivre S0 de
concentration en quantité de matière d’ions cuivre Cu 2+(aq)
égale à C0 = 0,040 mol·L-1. À partir de cette
solution S0 on prépare différentes solutions Si.
Le volume de chaque solution fille obtenue est égal à V =10,0 mL.
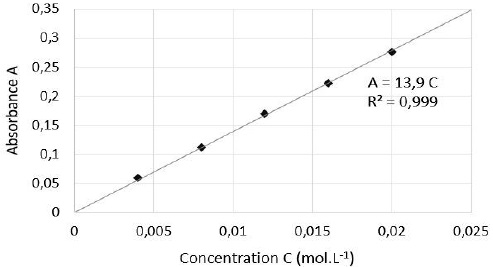
On mesure l’absorbance A des différentes solutions préparées et on
trace le graphique suivant :
4. Après avoir
rappelé l’expression de la loi de Beer-Lambert en indiquant le nom des
grandeurs et les unités associées, déterminer si les résultats
expérimentaux obtenus sont en accord avec cette loi.
A = k C ; A absorbance sans unité ; C : concentration en mol / L ; k :
coefficient de proportionnalité en L / mol.
Le graphe est une droite, en accord avec la loi de Beer-Lambert.
Afin de déterminer la concentration de la bouillie bordelaise préparée
par le jardinier, on dilue 20 fois la solution S avant de l’analyser
avec le spectrophotomètre. On mesure une absorbance A’ = 0,120 pour la
solution diluée S’.
5. Détailler le
protocole expérimental de préparation des 100 mL de la solution S’.
Prélever 5,0 mL de solution mère à l'aide d'une pipette jaugée de 5,0
mL.
Verser dans une fiole jaugée de volume 5,0 x20 = 100,0 mL.
Compléter avec de l'eau distillée jusqu'au trait de jauge.
Boucher et agiter pour rendre homogène.
6. Déterminer si le
jardinier peut rejeter son excédent de solution S à l’évier ou s’il
doit le faire recycler.
C' = 0,120 / 13,9 = 8,63 10-3 mol / L.
C = 20 C' = 20 x8,63 10-3 ~0,17 mol / L.
Concentration massique en ion Cu2+ :C m(Cu) = 0,17 x 63,5
~11 g / L.
Concentration en masse limite d’ions Cu2+ pour les rejets
dans les eaux usées : Cm = 0,5 mg par litre d’eau déversée.
Il faut donc recycler.
La toxicité de la bouillie bordelaise est liée à la présence des ions
cuivre Cu2+. Un traitement pour éliminer ces ions consiste à
ajouter des pastilles d’hydroxyde de sodium NaOH(s). La transformation
est modélisée par la réaction des ions cuivre Cu2+ présents
dans la bouillie bordelaise et des ions hydroxyde OH–
apportés par les pastilles d’hydroxyde de sodium) pour former un
précipité d’hydroxyde de cuivre Cu(OH)2(s) qui est récupéré
par filtration puis traité.
L’équation de la réaction chimique est la suivante :
Cu2+(aq) + 2 OH - (aq) → Cu(OH)2(s)
On souhaite traiter 500 mL d’une solution dont la concentration en
quantité de matière d’ions Cu2+ est égale à CT =
0,22 mol.L-1.
7. Déterminer la
masse m d’hydroxyde de sodium NaOH(s) à ajouter à cette solution pour
éliminer totalement les ions cuivre sans pour autant que les ions
hydroxyde ne soient en excès.
n(Cu2+) =0,500 x 0,22 = 0,11 mol.
n(NaOH) = 2 x0,11 = 0,22 mol.
Masse de soude : 0,22 M(soude) = 0,22 x40 = 8,8 g.
|
Photographie
à l'aide d'une lentille boule.
On
souhaite reproduire au laboratoire cette photographie insolite en
remplaçant la bulle d’eau par une lentille mince convergente (L) et en
utilisant un personnage en bois.
Afin de réaliser cette reproduction au laboratoire, on se propose de :
- modéliser la situation photographiée à bord de la station spatiale ;
- déterminer certains paramètres de la situation réalisée au laboratoire.
Détermination de la distance focale de la bulle d’eau
Pour reproduire cette expérience, il faut évaluer la valeur de la
distance focale d’une bulle d’eau qui constitue une lentille boule de
distance focale f’ = OF’ (en m) qui se comporte en première
approximation comme une lentille mince. Cette distance focale donnée par la relation :
f '=O F'= neau×R / (2×(neau−1) où n est l’indice
de réfraction du matériau constituant la lentille boule, R est son
rayon, O le centre de la lentille boule et F’ le foyer image de
celle-ci.
1. En considérant que la bulle d’eau possède un diamètre de l’ordre de 5 cm, déterminer la valeur de sa distance focale.( neau = 1,33).
f ' = 1,33 x 0,025 /(2x 0,33) =0,050 m = 5,0 cm.
Modélisation de la situation photographiée dans la station spatiale.
On considère qu’une bulle d’eau se comporte comme une lentille mince
convergente. La proposition de la modélisation de la situation à bord
de la station spatiale est donnée ci-après.
AB représente une petite partie du visage de l’astronaute et A’B’ est
l’image de AB à travers la lentille. Le schéma présente les éléments
principaux de la situation, sans respecter d’échelle.
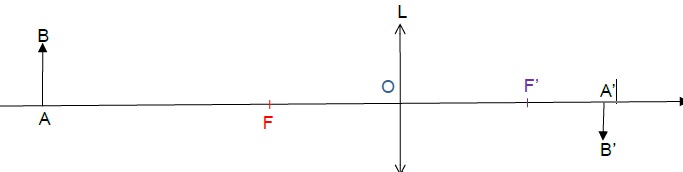
2. Pour le schéma
ci-dessus, qualifier l’image représentée avec deux des termes suivants
: image réelle, image virtuelle, image droite, image renversée.
L'image observée dans la station spatialle est réelle, plus petite que l'objet et renversée par rapport à l'objet.
3. Sans calcul, monter que le schéma ci-dessus modélise correctement la situation photographiée à bord de la station spatiale.
A'B', image de l'objet AB, est réelle et renversée.
Choix d’une lentille mince pour modéliser la bulle d’eau
Pour
reproduire la situation de la station spatiale, un groupe d’élèves
décide d’utiliser une lentille mince convergente de grand diamètre afin
de remplacer la bulle d’eau de la station
spatiale. On dispose au laboratoire d’une telle lentille (L) mais sa distance focale f ’ est inconnue.
Pour déterminer la valeur de la distance focale de cette lentille, les
élèves effectuent une série de mesures : pour différentes positions de
la lentille par rapport à l’objet, ils déplacent l’écran
pour former une image nette sur celui-ci, puis ils mesurent les valeurs algébriques OAet OA’.
Les élèves placent alors, après calculs, les points de mesure sur un
graphe et tracent en effectuant une régression linéaire la courbe de
tendance (en pointillés) dont l’équation y = f(x)
s’affiche ci-après.
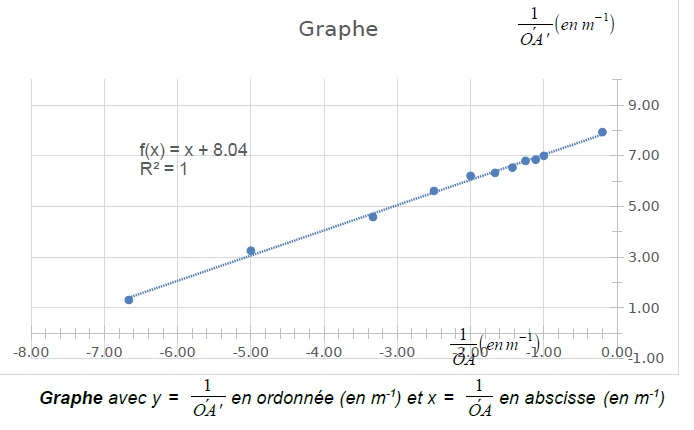
4. Les résultats expérimentaux obtenus sont-ils en accord avec la relation de conjugaison d’une lentille mince ? Justifier.
5. Déterminer la valeur de la distance focale f’ de la lentille (L).
1 / f ' = y -x ; y = 1 / f ' + x.
Le graphe y = f(x) est une droite. l'ordonnée à l'origine 8,00 est égale à 1 / f '.
f ' = 1 / 8,0 =0,125 m.
6. Conclure sur le fait que cette lentille puisse être utilisée ou non pour remplacer la bulle d’eau étudiée à la question 1.
Cette lentille convient , sa distance focale 12,5 cm est du même ordre de grandeur que celle de la bulle d'eau ( 5 cm)..
7. Justifier, en
choisissant deux propositions parmi celles ci-dessous, que le point de
mesure n° 11 (mesure algébrique OA = -5 m; mesure algébrique OA' =
0,126 m) permet d’estimer sans calcul la valeur de la distance focale
de la lentille mince (L). Préciser cette valeur.
Objet à l'infini par rapport à la lentille ; image dans le plan focal image de la lentille. ( f ' = 0,126 m).
Reproduction de la situation au laboratoire.
Le groupe d’élèves a ainsi reproduit au laboratoire la situation de la
station spatiale en remplaçant la bulle d’eau par une lentille mince
convergente (L) de grand diamètre (10,0 cm) et
de distance focale f’ dont la valeur sera assimilée à celle de la question 7 soit f ’ = 0,126 m.
L’astronaute est remplacé par un personnage en bois de hauteur 44,0 cm
dont le visage mesure 8,5 cm de haut. Un premier essai figure sur la
photographie 2.
Lors de la prise de vue, la distance entre la lentille (L) et le personnage est de 33,0 cm.

8. À l’aide des
informations sur les conditions dans lesquelles la photographie 2 a été
réalisée, déterminer par le calcul la valeur de la position et la
taille de l’image du personnage à
travers la lentille.
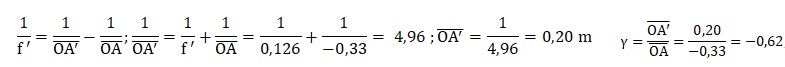
Taille de l'image renversée : 44 x 0,62 ~27 cm.
|
|
|