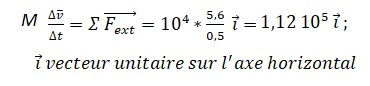Physique
chimie, exp�dition Gombessa 5 : plan�te m�diterran�e, les hydrogels
Haraguchi,
Etude d'une montagne russe.
E3C : enseignement de sp�cialit� premi�re g�n�rale.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicit�s adapt�es � vos centres
d’int�r�ts.
|
Exp�dition
Gombessa : plan�te m�diterran�e.
Partie 1 : comprendre les
particularit�s de la plong�e de Laurent Ballesta.
Le dispositif Gombessa 5.
Chaque jour, une tourelle descend les plongeurs depuis la station
flottante jusqu’� une profondeur de 120 m�tres. Ils remontent � la
surface pour manger et se reposer, mais toujours enferm�s dans un
module de vie et soumis � une pression 13 fois sup�rieure �
celle de l’atmosph�re. C’est une plong�e � saturation. Les sorties
sous-marines durent de 6 � 8 h.
Un
plongeur d�marre sa plong�e depuis la surface et est initialement
soumis � la pression atmosph�rique. Le profil donne la dur�e de chaque
�tape de la plong�e. Profil recommand� pour une plong�e � 120 m de
profondeur sans dispositif Gombessa 5
En plong�e les gaz sont comprim�s � la descente et d�tendus � la
remont�e. Il importe donc que ceux-ci puissent circuler librement dans
l’organisme du plongeur. Si ce n’est pas le cas, les parois des cavit�s
peuvent �tre l�s�es. Ces accidents sont appel�s � barotraumatismes �.
Le plus grave est la � surpression pulmonaire � qui touche le plus
souvent les plongeurs d�butants.
La remont�e doit se faire en respectant scrupuleusement des paliers de
d�compression pour �viter toute embolie gazeuse (pr�sence de bulles
dans la circulation sanguine). Source : d’apr�s
http://culturesciences.chimie.ens.fr.
1.1. D�terminer la
dur�e d’observation du fond marin � une profondeur h = 120 m pour un
plongeur qui n’utilise pas le dispositif Gombessa 5.
Environ 13 minutes.
1.2. D�terminer la
valeur de la pression en pascal (Pa) � laquelle est soumise un plongeur
� une profondeur h = 120 m. Comparer avec l’indication donn�e dans le
document d�crivant le dispositif Gombessa 5.
Masse volumique de l’eau de mer � 18 �C rmer = 1028 kg m–3
.
Pfond - Patmosph�rique = rmer g h =1028
x9,81 x120 =1,21 106 Pa.
Pfond = 1,21
106 +1,02 105 =13,1 106 Pa = 13,1 bar.
Valeur en accord avec " pression
13 fois sup�rieure � celle de l’atmosph�re".
1.3.
Justifier l’int�r�t du dispositif Gombessa 5 et des plong�es �
saturation r�alis�es par l’�quipe de Laurent Ballesta pour faire ses
observations � 120 m de profondeur. Au moins deux �l�ments de r�ponses
sont attendus.
Les sorties sous-marines peuvent durer de
6 � 8 h au lieu de 13 minutes.
Pas de soucis d'accidents lors de la remont�e.
Partie 2 : mais quelle est
donc cette dr�le de voix ?
� Dans notre caisson nous respirons un air pauvre en oxyg�ne.
Normalement la proportion d'oxyg�ne dans l'atmosph�re est de 21 % et de
79 % d'azote. L� c’est essentiellement de l'h�lium (90 %) et seulement
3 � 4 % d'oxyg�ne […]. Mais il transforme les voix en voix de canard et
pour se comprendre nous portons un casque micro qui corrige cette
d�formation �. Laurent Ballesta D’apr�s http://inpp.org.
La parole humaine : un ph�nom�ne tr�s complexe.
La hauteur du son �mis d�pend de plusieurs facteurs comme les
dimensions du larynx, la tension des cordes vocales et la vitesse de
propagation du son dans l’air. Le gaz qui sert � la production de la
voix est le gaz expir� mais quelle que soit la c�l�rit� du son produit,
la longueur
d’onde l du son
�mis est toujours la m�me. D’apr�s
http://phymain.unisciel.fr/de-lhelium-pour-parlercomme- mickey/
On souhaite en laboratoire reproduire la modification de la voix de
Laurent Ballesta. On enregistre � l’aide d’une interface.
Donn�es � la temp�rature de 20 �C :
c�l�rit� du son dans l’air : vair = 3,43 � 10 2
m s–1 ;
c�l�rit� du son dans l’h�lium : vh�lium = 1,02 � 10 3
m s–1.
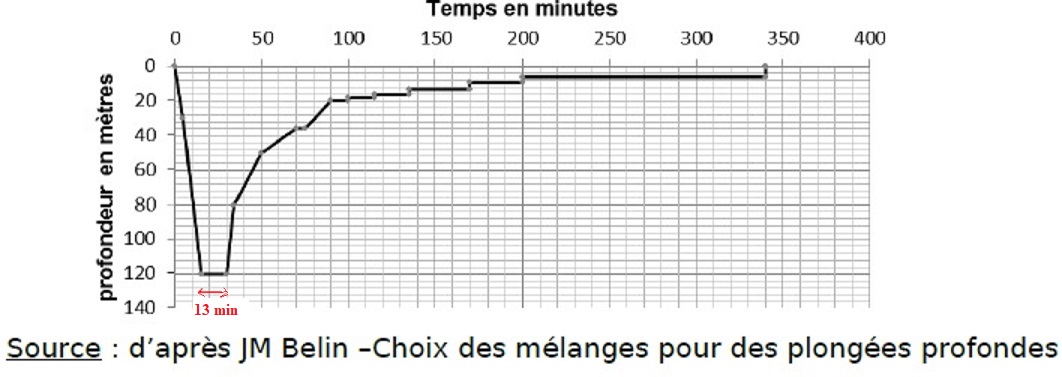
2.1. D�terminer le
plus pr�cis�ment possible la valeur de la p�riode T du signal
enregistr�. Une r�daction d�taill�e est attendue.
T = 13,6 / 6 ~2,27 ms = 2,27 10-3 s.
2.2. En d�duire la
valeur de la fr�quence f du son �mis.
f = 1 / T = 1 / (2,27 10-3) ~4,41 102 Hz.
2.3. On souhaite
d�terminer la longueur d’onde l
du son �mis. On dispose de deux micros plac�s c�te � c�te. Les signaux
capt�s par les deux micros sont en phase. On d�place un des deux micros
jusqu’� ce que les deux signaux reviennent pour la premi�re fois en
phase. La distance qui s�pare les micros est alors d = 76,9 cm.
2.3.1. Donner la
d�finition de la longueur d’onde d’un signal sinuso�dal.
La longueur d'onde est la distance parcourue par le front d'onde durant
une p�riode.
2.3.2. D�terminer
la valeur de la longueur d’onde du son �mis. Expliquer comment
am�liorer la pr�cision de la mesure.
l = d
= 0,769 m.
D�placer l'un des micros jusqu'� ce l'on observe la 5�me
fois ( par exemple ) le retour des signaux en phase.
La distance s�parant les micros sera �gale � cinq longueurs d'onde.
Diviser cette distance par 5.
2.4. � partir des
mesures effectu�es d�terminer la valeur c�l�rit� du son dans l’air.
Commenter.
v = l / T = l f = 0,769 x 4,41 102
=339 m /s.
Ecart relatif : ( 343 -339) / 343 ~0,011 ( 1 %).
Accords des deux valeurs � 1,1 % pr�s.
2.5. On souhaite
reproduire l’effet � voix de canard � observ� par les plongeurs.
D�terminer la valeur de la fr�quence avec laquelle on doit r�gler le
g�n�rateur pour imiter la modification d’un son �mis cette fois dans
l’h�lium, sachant que la longueur d’onde du son �mis est conserv�e
mais que la c�l�rit� du son dans l’h�lium est diff�rente de celle dans
l’air. Commenter.
fr�quence = vh�lium / l =1,02 103 /
0,769 ~1,33 103 Hz.
Dans l'air, un son de cette fr�quence serait plus aigu.
Partie 3 : retrouver la
tourelle � la fin de la plong�e : se localiser sous l’eau.
Le syst�me de positionnement mondial (GPS) pour se localiser sur Terre
utilise les ondes �lectromagn�tiques issues d’au moins quatre
satellites. Mais sous l’eau, il est impossible de les utiliser car
elles ne p�n�trent quasiment pas l’eau. La technologie qui est
actuellement mise au point consiste donc � utiliser des ondes
acoustiques.
Pr�sentation du syst�me GPS sous-marin.
Le bateau �met un signal ultrasonore qui est capt� et renvoy� par la
balise que porte � son poignet le plongeur. L’ordinateur de bord du
bateau enregistre les deux signaux et d�termine la distance entre le
plongeur et le bateau.
C�l�rit� des ondes ultrasonores dans l’eau en fonction de la
temp�rature pour une salinit� (teneur en sel) de 38 ‰
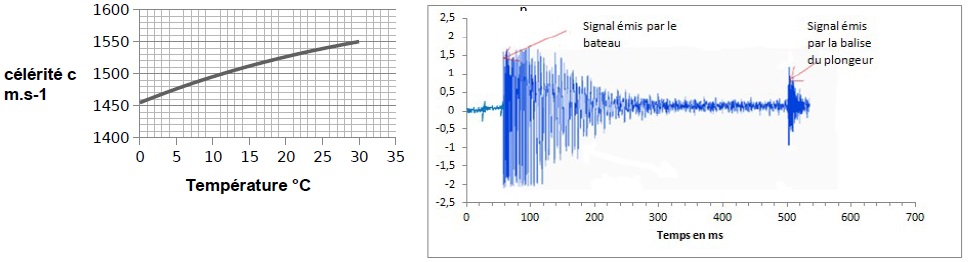
Amplitude des signaux enregistr�s par l’ordinateur situ� sur le bateau
au cours du temps
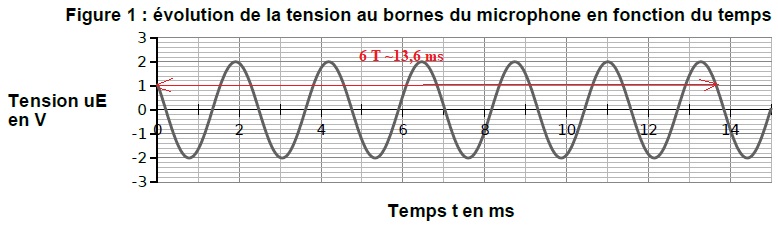
� partir des documents ci-dessus, d�terminer � quelle distance du
bateau est situ� le plongeur. La temp�rature moyenne de l’eau est de 18
�C.
Expliquer si cette seule mesure est suffisante pour d�terminer la
position exacte du plongeur.
C�l�rit� des ondes sonores dans l'eau de mer � 18 �C : 1520 m / s.
Dur�e s�parant les deux �missions : 540 ms = 0,54 s.
Distance bateau - plongeur : 1520 x 0,54 = 8,2 102 m.
Le plongeur se trouve � 820 m du bateau, mais on ne sait pas dans
quelle direction. Pour localiser le plongeur, il faudrait au moins un
autre dispositif �metteur-r�cepteur situ� sur une balise, situ�e � une
position pr�cise et fixe par rapport au bateau.
|
|
Les
hydrogels Haraguchi.
L’objectif de cet exercice est de s’int�resser aux esp�ces chimiques et
solutions mises en jeu dans le protocole exp�rimental de synth�se
d'hydrogels Haraguchi r�dig� ci-apr�s :
- dans un ballon de 50 mL, introduire un volume de 5 mL d’eau distill�e
;
- introduire un volume de 1,0 mL d'une solution aqueuse de persulfate
de potassium de concentration molaire apport�e en persulfate de
potassium C = 1,85 � 10 -1 mol.L-1 ;
- introduire 24 μL de TEMED (N,N,N’,N’- t�tram�thyl�thyl�nediamine), et
3,0 mL d’une solution aqueuse de DMAA (N,N - dim�thylacrylamide) ;
- agiter la solution pendant une dur�e de 15 minutes sous atmosph�re de
diazote ;
- ajouter une solution de laponite (petites billes d'argile) et garder
2 minutes sous agitation ;
- verser le m�lange dans un moule et laisser s�cher au moins douze
heures.
D’apr�s ESPCI :
https://blog.espci.fr/pse1/files/2018/06/materiel-et-methodes-Haraguchi.pdf.
1. Donner les
pr�cautions � prendre pour r�aliser la synth�se d'hydrogels Haraguchi
au laboratoire.
Certains r�actifs sont corrosifs, canc�rig�ne, dangereux pour
l'environnement. Port de blouse, gants et lunettes ; travail sous hotte
aspirante ; ne rien jeter � l'�vier.
2. La configuration
�lectronique du potassium K est 1s2 2s2 2p6
3s2 3p6 4s1. �crire la formule de
l’ion potassium. Justifier. En d�duire la charge de l’ion persulfate
associ� � l’ion potassium dans persulfate de potassium K2S2O8.
Afin d'acqu�rire la structure �lectronique du gaz noble le plus proche
( couche �lectronique externe compl�te ), l'atome de potassium c�de un
�lectron ; donc K+.
Le persulfate de potassium
�tant �lectriquement neutre : l'ion persulfate s'�crit S2O8
2-.
3. Citer l'interaction � l'origine
de la coh�sion du persulfate de potassium solide.
Interaction ionique.
4. �crire
l'�quation de la r�action de dissolution du persulfate de potassium
solide dans l'eau.
K2S2O8 (s) --> 2 K+ aq +
S2O8
2-aq.
� partir de persulfate de
potassium solide, on souhaite pr�parer un volume V = 100 mL de solution
aqueuse de persulfate de potassium de concentration molaire apport�e en
persulfate de potassium C = 1,85 � 10 -1 mol.L-1.
5. R�diger le
protocole exp�rimental permettant de r�aliser cette solution en
pr�cisant la verrerie, les volumes et masses pr�lev�s.
M(K2S2O8) =270 g / mol.
n(K2S2O8)
=0,100 x 0,185 = 0,0185 mol.
Masse � peser : 0,0185 x 270 =4,995 ~ 5,0g.
Placer une coupelle sur une balance de pr�cision et appuyer sur tare ;
peser 5,0 g de solide.
Verser dans une fiole jaug�e contenant 1 / 3 d'eau distill�e, surmont�e
d'un entonnoir ; rincer coupelle et entonnoir.
Agiter jusqu'� dissolution compl�te. Compl�ter jusqu'au trait de jauge
avec de l'eau distill�e.
Boucher et agiter pour rendre homog�ne.
6. �tablir la repr�sentation de
Lewis de la mol�cule de DMAA et pr�ciser la g�om�trie de cette mol�cule
autour de l'atome d'azote. Justifier.
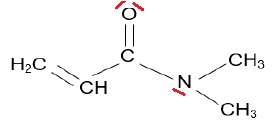
Pyramide � base triangulaire, le sommet �tant occup� par le doublet non
liant.
7. La mol�cule de
DMAA est une mol�cule polaire. Parmi les liaisons chimiques de cette
mol�cule de DMAA, pr�ciser celles qui sont polaris�es.
L'atome d'oxyg�ne est plus �lectron�gatif que l'atome de carbone : la
liaison C=O est polaris�e.
L'atome d'azote est plus �lectron�gatif que l'atome de carbone : les
liaisons C-N sont polaris�es.
8. En d�taillant
le raisonnement, expliquer pourquoi la mol�cule d’eau est polaire. Un
sch�ma est attendu. Justifier alors l'emploi de l'eau comme solvant
dans cette synth�se.
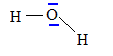
L'atome d'oxyg�ne plus
�lectron�gatif que l'atome d'hydrog�ne, porte une charge partielle
n�gative, ajout�e aux deux doublets non liants : la mol�cule d'eau est
polaire. La mol�cule
de DMAA est polaire ; elle est soluble dans un solvant polaire comme
l'eau.
Ci-dessous sont repr�sent�es de mani�re simplifi�e des macromol�cules
d’hydrogels synth�tis�es avec notamment les substituants aux cha�nes de
polym�res provenant du DMAA :
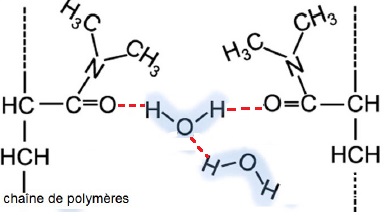
9. Nommer la (les)
interaction(s) qui existe(nt) entre l’hydrogel et l’eau et expliquer
succinctement pourquoi l’on parle d’hydrogels � superabsorbants �.
Des liaisons hydrog�ne ( en pointill�s sur le sch�ma ) s'�tablissent
entre les mol�cules d'eau et la mol�cule de DMAA : d'o� le caract�re "
super absorbant" de ces mol�cules.
Des histogrammes repr�sentant le pourcentage d'�longation � la rupture*
en fonction de la quantit� de mati�re de laponite sont repr�sent�s
ci-dessous pour des �chantillons t�moins (�chantillons neufs) et des
�chantillons cicatris�s, c’est-�-dire coup�s en deux puis appos�s
c�te � c�te pour permettre l’autocicatrisation du gel.
* L’�longation � la rupture est l’�longation maximale support�e par
l’�chantillon d’hydrogels Haraguchi avant qu’il ne se fracture.
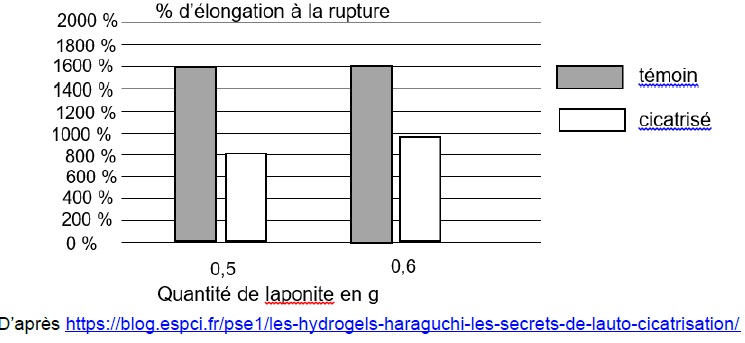
10. Commenter ces
histogrammes.
Apr�s cicatrisation, l'�longation � la rupture est divis�e par
deux lorsque la quantit� de laponite est de 0,5 g. Par contre,
elle n'est divis�e que par 1,6 lorsque la quantit� de laponite est de
0,6 g. Apr�s cicatrisation,
l'�longation � la rupture cro�t avec la masse de laponite.
|
Etude
d'une montagne russe.
Dans
cette attraction le train est lanc�, c’est-�-dire qu’un moteur lin�aire
lui procure l’�nergie cin�tique n�cessaire pour parcourir l’ensemble de
l’attraction
avant la premi�re bosse. Source : d’apr�s https://www.europapark.de/fr
L’objectif de cet exercice est de v�rifier la coh�rence de certaines
informations fournies par le constructeur de l’attraction et notamment
d’apporter un regard critique sur la pr�cision des
donn�es fournies.
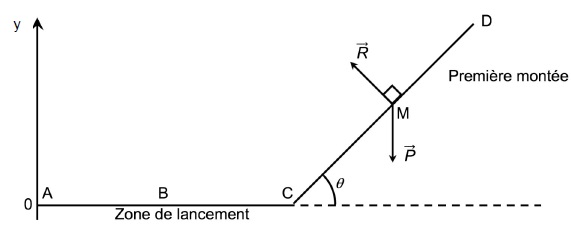
Le train est initialement immobilis� au point A avec la vitesse initiale v0 = 0 m.s – 1. Gr�ce � un moteur lin�aire �lectrique il est acc�l�r�, sur une piste horizontale, par une force constante
entre les points A et B pendant une dur�e Dt = 2,5 s pour atteindre sa vitesse maximale vmax = 100 km / h au point B. � partir du point C, il parcourt la premi�re mont�e pour atteindre son sommet au
point D � une hauteur h = 38 m au-dessus de la piste de lancement. On
consid�re, en premi�re approximation, que les frottements sont
n�gligeables.
1 . �tude de la chaine �nerg�tique.
1.1. La cha�ne �nerg�tique sch�matise la conversion d’�nergie lors du lancement du train.
Le moteur �lectrique convertit l'�nergie �lectrique en �nergie
m�canique ; une partie de l'�nergie re�ue est convertie en �nergie
thermique.
1.2. Montrer que l’�nergie cin�tique du train Etrain � la fin de la phase de lancement vaut 3,9 MJ.
Masse du train = 10 t = 1,0 104 kg.
Etrain = �mv2max avec vmax = 100 / 3,6 =27,77 m /s.
Etrain = 0,5 x1,0 104 x 27,772 ~3,9 106 J = 3,9 MJ.
1.3. Le rendement du moteur lin�aire �tant donn� par la relation Etrain / E�lectrique o� E�lectrique est l’�nergie �lectrique fournie au moteur lin�aire, d�terminer la valeur du rendement.
Commenter la valeur obtenue en apportant un regard critique sur les donn�es fournies par le constructeur.
Puissance du moteur lin�aire : P = 1,5 MW.
Eelectrique = P Dt =1,5 x 2,5 = 3,75 MJ.
Rendement : 3,9 / 3,75 ~1,04.
Un rendement ne peut pas �tre sup�rieur � 1 : les informations fournies par le constructeur sont fausses.
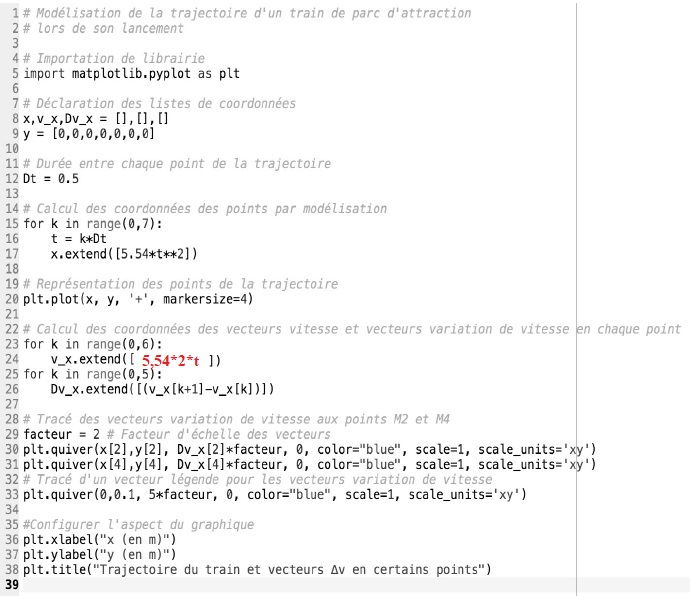
2 . Simulation de la propulsion du train.
Afin d’illustrer la phase de lancement, le programme suivant �crit en
langage Python permet de simuler la trajectoire du train ainsi que de
tracer les vecteurs variation de vitesse Δv en
quelques points de cette trajectoire sur une dur�e Δt. Le mod�le
utilis� formule l’hypoth�se d’un mouvement � acc�l�ration constante.
2.1. Compl�ter la
ligne 24 du programme de simulation en modifiant la partie entre les
crochets […] afin de calculer les coordonn�es vx[k] des vecteurs vitesses aux diff�rents points de la
trajectoire.
Le vecteur vitesse est la d�riv�e du vecteur acc�l�ration par rapport au temps : vx(t) = 5,54 x 2 x t et vy = 0 (trajectoire horizontale).
2.2. D�terminer graphiquement les valeurs Dv2 et Dv4 des normes des vecteurs Δv aux points M2 et M4.
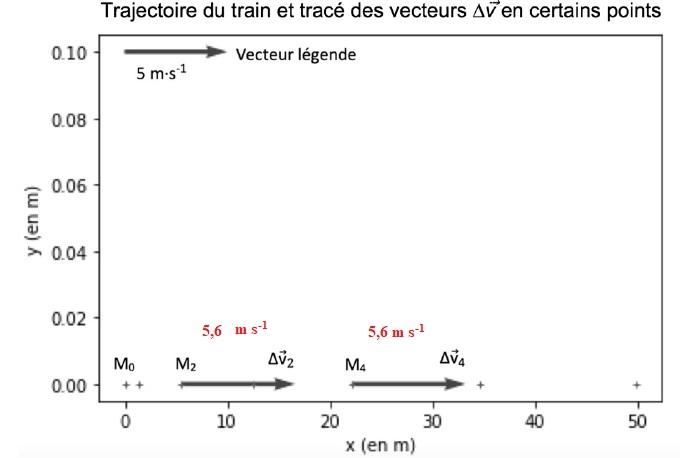
2.3. Expliquer comment semble �voluer le vecteur Δv au cours de la phase de lancement du train.
Le vecteur Δv est constant au cours de la phase de lancement.
2.4.
Donner la relation approch�e entre le vecteur variation de vitesse Δv
du train et la somme des forces ext�rieures qui s’appliquent sur
celui-ci.
2.5. En d�duire les caract�ristiques du vecteur ΣFext .
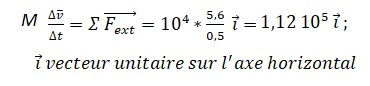
3 . �tude du train lors de la premi�re ascension.
On consid�re la premi�re mont�e CD comme rectiligne et faisant un angle q = 45� avec l’horizontale.
Le poids est une force conservative.
3.1. Exprimer le travail du poids sur le trajet CD en fonction de et de puis montrer que WCD (P)= m�g�(yC – yD).
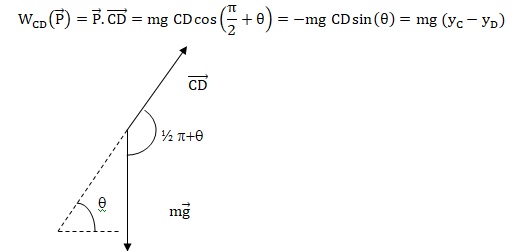
3.2. Donner la valeur du travail de la force de r�action des rails lors de la premi�re mont�e. Justifier.
La force de r�action des rails, perpendiculaire au plan, ne travaille pas.
3.3. �tablir l’expression de l’altitude maximale hmax que pourrait atteindre le train en l’absence de frottements puis calculer sa valeur. Commenter.
Th�or�me de l'�nergie cin�tique entre C et D :
La vitesse est nulle au point le plus haut : 0-�mv2max = mg(yC-yD)= -mghmax.
hmax = v2max / 2g) =27,772 /(2 x9,81) ~39 m.
En accord avec les donn�es du constructeur ( 38 m).
|
|
|
