Physique
chimie, étude d'une structure en béton, de la pose à l'analyse ; le ski
de vitesse.
E3C : enseignement de spécialité première générale.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
.
|
|
Etude
d'une structure en béton, de la pose à l'analyse.
1. Pression exercée par le
béton sur les fondations.
Le béton frais avant le début de son durcissement possède des
propriétés communes avec les liquides. Le béton frais exerce une
pression sur le coffrage qui l’entoure et sur les fondations. Il est
donc important d’estimer cette pression pour s’assurer que la structure
est suffisamment résistante.
Le coffrage représenté ci-dessous permet de construire un pilier carré
en béton de côté L = 30,0 cm et de hauteur h = 4,50 m ouvert du côté A.
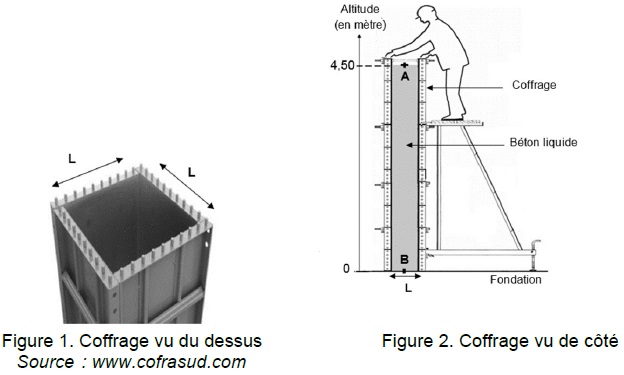
1.1. Indiquer la
valeur de la pression PA au point A en pascal (Pa).
La face supérieure est en contact avec l'atmosphère : PA =
1,00 105 Pa.
1.2. Montrer que la
valeur de la pression au point B est PB = 2,06×105 Pa.
Masse volumique du béton : r
= 2,40 103 kg m-3.
PB-PA = r
g h =2,40 103 x9,81 x 4,50 = 1,06 105 Pa ; PB
=1,00 105 +1,06 105 = 2,06 105 Pa.
1.3. Indiquer la
gamme de coffrage à utiliser pour construire ce pilier en béton.
Pression relative en B = 1,06 105
Pa = 106 kPa.
Le coffrage Cosfort métal résiste à une pression maximale de 120 kPa.
2. Étude de la qualité du
béton.
Une fois la structure en béton réalisée, il est possible de contrôler
sa qualité (résistance, défauts, position des armatures, etc.) grâce à
des techniques utilisant des ondes de différentes natures. La
gammagraphie est une méthode d’inspection des constructions en béton
qui est utilisée pour localiser les armatures en fer contenues dans le
béton.
L’émission de rayonnement gamma par le Cobalt 60 se fait en plusieurs
étapes :
- 1ère étape : en subissant une désintégration radioactive le Cobalt 60
se transforme en du Nickel 60 à l’état d’énergie E3 (2,5 MeV
);
- 2ème étape : la désexcitation de l’atome de Nickel de l’état
d’énergie E3 à l’état d’énergie E1 entraîne
l’émission d’un rayonnement ;
- 3ème étape : l’atome de Nickel se désexcite une seconde fois passant
du niveau d’énergie E1 ( 1,3 MeV ) au niveau fondamental.
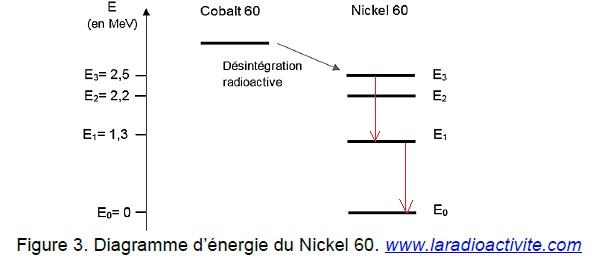
2.1. Reproduire sur
votre copie le diagramme d’énergie du Nickel 60 de la figure 3 et
présenter les transitions correspondant à la 2ème et la 3ème étape
évoquées dans le texte.
2.2. Montrer que
l’énergie d’un photon émis lors de la 2ème étape vaut E = 1,9×10-13
J.
2,5 -1,3 = 1,2 MeV = 1,2 106 eV; 1,2 106 x1,6 10-19
= 1,9×10-13
J.
2.3.
Calculer la fréquence de l’onde émise lors de la 2ème étape. Justifier
le nom donné à cette méthode d’inspection.
Fréquence = énergie ( J) / constante de Planck = 1,9 10-13 /
(6,63 10-34) =2,9 1020 Hz.
Cette fréquence appartient au domaine des rayons gamma.
|
|
Étude par
onde ultrasonore.
L’utilisation d’ultrasons est un outil très adapté pour l’évaluation
non destructive des bétons. Il est possible de détecter des
microfissures en étudiant la propagation d’onde ultrasonore dans le
béton. De plus, la vitesse de propagation des ondes ultrasonores est
reliée directement à la résistance du béton et donc à la qualité de
celui-ci.
La courbe ci-dessous représente une simulation de la tension
d’alimentation d’un émetteur à ultrason utilisé pour le contrôle des
bétons :

L’émetteur génère des ondes ultrasonores de même fréquence que celle de
la tension qui l’alimente.
2.4. Calculer, en
MHz, la valeur de la fréquence des ondes utilisées par cet appareil. On
explicitera la méthode utilisée.
f = 1 / T = 1 /(5,0 10-8) =2,0 107 Hz = 20 MHz.
Pour qu’un défaut dans la structure soit détectable, il faut qu’il ait
une taille au moins égale à la moitié de la longueur d’onde ultrasonore.
La vitesse des ondes ultrasonores peut aller jusqu’à 4 500 m∙s-1
dans le cas des bétons de grande qualité.
2.5. Une fissure
est à considérer comme anormale dès qu’elle dépasse 0,3 mm de largeur.
Est-il possible de détecter, dans un béton de grande qualité, une
fissure de 0,3 mm à l’aide de cet émetteur à ultrason ?
Longueur d'onde = célérité ( m /s) / fréquence ( Hz) =4500 / (2,0 107)
=2,25 10-4 m ~ 0,23 mm.
Demi-longueur d'onde : ~0,12 mm. La fissure est détectable.
Dans le cas d’un béton soumis au feu, l’élévation de température
provoque une modification physico-chimique du matériau. L’auscultation
aux ultrasons, fondée sur des mesures de temps de parcours d’onde
ultrasonore est une méthode particulièrement bien adaptée pour remonter
à
la résistance du béton et ainsi déterminer si une zone a été trop
endommagée par le feu. L’auscultation aux ultrasons consiste à envoyer
des ultrasons à l’aide d’un émetteur (E). On place ensuite tous les 20
cm des récepteurs (R1 à R4) et on mesure la durée
de trajet du signal.
D’après le laboratoire central des Ponts et Chaussées.
Résultats pour le bloc de béton soumis au feu :
récepteur
|
distance
émetteur- récepteur ( cm)
|
temps
de réception du signal( µs)
|
R1
|
20
|
62
|
R2
|
40
|
121
|
R3
|
60
|
195
|
R4
|
80
|
278
|
On considère qu’une zone
de béton de qualité médiocre ( vitesse des ultrasons comprise
entre 2000 et 3000 m/s) ou inférieure est éliminée par piquage pour
réparation ou reconstruction.
2.6. Déterminer si
le morceau de béton compris entre les récepteurs R2 et R3
ausculté doit subir des réparations.
Distance entre R2 et R3 : 20 cm = 0,20 m.
Durée de ce parcours :195-121 =74 µs = 7,4 10-5 s.
Célérité des ultrasons : 0,20 / (7,4 10-5) =2,7 103
m /s.
Cette zone de béton est de qualité médiocre et nécessite une
réparation.
|
Le ski de
vitesse.
Partie 1 : étude énergétique du mouvement du skieur dans l’hypothèse de frottement négligeable.
Le système étudié est le « skieur » constitué de l’athlète avec son
équipement de masse totale m et de centre de masse G en mouvement sur
la piste de ski d’un point D d’altitude zD à un
point A d’altitude zA.
Le départ s’effectue sans vitesse initiale. Le référentiel d’étude est
supposé galiléen. Dans cette partie les frottements subis par le
système sont négligés devant les autres actions mises en jeu.
1.1. Effectuer le
bilan des actions, modélisées par des forces, agissant sur le système.
Préciser le sens et la direction de chaque force.
Poids, verticale vers le bas ; action du plan, perpendiculaire au plan, vers le haut.
1.2. Calculer le travail WDA de chaque force entre le point de départ D et le point d’arrivée A.
L'action du plan, perpendiculaire à la vitesse ( donc au déplacement ) ne travaille pas.
Travail moteur du poids en descente : W = mg (zD-zA).
m = 102 kg ; zD =2720 m ; zA=2285 m.
W = 102 x9,8 x(2720 -2285)=4,348 105 ~4,3 105 J.
1.3. En utilisant le théorème de l’énergie cinétique, déduire la valeur de la vitesse à l’arrivée, notée vA, en m.s-1 puis en km.h-1.
½mv2A-0 = W ; vA = (2 W / m)½ =(2 x4,348 105/102)½ ~92 m /s.
92 x3,6 = 3,3 102 km / h.
1.4. Cette valeur
est-elle en accord avec celle de la vitesse atteinte ( 252 km /h )le
vendredi 3 avril 2015 par Simone Origone ? Quel aspect de la
modélisation effectuée doit être remis en
cause ?
La valeur trouvée n'est pas en accord avec la valeur réelle. Il faut tenir compte des frottements.
Partie 2 : mouvement d’un mobile autoporteur.
On se propose de mesurer l'intensité des actions de frottements qui
agissent sur un mobile en mouvement. Ces actions seront modélisées par
une force constante, d’intensité f , et de sens
opposé au vecteur vitesse.
Ce mobile, de centre de masse G, de masse m = 220 g, est abandonné sans vitesse sur un plan incliné d'un angle a0 par rapport à l'horizontale. Au cours de son mouvement, le mobile suit
la ligne de plus grande pente de direction Ax, la position de G est
repérée en fonction du temps par sa coordonnée x dans le repère.
Une vidéo du mouvement est réalisée. Un logiciel de pointage permet de
relever les valeurs de la position x et de l'altitude z sur l’axe
vertical Oz du centre d'inertie G à des intervalles de
temps réguliers et de déterminer à chaque pointage la valeur de la vitesse du mobile le long de l'axe Ax.
Un programme python permet de représenter l’évolution de l’énergie cinétique Ec du système au cours du temps. On obtient la courbe ci-dessous.
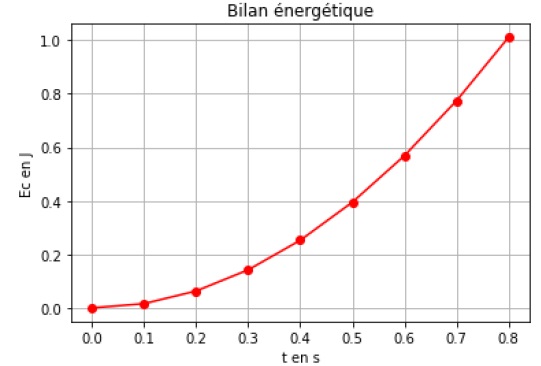
2.1. Modifier le
script du programme en ajoutant une ligne de code (ligne 14) qui
permettra de déterminer la valeur de l’énergie potentielle E pp du système. Quelle donnée faut-il ajouter au script ? Compléter alors la ligne 5.

Le script est ensuite encore modifié pour faire apparaître l’énergie
cinétique, l’énergie potentielle et l’énergie mécanique. On obtient les
courbes ci-dessous. L’énergie potentielle de pesanteur est
choisie nulle en O.
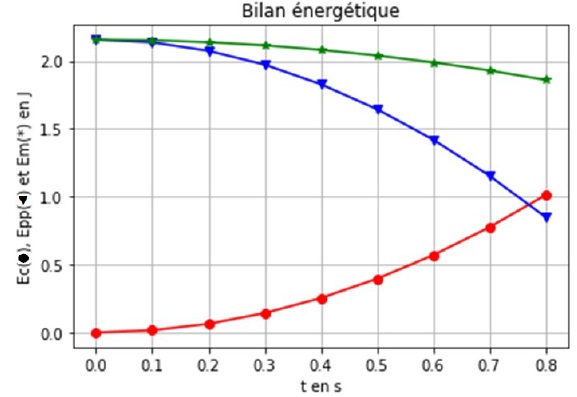
2.2. Comment expliquer l’évolution de l’énergie mécanique au cours du temps ?
L'énergie mécanique diminue du travail des frottements.
2.3. Compléter le schéma en représentant les forces modélisant les actions sur le système.
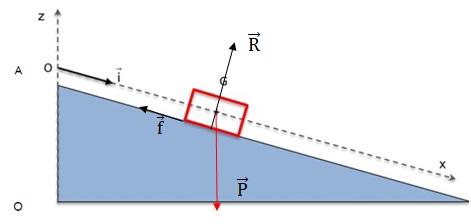
2.4. En tenant compte des valeurs relevées dans le tableau, calculer les valeurs de l’énergie mécanique Em0 et Em8 respectivement aux instants t0 = 0,000 s et t8 = 0,800 s.
numéro
|
t(s)
|
x(m)
|
v (m/s)
|
z(m)
|
Ec(J)
|
Epp(J)
|
Em(J)
|
0
|
0
|
0
|
0
|
1,000
|
0
|
0,22 x9,8 x1
~2,2
|
2,2
|
8
|
0,800
|
1,212
|
3,0312
|
0,394
|
0,5 x0,22x3,03122
~1,0
|
0,22 x9,8 x0,394
~0,86 |
1,0 +0,86 ~1,9
|
2.5. À l’aide d’une bilan énergétique, montrer que dans le cadre de ce modèle : f = (Em0−Em8) / (x8−x0).
L'énergie mécanique diminue du travail des forces de frottement.
Travail des forces de frottement : -f (x8-x0).
Em8−Em0 =-f (x8-x0).
2.6. Déterminer la valeur de l’intensité de la force modélisant les frottements s’exerçant sur le mobile. Commenter.
f = (2,2-1,9) / (1,212-0) ~0,36 N.
Cette force n'est pas négligeable devant le poids ( 0,22 x9,8 ~2,2 N ).
Partie 3 : retour qualitatif sur l’étude énergétique du mouvement du skieur.
3. Quelles sont les
causes des actions de frottement exercées sur le skieur ? Discuter de
l’influence de la valeur de la vitesse et de la pertinence d’une
modélisation de ceux-ci par
une force d’intensité constante.
Frottements des skis sur la piste.
Frottement sur les couches d'air. Ceux -ci dépendent de la vitesse voir du carré de la vitesse pour des vitesses élevées.
Le modèle d'une force de frottement constante n'est pas valide pour des vitesses importantes.
|
|
|






