Physique
chimie, Solar Impulse 2, l'avion solaire,
un modèle pour la balle de tennis pendant le service,
E3C : enseignement de spécialité première générale.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
.
|
|
Solar
Impulse2, l'avion solaire..
L'avion solaire Solar Impulse 2 restera dans l’histoire de
l’aéronautique comme le premier avion à avoir bouclé avec succès un
tour du monde (43 041 km parcourus en 17 étapes) sans une goutte de
carburant et avec le Soleil comme unique source d’énergie. Au cours de
ce tour du monde, cet avion piloté alternativement par les pilotes
suisses Bertrand Picard et André Borschberg aura notamment :
- effectué sa première traversée de l’Atlantique entre New York et
Séville ;
- établi le plus long vol de l’histoire sans escale et sans pilote
automatique (117 heures 52 minutes entre Nagoya et Hawaï).
Ce tour du monde aura été rendu possible grâce à des choix
technologiques innovants et un profil de vol raisonné.
Partie 1 : le solaire
photovoltaïque.
Solar Impulse 2 est presque entièrement recouvert de panneaux solaires
photovoltaïques. Les matériaux semi-conducteurs utilisés pour
constituer les cellules photovoltaïques sont le résultat de nombreuses
recherches.
On s’intéresse dans cette partie à la production d’électricité par
l’effet photovoltaïque.
L’effet photovoltaïque.
Dans un semi-conducteur exposé à la lumière, un photon d’énergie
suffisante extrait un électron qui participe à la conduction de
l’électricité. La valeur minimale d’énergie apportée par le photon doit
être Emin = 1,12 eV.
1.1 Montrer qu’un
photon d’énergie 1,12 eV est associé à un rayonnement de longueur
d’onde λ voisine de 1 μm.
Emin = 1,12 *1,6 10-19 =1,792 10-19
J.
l =
hc / Emini =6,62 10-34 x 3,00 108
/(1,792 10-19) =1,1 10-6 m = 1,1 µm.
1.2 À quel domaine
des ondes électromagnétiques ces ondes appartiennent-elles ?
Proche infrarouge.
1.3 Expliquer
pourquoi les matériaux semi-conducteurs présentent un intérêt dans le
fonctionnement des cellules photovoltaïques.
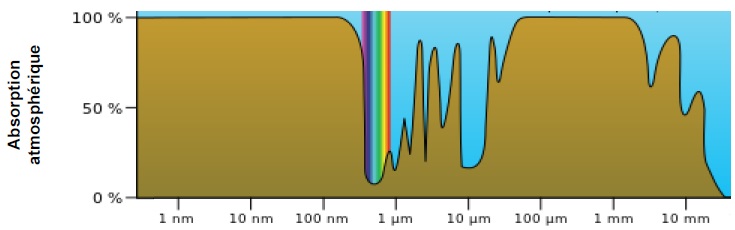
L'atmosphère absorbe très peu les photons de longueur d'onde 1 µm.
Partie 2 : les
performances des panneaux solaires de Solar Impulse 2.
On se propose d’étudier en laboratoire une cellule photovoltaïque «
classique » afin de comparer son rendement à l’une des 17 000 cellules
qui équipent l’avion Solar Impulse 2.
Étude d’une cellule photovoltaïque « classique » en laboratoire.
Matériel à disposition :
- une lampe halogène ;
- un solarimètre ;
- une cellule photovoltaïque de surface utile S = 26,1 x 10-4 m2
;
- une résistance variable ; - un ampèremètre ; - un voltmètre ; - des
fils de connexion.
Protocole expérimental :
- brancher en série la cellule photovoltaïque et la résistance variable
;
- éclairer la cellule photovoltaïque à l’aide de la lampe halogène
placée à 10 cm, et mesurer l’éclairement Elum au niveau de
la cellule photovoltaïque en utilisant le solarimètre (la distance
lampe/cellule sera maintenue fixe tout au long de l’étude) ;
- pour différentes valeurs de la résistance R, relever les valeurs de
la tension U aux bornes de la cellule et de l’intensité I du courant
dans le circuit à l’aide des appareils de mesure correctement connectés
;
- tracer à l’aide d’un tableur grapheur la caractéristique I = f(U) de
la cellule photovoltaïque.
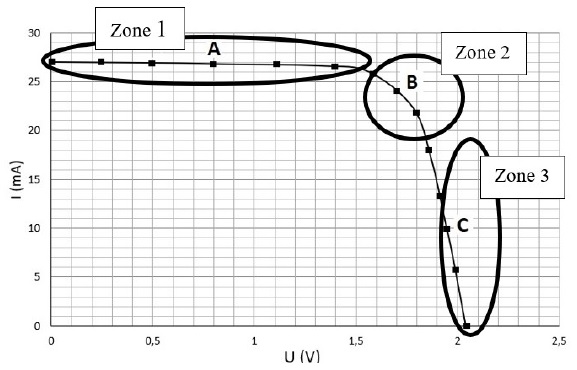
La caractéristique ci-dessous a été obtenue pour un éclairement Elum
= 300 W.m-2 (mesure effectuée avec le solarimètre).
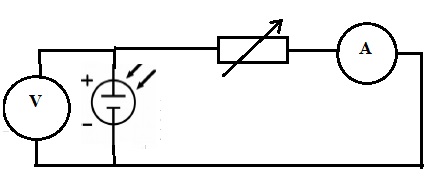
2.1.Schématiser le
montage électrique associé au protocole (le solarimètre ne sera pas
représenté sur votre schéma).
2.2. Dans quelle
zone (1, 2 ou 3) la puissance électrique délivrée par cette cellule
est-elle la plus grande ? Justifier la réponse en déterminant la
puissance électrique délivrée par la cellule aux points A, B et C.
Point A : U = 0,8 V et I = 27 mA ; P = UI = 0,8 x27 =21,6 mW.
Point B : U
= 1,7 V et I = 24 mA ; P = UI = 1,7 x24 =40,8 mW.
Point C : U
= 1,9 V et I = 10 mA ; P = UI = 1,9 x10 =19 mW.
La puissance délivrée est maximale dans la zone 2.
On
considère que la puissance électrique maximale délivrée par la cellule
photovoltaïque étudiée est Pelec_max = 0,041 W.
2.3. Montrer, en
justifiant par un calcul, que le rendement maximal de la cellule
photovoltaïque étudiée au laboratoire est ηmax = 5,2 %.
Rendement = puissance électrique délivrée / puissance solaire reçue
=0,041 / ( S Elum) =0,041 /( 26,1 10-4 x 300)
=0,052 ( 5,2 %).
2.4. Pourquoi le
rendement déterminé ne correspond-il pas à celui d'une cellule
photovoltaïque classique ( 15 % pour Elum = 1000 W m-2),
alors que la cellule étudiée peut être considérée comme une cellule
photovoltaïque « classique » ?
La cellule étudiée est soumise à un éclairement de 300 W m-2
et non pas 1000 W m-2.
2.5.Les cellules
photovoltaïques de Solar Impulse 2 ont un rendement de 23 %. Vous
paraissent-elles performantes ? Justifier la réponse.
Les cellules photovoltaïques de Solar Impule 2 sont construites avec du
silicium monocristallin. Leur rendement ( 23 %) est bien supérieur à
celui d'une cellule photovoltaïque classique. Seule une petite partie
du rayonnement solaire apporte des photons dont l'énergie est
supérieure à 1,12 eV. Les cellules solaires de cet avion sont très
performantes.
|
|
Partie 3
- Analyse du plan de vol de Solar Impulse.
Un avion motorisé est soumis à trois types d’actions mécaniques lors
d’un vol en palier stabilisé :
- la poussée du réacteur ou la traction T de l'hélice entraînée par le
moteur ;
- le poids P , effet de la gravité terrestre sur la masse de l'appareil
;
- la résultante des forces aérodynamiques décomposée en portance et en
traînée :
* la portance L créée par le déplacement dans l'air d'une aile
profilée, est opposée au poids.
* la traînée D, somme des résistances aérodynamiques, est opposée au
mouvement.
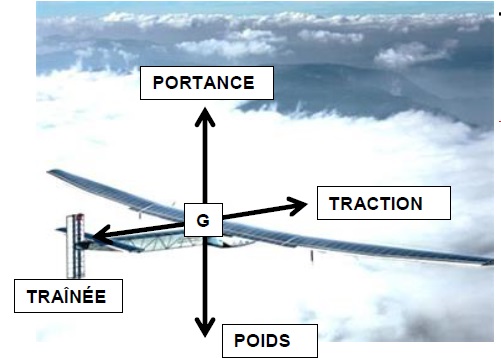
3.1 En vol
horizontal stabilisé, l’avion a un mouvement rectiligne et uniforme.
Justifier le fait que les intensités de la force de traction T et de la
force de trainée D sont égales.
Le mouvement étant rectiligne uniforme, la somme vectorielle des forces
appliquées à l'avion est nulle ( principe d'inertie ou première loi de
Newton ).
3.2 En effectuant
une analyse dimensionnelle, montrer que le coefficient de traînée Cx
intervenant dans l’expression littérale de l’intensité de la traînée
n’a pas d’unité.
T = ½ S Cx r V2.
T : N soit kg m s-2.
S m2 ; r
: kg m-3 ; V m s-1.
S r V2 s'exprime
en m2 kg m-3 m2 s-2 soit : kg m s-2.
3.3 Compte tenu de l’expression de
l’intensité de la trainée, montrer que la puissance PM
développée en vol stabilisé à vitesse constante par les moteurs peut
s’écrire sous la forme : PM =½ S Cx r V3.
Le mouvement étant rectiligne uniforme : Traction = trainée = ½ S Cx r V2.
La puissance PM est égale à l'intensité de le force fois la
norme de la vitesse.
3.4 En supposant que la vitesse de
l’avion est maintenue constante, comment varie cette puissance en
fonction de l’altitude ?
La masse volumique de l'air diminue avec l'altitude. PM est
proportionnelle à la masse volumique de l'air. PM diminue
avec l'altitude.
3.5 Calculer la
valeur de la puissance développée par les moteurs à 2000 mètres
d’altitude pour une vitesse de 45 km·h-1 et un coefficient Cx
= 0,012. On admettra que la surface S de l’avion soumise à la force de
traînée est de 197 m2.
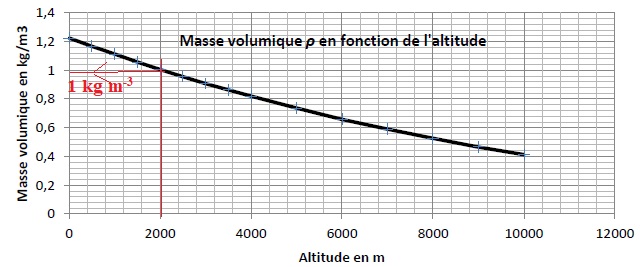
V = 45 / 3,6 = 12,5 m /s.
PM =0,5 x197 x0,012 x1 x 12,53=2,3
103 W
3.6 Quels arguments énergétiques
peut-on évoquer pour expliquer les différentes étapes du plan de vol de
l’avion sur 24 heures ?
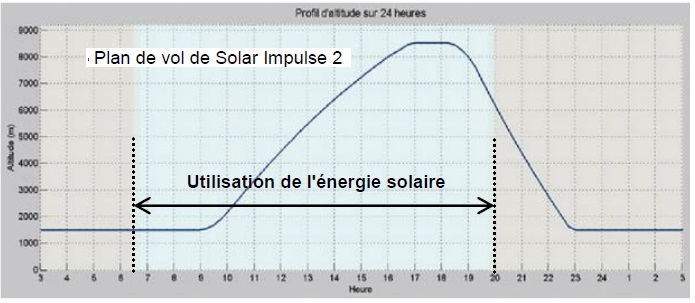
Entre 23 h et 6 h 30, les batteries sont utilisées afin que les moteurs
permettent de maintenir une altitude constante.
Entre 6 h 30 et 18 h 30, l'énergie solaire permet de recharger la
batteries et de faire fonctionner les moteurs. L'avion prende de
l'altitude et stocke de l'énergie potentielle de pesanteur et de
l'énergie chimique dans les batteries..
De 18 h 30 à 23 h, moteurs éteints, l'avion plane et restitue
l'énergie potentielle de pesanteu lors de sa descente.
|
Un modèle
pour la balle de tennis pendant le service.
1. Modélisation de la chute verticale de la balle.
Une balle, de masse m = 55 g, est lâchée sans vitesse initiale. On
filme ce mouvement de chute verticale et, à l'aide d'un logiciel
adapté, on relève les positions successives de la balle. Un programme
informatique permet de calculer les énergies cinétiques, potentielles
de pesanteur et mécaniques de la balle à partir des relevés.
L’origine du repère est prise au sol, et l’axe des altitudes est
dirigé vers le haut. On note A la position initiale de la balle lorsqu’elle
quitte la main de l’opérateur, et B son point d’impact, sur le sol.
1.1. On identifie trois forces qui peuvent s’exercer sur la balle lors
de son mouvement :
le poids P de la balle ;
la force de frottement f exercée par l’air sur la balle et qui dépend de la vitesse de la balle ;
la poussée d’Archimède F, indépendante de la vitesse de la balle,
qui est exercée par l’air sur la balle, dirigée vers le haut et de valeur F = r ⋅g ⋅V,
avec V le volume de la
balle et r la masse volumique de l’air.
Représenter sur votre copie un schéma de la balle modélisée par un
point en M, à un instant quelconque de son mouvement ainsi que les forces s’exerçant sur elle,
sans souci d’échelle.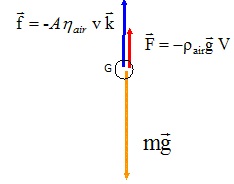
1.2. Comparer la valeur de la poussée d’Archimède au poids et en
déduire que la poussée d’Archimède est négligeable devant le poids.
Poids P = mg = 0,055 x9,8 ~0,54 N.
Le diamètre des balles de tennis est en moyenne de 6,5 cm. Masse volumique de l'air 1,0 kg m-3.
Volume de la balle V = 4 / 3 xp r3 =4 / 3 x3,14 x (3,25 10-2)3 =1,44 10-4 m3.
Poussée d'Archimède : 1,0 x1,44 10-4 x9,8 =1,4 10-3 N, valeur très inférieure à celle du poids.
1.3. Parmi les trois séries de points reproduites sur la figure
ci-après, identifier en justifiant la réponse :
la série de points qui correspond aux mesures de l’énergie cinétique ;
la série de points qui correspond aux mesures de l’énergie
potentielle de pesanteur ;
la série de points qui correspond aux mesures de l’énergie mécanique.
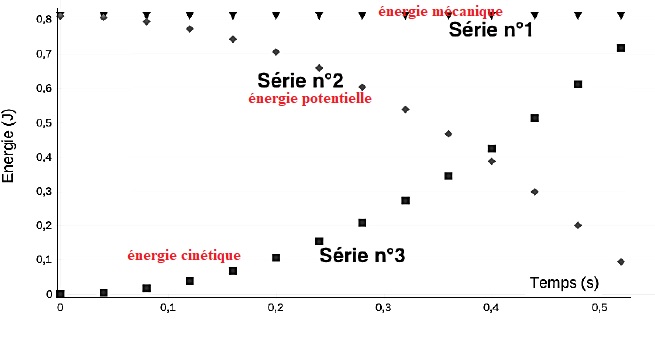
Série 3 : énergie cinétique ( la vitesse initiale, donc l'énergie cinétique initiale sont nulles.
Série 2: énergie potentielle de pesanteur, maximale à t = 0 puis décroît lors de la chute.
Série 1 : énergie mécanique, somme des énergies cinétique et potentielle.
1.4. À l’aide de ces courbes, justifier que l’on peut, dans cette étude, faire le choix de négliger les forces de frottement.
L'énergie mécanique étant constante, les forces de frottements sont négligeables.
1.5. À quelle force est due la variation d’énergie cinétique observée ? Donner la valeur de son travail sur le trajet AB.
Le travail du poids est moteur en descente. La variation de l'énergie
cinétique est égale au travail du poids ( seule force appliquée à la
balle ).
Wpoids = énergie potentielle initiale = 0,8 J.
2. Modélisation du service au tennis.
L'objectif de cette seconde partie est de vérifier si le modèle proposé
dans la première partie convient aussi pour le mouvement de la balle
lors du service, c’est-à-dire
une fois qu’elle a quitté la raquette, venant d’être frappée par le
joueur qui engage. Pour la suite de l’exercice, toutes les forces sont
négligées, sauf le poids.
La position initiale de la balle est notée C, lieu où le contact est
rompu avec la raquette. La vitesse de la balle en C, supposée
horizontale, est notée vC. Son altitude est notée zC. La balle atteint le sol au point D, à la vitesse de norme vD et à la même altitude que l’origine du repère choisi.
2.1. Reproduire la figure et la compléter en représentant l'allure de la trajectoire de la balle lors du service.
2.2. Montrer à
l’aide d’un théorème énergétique que, dans les conditions du modèle
proposé dans la première partie, la vitesse au point d'impact s'écrit :
vD=(vC 2 +2⋅ g ⋅zC)½.
Seul le poids travail ; ce travail est moteuur en descente et vaut W = mgzC.
Variation de l'énergie cinétique entre C et D : ½mvD2-½mvC2 .
Théorème de l'énergie cinétique : ½mvD2-½mvC2 =mgzC.
½vD2-½vC2 =gzC ; vD2-vC2 =2g zC ; vD=(vC 2 +2⋅ g ⋅zC)½.
2.3. Déterminer la valeur de vD pour zC = 2,20 m et vC = 200 km.h-1 pour ce modèle. Commenter.
200 / 3,6 = 55,5 m /s.
vD=(55,5 2 +2x9,8x2,20)½ ~55,9 m /s ( 201 km / h).
Cette valeur n'est pas réaliste, il faut prendre en compte les frotements de l'air sur la balle.
2.4. Avec les valeurs initiales précédentes, la valeur de la vitesse vDexp effectivement mesurée au point D est de l’ordre de 100 km.h-1. Proposer une hypothèse qui pourrait expliquer
l’écart entre les valeurs de la vitesse mesurée et de celle déterminée avec le modèle précédent.
Les forces de frottements doivent être prises en compte lorsque les vitesses sont grandes.
|
|
|








