Physique
chimie, la fosse de plongée Nemo 33 ; bouquet final, feu d'artifice.
E3C : enseignement de spécialité première générale.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
.
|
|
La fosse
de plongée Nemo 33.
Le
Nemo 33 est un centre de plongée à Uccle, en Belgique. Il possédait la
fosse de plongée la plus profonde du monde jusqu'en février 2014
atteignant une profondeur de près de 35 mètres. Une fosse de plongée
sert à pratiquer la plongée sous-marine ou la plongée en apnée.
1. Titrage des ions
hypochlorite ClO- présents dans l’eau d’une fosse de plongée.
Afin de maintenir la qualité sanitaire de l’eau d’une fosse de plongée
on y ajoute des ions hypochlorite ClO-, il s’agit d’un
oxydant puissant qui peut réagir avec des composés organiques et des
micro-organismes afin de les détruire. La réglementation impose une
concentration en « chlore actif » pour les piscines en France
correspondant à une concentration d’ions hypochlorite comprise entre
0,4 mg.L-1 et 1,4 mg.L-1.
Pour étudier les propriétés chimiques de l’eau d’une fosse de plongée
et déterminer sa concentration en ions hypochlorite, on effectue un
prélèvement. À l’aide d’une pipette jaugée, on prélève V1 =
20,0 mL d’eau d’une fosse de plongée que l’on place dans un bécher de
50 mL, on ajoute 1,0 mL d’une solution contenant des ions iodure en
excès et 1,0 mL une solution d’acide sulfurique puis on agite. Le
mélange obtenu, qui prend alors une teinte orange-brun, est appelé
solution S.
Les couples mis en jeu sont ClO-(aq)/Cl-(aq) et I2(aq)/I-(aq).
Le diiode a une coloration orange brun en solution aqueuse, c’est la
seule espèce colorée dans la solution S.
1.1. Justifier à
l’aide des observations expérimentales le caractère oxydant de l’eau de
la fosse de plongée.
1.2.
Écrire la demi-équation électronique associée au couple de
l’hypochlorite et justifier le rôle d’oxydant de cet ion.
1.3. Donner
l’équation de la réaction modélisant la transformation intervenant
entre les ions hypochlorite et les ions iodure.
Avant ajout d'ion iodure,
la solution est incolore ; après l'ajout, la solution contient du
diiode ( teinte orange-brun ).
L'ion iodure joue le rôle de réducteur, il céde des électrons : 2I-
aq ---> I2 aq + 2e- (1).
L'ion ClO- joue le rôle d'oxydant , il gagne des électrons :
ClO- aq +2H+aq + 2e- ---> Cl-
aq + H2O (2).
(1) +(2) donne : ClO- aq +2H+aq + 2e-
+2I- aq --->
Cl- aq + H2O + I2 aq + 2e-.
Simplifier : ClO- aq +2H+aq
+2I- aq --->
Cl- aq + H2O + I2 aq .
1.4. Établir le
tableau d’avancement de la réaction. Les ions iodure, I-(aq),
et oxoniums H+(aq), sont en excès, l’eau est le solvant.
|
avancement
(mol)
|
ClO-
aq |
+2H+aq |
+2I-
aq |
--->
Cl- aq |
+ I2 aq |
+ H2O |
initial
|
0
|
n
|
excès
|
excès
|
0
|
0
|
solvant
|
en
cours
|
x
|
n-x
|
x
|
x
|
fin
|
xf
= n
|
0
|
n
|
n
|
On considère dans la suite que tout le diiode dans la solution S
provient de la réaction entre les ions hypochlorite et iodure et que la
transformation est totale. Afin de déterminer l’avancement final xf
de cette réaction, on effectue un dosage par étalonnage du diiode dans
la solution S. On réalise une série de mesure d’absorbance de solutions
de concentrations connues en diode, les
résultats sont donnés dans le tableau ci-dessous :
concentration
en diiode ( µmol / L)
|
20
|
50
|
100
|
250
|
absorbance
A à 475 nm.
|
0,016
|
0,041
|
0,10
|
0,22
|
On effectue une mesure
d’absorbance pour la solution S, on obtient AS = 0,017.
1.5. Déterminer la
valeur de la concentration en diiode de la solution S. En déduire la
valeur de la quantité de diiode, formée lors de la réaction entre les
ions hypochlorite et iodure, et que la valeur de l’avancement final xf
est voisine de 4,6×10-7 mol.
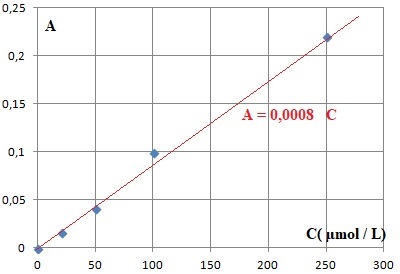
Concentration du diiode : 0,017 / 0,0008 =21,25 µmol / L soit dans 22,0
mL : 21,25 10-6 x 22,0 / 1000 ~4,7 10-7 mol.
1.6. En déduire la
valeur de la concentration en moles en ions hypochlorites ClO-
dans l’eau de la fosse de plongée. Indiquer si cette eau est conforme
la législation française.
4,7 10-7 mol dans 20 mL ( 0,020 L) d'eau prélevée :
4,7 10-7 / 0,020 ~2,4 10-5 mol /L.
M(ClO-) =35,5 +16 = 51,5 g / mol.
2,4 10-5 x51,5 ~1,2 10-3 g / L ou 1,2 mg / L.
Cette valeur est comprise entre 0,4 mg.L-1
et 1,4 mg.L-1. Cette eau est donc conforme à la législation.
|
|
2. La pratique de l’apnée au NEMO 33
Lors de la pratique de l’apnée, le plongeur inspire
au maximum de sa capacité pulmonaire lorsqu’il se trouve à la surface
puis bloque sa respiration. Au cours de la descente, la pression
augmente et le volume pulmonaire diminue jusqu’à ce que la rigidité du
thorax ne permette plus
de réduire son volume : le volume pulmonaire est alors égal au volume
résiduel. Au-delà de cette profondeur, du sang est aspiré puis retenu
dans la circulation pulmonaire, remplissant ainsi les poumons. Ce
phénomène, appelé « blood shift », permet aux poumons de résister à la
compression, mais il peut aussi entraîner des troubles du rythme
cardiaque.
La capacité maximale des poumons est d’environ 6 L. Le volume résiduel,
c’est-à-dire le volume d’air contenu dans les poumons à la fin d’une
expiration forcée, est d’environ 1,5 L.
La loi fondamentale de la statique des fluides reliant la
différence de pression pA - pB entre deux points
A et B d’un fluide incompressible à ρe, g, et zA
- zB ; zA et zB étant les ordonnées
des points A et B sur un axe des z orienté suivant la verticale
ascendante s’écrit :
pA - pB = ρe g (zB - zA).
2.1. Décrire
qualitativement comment évolue la pression lorsque le plongeur descend
dans la fosse de plongée. Expliquer en quoi la loi fondamentale de la
statique des fluides rend compte de cette évolution.
Dand l'eau la pression augmente d'environ 1 bar ( 1,0 105
Pa) tous les dix mètres.
pA - pB = 103 x9,8 x10 =9,8 104
Pa ~1,0 105 Pa.
2.2. Énoncer la loi
de Mariotte relative au produit de la pression P par le volume V d’un
gaz pour une quantité de matière donnée et une température constante.
Pour une quantité de matière donnée et une température constante, le
produit de la pression par le volume du gaz est constant.
PV = Cste.
2.3. À l’aide des
données, déterminer si le phénomène de « blood shift » risque
d’apparaître lorsqu’un apnéiste, qui n’a pas expiré d’air au cours de
sa plongée, atteint le fond de NEMO 33.
Pression au fond : P = 1,0 105 +103 x9,8x35 =4,43
105 Pa = 4,43 bar.
Pression en surface : 1 bar ; volume des poumons : 6 L.
Volume des poumons au fond : V = 6 x1 / 4,43 =1,35 L, valeur inférieure
à 1,5L.
Le phénomène de « blood shift » risque d’apparaître.
Bouquet final.
On s’intéresse à différents aspects physico-chimiques d’un feu
d’artifice.
I. Aspect énergétique d’une pièce d’artifice lors de la phase ascensionnelle.
Dans cette partie, on modélise la pièce d’artifice par un point
matériel dans le référentiel terrestre supposé galiléen. La pièce
d’artifice étudiée, de masse 100 g, est tirée verticalement avec une
vitesse initiale de valeur v0 = 100 m·s-1. On étudie le mouvement de son centre d’inertie G, repéré par son ordonnée y dans un repère vertical orienté vers le haut.
On choisit l’instant t0 = 0 s lorsque le centre d’inertie G
est confondu avec l’origine du repère O. On néglige toute action
mécanique de l’air. On admet que la masse de la bombe est constante
lors de son mouvement ascendant.
En tenant compte des choix de modélisation précédents, un logiciel de
simulation permet de représenter l’évolution temporelle de l’énergie
cinétique Ec et de l’énergie potentielle de pesanteur Ep de la bombe lors de son mouvement ascendant : on obtient la représentation graphique ci-dessous.
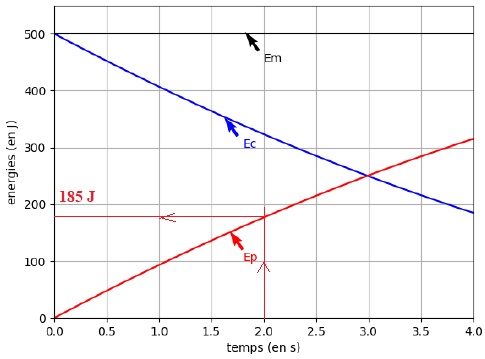
1. Après avoir
rappelé la définition de l’énergie mécanique de la pièce d’artifice,
exploiter la figure pour savoir si, dans la situation simulée,
l’énergie mécanique se conserve. Commenter le résultat obtenu.
L'énergie mécanique est la somme de l'énergie cinétique et de l'énergie potentielle.
Sur la figure, Em =Ec + Ep est représentée par un segment horizontal : l'énergie mécanique se conserve.
2. On suppose que la pièce explose à l’instant tA
= 2,0 s. Après cet instant, les évolutions de la figurene sont plus
respectées. À l’aide de la figure, déterminer la valeur de l’énergie
potentielle à cet instant puis calculer l’altitude atteinte notée yA.
Ep = 185 J ; h = Ep / (m g) =185 / (0,100 x 9,81) =1,89 102 m.
3. En réalité l’altitude maximale atteinte par la pièce vaut 55 m. Commenter l’écart observé par rapport au modèle.
Il faut prendre en compte les frottements sur les couches d'air. La masse de la bombe diminue au cours de l'ascension.
|
II. Combustion pyrotechnique
Le principe de base des feux d’artifice repose sur la combustion
de la poudre noire contenant jusqu’à 75 % en masse de salpêtre de
formule KNO3, jouant le rôle de comburant et un
mélange essentiellement constitué de carbone, mais contenant également
du soufre et des éléments métalliques pour la couleur (solides ioniques
comportant, par exemple, des ions
sodium pour le jaune ou des ions potassium pour le violet) ou pour les
effets spéciaux (métaux comme par exemple le magnésium pour des
étincelles).
Source : http://www.societechimiquedefrance.fr/feux-d-artifice.html
Afin de simplifier cette étude, on fait l’hypothèse que la combustion
de la poudre noire peut être modélisée par une seule réaction chimique
dont l’équation est :
2 KNO3 + 3 C + S ---> K2S + 3 CO2 + N2.
4. Après avoir écrit la demi-équation électronique du couple CO2 / C, préciser si le carbone joue le rôle d’oxydant ou de réducteur.
C + 2H2O---> CO2 +4H+ +4e-.
Le carbone cède des électrons, c'est un réducteur qui s'oxyde.
L’artificier prépare environ 25 g de poudre noire. Ce mélange est
réalisé dans les proportions stoechiométriques de la réaction : il
contient 3,20 g de carbone, du nitrate de potassium
(salpêtre) de formule KNO3, du soufre S et des solides ioniques ou métaux en faible quantité.
5. Déterminer la valeur de quantité de matière de carbone dans ce mélange.
n =3,20 / 12,0 ~0,267 mol.
6. En déduire la masse de nitrate de potassium nécessaire pour réaliser ce mélange.
n(KNO3) = 2 n / 3 =2 x0,267 / 3 = 0,178 mol.
(KNO3)=39,1 +14 +3x16)=101,1 g/mol.
m = 0,178 x101,1 =18,0 g.
7. En déduire le
pourcentage massique de nitrate de potassium présent dans la poudre
noire préparée et indiquer si le résultat est compatible avec la
description de la poudre noire.
18 / 25 = 0,72 (72 %).
Ecart relatif ( 75-72) / 75 ~0,04 ( 4 %).
A 4 % près ces deux résultats sont compatibles.
8. Dans les conditions de la combustion étudiée, l’énergie molaire de combustion (pour la combustion d’une mole de carbone) vaut Emcomb = – 208 kJ∙mol-1. Montrer que la valeur de
l’énergie libérée par la combustion de la poudre noire préparée par l’artificier est de l’ordre de 55 kJ.
208 x 0,267 =55,5 kJ, de l'ordre de 55 kJ.
9. Comparer la valeur précédente à l’énergie cinétique initiale de la bombe et interpréter la différence.
Ec = ½mv02 =0,5 x 0,100 x 1002 =500 J = 0,5 kJ.
La grande majorité de l'énergie de la combustion est de l'énergie
thermique. Seule une petite partie est convertie en énergie cinétique.
III. Émission lumineuse.
Les feux d’artifice émettent de la lumière selon trois phénomènes :
l’incandescence, l’émission atomique et l’émission moléculaire. On
s’intéresse uniquement à l’émission atomique dans
cette partie. Les ions des cristaux métalliques introduits sont excités
thermiquement, ce qui leur permet de passer d’un niveau d’énergie
fondamental à un niveau d’énergie supérieur ; au cours
de leur retour vers l’état fondamental, l’énergie qu’ils avaient
absorbée est émise sous forme de photons d’une longueur d’onde
caractéristique de l’élément correspondant. L’ion sodium est l’un
de ceux qui émet le plus de lumière par ce mécanisme. On donne
ci-dessous des informations concernant l’émission de lumière par le
sodium.
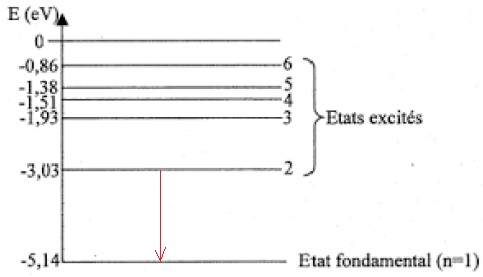
10. Sur un
diagramme de niveaux d’énergie d’un atome, comportant le niveau
fondamental et un niveau excité d’énergie supérieure, illustrer le
phénomène d’émission d’un photon.
11. Déterminer
quelle transition entre niveaux d’énergie du sodium représentés a lieu
lors de l’émission de la raie jaune du sodium, de longueur d’onde λ =
589,0 nm dans le vide.
DE = h c / l =6,63 10-34 x 3,00 108 / (589 10-9) = 3,38 10-19 J soit 3,38 10-19 / (2,6 10-19)=2,11 eV.
-5,14 +2,11 = -3,03 eV.
|
|
|


