Physique chimie, centrale �lectrique de l'ouest guyanais ( CEOG) ;
qui peut griller une tranche de pain en p�dalant ?
E3C : enseignement de sp�cialit� premi�re g�n�rale.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts.

Centrale �lectrique de l'ouest guyanais.
Le projet consiste � associer une centrale photovolta�que � une centrale � dihydrog�ne.
L’�nergie �lectrique non consomm�e produite par la centrale photovolta�que en journ�e, est utilis�e pour r�aliser l’�lectrolyse de l’eau pour produire du dihydrog�ne. Ce dihydrog�ne est alors stock� sur place pour pouvoir �tre utilis� la nuit dans une pile � combustible.
La premi�re partie de l’exercice est consacr�e � la production et au stockage du dihydrog�ne.
La deuxi�me partie est consacr�e au fonctionnement �lectrique d’un �lectrolyseur.
Partie 1. Production et stockage du dihydrog�ne.
On cherche dans un premier temps � dimensionner les diff�rents r�servoirs � utiliser pour stocker le dihydrog�ne produit par la centrale � dihydrog�ne.
Les couples d’oxydo-r�duction mis en jeu pour l’obtention de dihydrog�ne lors de l’�lectrolyse de l’eau sont les suivants :
- O2 (g) / H2O(l)
- H+  (aq) / H2 (g)
1.1. D�finir un oxydant et un r�ducteur.
Un oxydant est une esp�ce, ion ou mol�cule, susceptible de gagner un ou plusieurs �lectrons.
Un r�ducteur est une esp�ce, ion ou mol�cule, susceptible de donner un ou plusieurs �lectrons.
1.2.1. �crire les demi-�quations �lectroniques associ�es aux deux couples mis en jeu.
2H+  (aq) + 2e- = H2 (g).
�O2 (g) + 2H+  (aq) + 2e- = H2O(l).
1.2.2. L’�lectrolyse de l’eau est mod�lis�e par la r�action d’�quation :
2 H2O(l ) → 2 H2(g) + O2(g)
L’�lectrolyseur devra permettre de produire une masse de 50 kg de dihydrog�ne en journ�e.
D�terminer la valeur de la quantit� de mati�re de dihydrog�ne � produire n(H2) en journ�e.
n(H2) = 50 103 / M(H2) = 5,0 104 / 2 = 2,5 104 mol.
1.2.3. Calculer la masse d’eau m(H2O) n�cessaire pour produire les 50 kg de dihydrog�ne � stocker durant la journ�e.
n(eau) = n(H2) ; masse d'eau : 2,5 104 x M(H2O) = 2,5 104 x18 = 4,5 105 g = 4,5 102 kg.
1.2.4. D�terminer le volume minimum du r�servoir d’eau V(H2O).
m(eau) / masse volumique de l'eau = 450 / 1000 = 0,45 m3.
1.3.1. Le stockage du dihydrog�ne s’effectue quant � lui g�n�ralement avec des bouteilles ou assemblages de bouteilles cylindriques, en acier, port�es � une pression Pstock de 5,0�10 6 Pa.
En utilisant la loi de Mariotte, d�terminer le volume n�cessaire Vstock des bouteilles pour stocker le dihydrog�ne.
P V = Constante ( loi de Mariotte).
Pstock Vstock =Patm n(H2)Vm.Vstock =Patm n(H2)Vm / Pstock= 1,0 105 x 24  10-3 x 2,5 104 / (5,0 106) =12 m3.
1.3.2. Commenter les r�sultats sachant que le parc photovolta�que s’�tend sur une surface de 700 000 m �.
Le volume de stockage du dihydrog�ne est tr�s faible, compar� � l'�tendue du parc photovolta�que.

Partie 2. �tude du fonctionnement �lectrique d’un �lectrolyseur.
On cherche maintenant � caract�riser le fonctionnement �lectrique d’un �lectrolyseur pouvant servir � produire du dihydrog�ne.
L’�lectrolyse de l’eau est r�alis�e au laboratoire � l’aide du montage �lectrique suivant.
En faisant varier la tension U aux bornes de l’�lectrolyseur, on mesure pour chaque valeur de la tension U, l’intensit� du courant I dans le circuit de l’�lectrolyseur.
La caract�ristique repr�sentant l’�volution de la tension U aux bornes de l’�lectrolyseur en fonction de l’intensit� du courant I, est repr�sent�e ci-dessous.

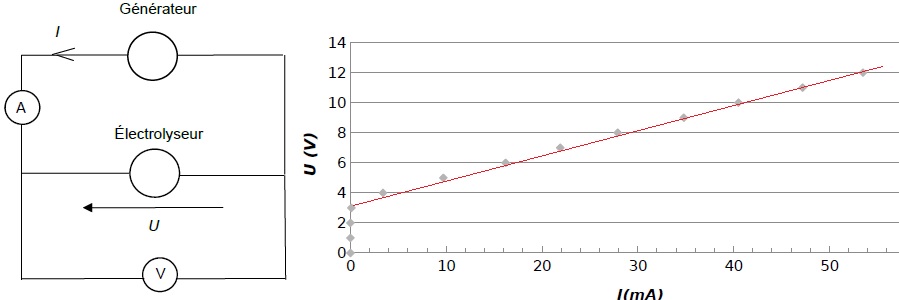
Une partie de la courbe obtenue est mod�lisable par l’�quation U = E’ + r’.I o� :
 E’ est la force contre-�lectromotrice de l’�lectrolyseur exprim�e en volt (V) ;
 r’ est la r�sistance interne de l’�lectrolyseur exprim�e en ohm (W).
�quation de la droite d�termin�e � l’aide d’un logiciel de calcul : U = 3,46 + 160 � I o� U exprim�e en V et I en A.
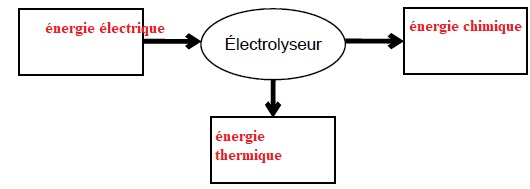
2.1. Donner la forme d’�nergie � faire appara�tre dans chaque cadre de la cha�ne �nerg�tique suivante :

2.3.1. Donner l’expression litt�rale de l’�nergie totale re�ue Ere�ue par l’�lectrolyseur s’il fonctionne pendant une dur�e Dt en fonction de U, I et Dt.
Ere�ue = U I Dt.
2.3.2. Donner l’expression litt�rale de l’�nergie totale dissip�e Edissip�e par l’�lectrolyseur sous forme d’effet Joule s’il fonctionne pendant une dur�e Dt.
Erdissip�e = r I2 Dt.
2.3.3. En d�duire que l’expression litt�rale du rendement de l’�lectrolyseur est η = E' / U.
Energie utile = E' I Dt.
Rendement = �nergie utile / �nergie consomm�e = E' I Dt / (U I Dt) = E' / U
2.3.4. Calculer le rendement de cet �lectrolyseur pour un courant d’intensit� I = 50 mA.
U = 3,46 + 160 � I  = 3,46 + 160 x 0,050 = 11,46 V.
Rendement : 3,46 / 11,46 ~0,30 ( 30 %).
2.4. En s’appuyant sur les donn�es de l’�nonc� et les r�ponses aux questions pr�c�dentes, expliquer en quoi le projet semble �tre une bonne alternative aux �nergies fossiles.
La production �lectrique ( 10 MW le jour et 3,0 MW la nuit ) est stable  et �quivalente � la production des centrales thermiques fonctionnant au diesel ou au gaz. Le prix de l'�lectricit� est inf�rieur � celui des centrales thermiques. De plus, il n'y a pas de pollution, pas de logistique d'approvisionnement en carburant.


Qui peut griller une tranche de pain en p�dalant ?
L’�nergie musculaire du cycliste est transform�e en �lectricit� gr�ce � une dynamo actionn�e par la rotation du p�dalier. L’ensemble alimente un grille-pain. Pour que l’appareil fonctionne, il faut que le champion produise une puissance de 700 W. Deux minutes plus tard, le cycliste a fourni au
grille-pain 0,021 kWh (76 kJ) suffisant pour sortir une tranche l�g�rement brunie.
1. Performance de Robert F�rstemann.
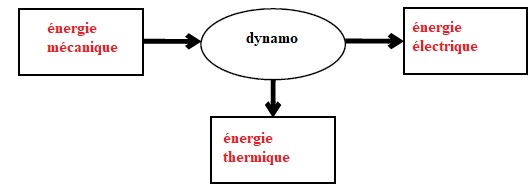
1.1. Sch�matiser la cha�ne �nerg�tique de la dynamo du v�lo utilis� par Robert F�rstemann.
On suppose que le rendement de cette dynamo n’est pas de 100 %.

1.2. Le grille-pain est con�u pour fonctionner normalement sous une tension de 230 V et pour fournir une puissance de 700 W. Montrer que la valeur de l’intensit� du courant qui traverse le grille-pain en fonctionnement normal est d’environ 3 A.
I = P / U = 700 / 230 =,04 ~3,0 A.
1.3.Nommer l’effet responsable de l’�l�vation de temp�rature dans le grille-pain. D�duire de la question pr�c�dente la valeur de la r�sistance R du circuit �lectrique de cet appareil.
Le pain est chauff� par effet Joule.
P = R I2 ; R = P / I2 = 700 / 3,02 ~77,8 ~78 ohms.
Une simulation de la caract�ristique du circuit �lectrique du grille-pain est donn�e ci-dessous.

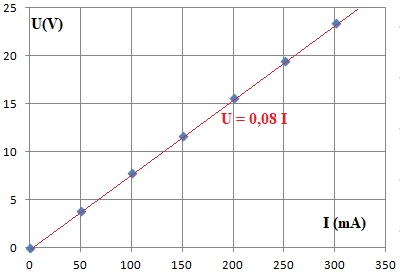
Elle relie la tension U appliqu�e � l’intensit� du courant �lectrique I qui traverse le circuit �lectrique du grille-pain.
1.4. Indiquer la loi qui mod�lise la caract�ristique du circuit �lectrique du grille-pain, retrouver la valeur de la r�sistance du circuit �lectrique du grille-pain et comparer le r�sultat � celui de la question pr�c�dente.
Loi d'Ohm U = R I = 0,08 I avec U en V et I en mA.
R = 0,08 kW= 80 ohms.
Ecart relatif ( 80 -78) / 78 ~0,03 ( 3 %).
Les deux r�sultats sont en accord.
1.5. D�terminer la valeur de la puissance moyenne fournie par Robert Forstemann. Estimer, en prenant R = 76 Ω, la valeur moyenne de la tension et de celle de l’intensit� du courant de fonctionnement du grille-pain durant la performance. Commenter.
Pmoyenne =  �nergie (J) / dur�e (s) = 76 103 / (2 x60) ~6,3 102 W.
P = U I avec U = R I ; P = R I2 ; I =(P / R)� =(6,3 102 / 76)�~ 2,9 A ; U = 76 x 2,9 ~2,2 102 V.
1.6. Estimer, en effectuant un bilan �nerg�tique, la valeur de la vitesse maximale que pourrait atteindre le cycliste � v�lo initialement immobile en 5 secondes sur un terrain plat en d�veloppant une puissance de 630 W. Commenter.
Energie mise en oeuvre : 630 x 5 = 3 150 J.
Cette �nergie est convertie en �nergie cin�tique : �mv2  = 3150 avec m = 60 kg par exemple.
v2 = 2 x 3150 / 60 =105 ; v ~10 m /s. ( 36 km / h).

 


2. R�cup�rer apr�s l’effort
Apr�s un effort intense, tel que celui fourni par Robert F�rstemann, l'organisme a besoin de glucides simples tels que le saccharose, appel�s sucres rapides, disponibles rapidement pour
reconstituer les ressources en �nergie de l'organisme. Dans cette partie, nous cherchons � d�terminer la quantit� n�cessaire de sucre (saccharose) � ing�rer pour r�cup�rer apr�s l’effort
fourni par Robert F�rstemann.
Le saccharose, sucre de table habituel, est un compos� organique de formule brute C12H22O11.
Son assimilation par l’organisme s’effectue apr�s son hydrolyse (r�action avec l’eau du saccharose) qui forme du glucose et du fructose, deux sucres de m�me formule brute.
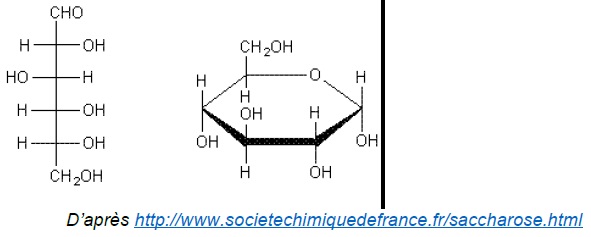
La mol�cule de glucose peut adopter une configuration � cha�ne ouverte ou cyclique, comme l’illustre les deux repr�sentations du glucose suivantes :

2.1. Le spectre infrarouge obtenu par analyse d’un �chantillon de glucose est fourni ci-dessous.
D�duire de ce spectre la configuration majoritaire du glucose dans l’�chantillon �tudi�. Justifier.

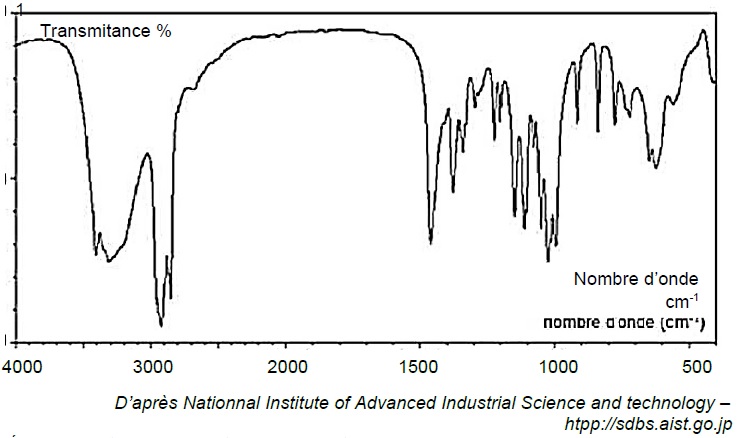
L'absence du pic caract�ristique du groupe carbonyle C=O vers 1700 cm-1, implique que la forme cyclique du glucose est tr�s majoritaire.
2.2. �crire l’�quation de la r�action mod�lisant l’hydrolyse du saccharose.
C12H22O11 + H2O ---> 2 C6H12O6.
2.3.V�rifier que l’oxydation compl�te d’un morceau de sucre lib�re une �nergie d’environ 24 kcal.
L’�nergie molaire fournie par la combustion (oxydation compl�te) du saccharose est 5,8�106 J�mol-1 ;
une bo�te de sucre de masse nette m = 1,0 kg contient 168 morceaux ; masse d'un morceau de sucre : 1000 / 168 = 5,92 g.
Quantit� de mati�re = 5,92 / M(saccharose) = 5,92 / (12 x12 +22 +11 x16) = 5,92 / 342 =0,0173 mol.
Energie correspondante : 0,0173 x 5,8 106 =100 398 J ~ 100,4 kJ soit 100,4 / 4,18 = 24 kcal.
2.4.En d�duire la quantit� de sucre que Robert F�rstemann doit ing�rer pour compenser l’effort r�alis� en supposant que l’�nergie musculaire a �t� int�gralement transf�r�e au grillepain.
Commenter.
Energie consomm�e en p�dalant : 76 kJ.
Energie fournie par l'oxydation d'un morceau de sucre : 24 kcal soit 24 x4,18 ~100 kJ.
Il lui faudrait consommer environ les 3 / 4 d'un morceau de sucre.
Dans la r�alit�, toute l'�nergie musculaire n'est pas transf�r�e au grille-pain. Il lui faudra donc sans doute consommer plusieurs morceau de sucre pour r�cup�rer.


  

menu