Physique chimie, ressources d'énergie renouvelables ; vélo à assistance électrique. E3C : enseignement de spécialité première générale. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Ressources d'énergie renouvelables. I. Étude du stockage chimique de l’énergie. Le Professeur K. Hashimoto (Université de Sendai, Japon) a développé un procédé qui transforme le dioxyde de carbone en méthane en utilisant un électrolyseur à eau de mer et des catalyseurs. Les électrolyseurs sont alimentés par l’énergie solaire. Le méthane produit peut ensuite servir de carburant afin de faire fonctionner un générateur électrique. Ce dernier fonctionne sur le principe suivant : l’énergie thermique libérée par la combustion du méthane permet de produire de la vapeur d’eau qui actionne une turbine. Un alternateur permet alors de produire de l’électricité. 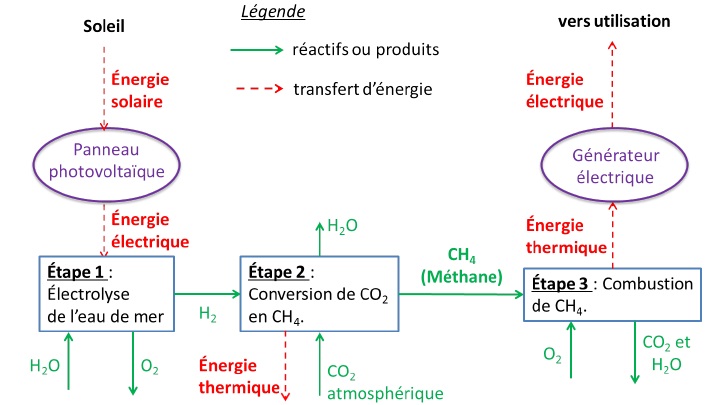Il se produit dans les différentes étapes les transformations chimiques modélisées par les réactions chimiques d’équation : - étape 1 :H2O(l) ---> H2 (g) + ½O2(g). - étape 2 : CO2(g) + 4H2(g) ---> CH4(g) + 2H2O(g). - étape 3 : combustion complète du méthane. Problématique 1 : en quoi le procédé de transformation du dioxyde de carbone en méthane peut-il permettre de répondre aux difficultés liées au caractère intermittent des énergies renouvelables ? 1. Justifier pour chacune des étapes 2 et 3 du procédé si elle est endothermique ou exothermique. Ces deux étapes libèrent de l'énergie thermique : elles sont exothermiques. 2. Écrire l’équation de la réaction de combustion complète du méthane de formule brute CH4. CH4(g) + 2O2(g) ---> CO2(g) + 2H2O(g). On cherche à estimer le pouvoir calorifique massique du méthane. Pour cela on mesure la masse de méthane nécessaire pour porter à l’ébullition une masse d’eau meau = 1,00 kg dont la température initiale est Ti = 20,2 °C. La manipulation est réalisée 6 fois avec le même dispositif. On rappelle que le pouvoir calorifique massique du méthane est défini par la relation : PC = Elibérée / mméthaneconsommée avec Elibérée l’énergie libérée lors de la combustion d’une masse de méthane mméthane. Les résultats sont reportés dans le tableau ci-dessous. essai n°1 n°2 n°3 n°4 n°5 n°6 mméthane consommé (g) 12,1 10,9 11,6 11,0 11,8 10,9 L’énergie libérée par la combustion peut être déterminée par la relation : Elibérée =meau ceau (Tf-Ti) avec : - ceau la capacité thermique massique de l’eau liquide : ceau = 4,18 kJ·kg-1·K-1. - Tf la température finale de l’eau, c’est-à-dire la température d’ébullition de l’eau dans les conditions de l’expérience Tf = 100,0 °C. Pour effectuer le calcul du pouvoir calorifique massique à partir des résultats expérimentaux, il est nécessaire de déterminer une masse expérimentale de méthane consommée. Pour cela, on fait la moyenne sur toutes les valeurs de masse (valeurs n°1 à n°6). 3. Montrer, en détaillant les calculs, que la valeur expérimentale obtenue pour le pouvoir calorifique massique PC du méthane est de l’ordre de 29 MJ·kg-1. Elibérée =1,00 x4,18 x(100-20,2)=333,56 kJ. Moyenne des masse de méthane : (12,1 +10,9 +11,6 +11,0 +11,8 +10,9) / 6 =11,38 g PC = 333,56 / (11,38 10-3) =29 311 kJ ~ 29 MJ kg-1. La valeur de référence du pouvoir calorifique massique du méthane est 50 MJ·kg-1. 4. Proposer une explication pour interpréter l’écart entre la valeur expérimentale du pouvoir calorifique massique du méthane et sa valeur de référence. L'énergie libérée par la combustion sert aussi à chauffer le récipient et l'air environnant. On considère que : - la production d’un kilogramme de méthane par les étapes 1 et 2 du procédé nécessite 117 MJ d’énergie intermittente ; - seuls 25 % de l’énergie thermique libérée par la combustion du méthane est transformée en électricité. 5. Répondre à la problématique 1 en déterminant la proportion d’énergie intermittente pouvant être considérée comme ayant été stockée par ce procédé. On utilisera la valeur de référence du pouvoir calorifique massique du méthane. Energie électrique produite : 50 x0,25 =12,5 MJ. Proportion d'énergie intermittente stockée : 12,5 / 117 ~0,107  ( ~ 11 %). II. El Hierro : île pionnière de l’énergie renouvelable Le pompage-turbinage est une technique de stockage de l’énergie électrique permettant de palier l’intermittence des ressources d’énergie renouvelables. Lorsque les conditions météorologiques sont favorables, l’excédent d’énergie produit par les éoliennes est utilisé pour faire fonctionner des pompes permettant de remplir des retenues d’eau situées en altitude. Lorsque la production d’électricité devient insuffisante, les retenues d’eau sont ouvertes. Après une chute de 650 m à travers une conduite forcée, l’eau actionne des turbines hydroélectriques qui entrainent un alternateur afin de produire de l’électricité. Problématique 2 : en quoi les infrastructures de l’île de El Hierro lui permettent-elle de s’affranchir des énergies fossiles ? On s’intéresse à l’eau contenue dans le réservoir supérieur qui chute à travers la conduite forcée pour remplir le bassin inférieur. Le volume d’eau utile considéré est donc égal au volume du réservoir inférieur Vinf et la masse de ce volume d’eau utile, notée M, chute via la conduite du point A au point B. 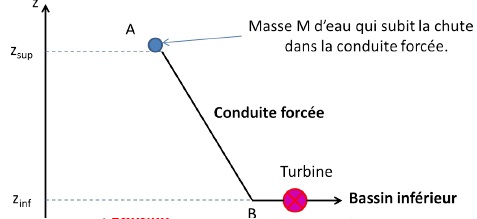Données : - altitude du bassin supérieur : zsup = 700 m - volume du bassin inférieur : Vinf = 150 000 m3 - altitude du bassin inférieur : zinf = 50,0 m - accélération de la pesanteur : g = 9,81 m.s-2 - masse volumique de l’eau : ρeau = 1000 kg.m-3 - consommation annuelle sur l’île d’El Hierro en 2018 : E = 42,0 GWh - 1,000 Wh = 3600 J. On se place dans le référentiel terrestre, supposé galiléen, muni d’un axe Oz orienté vers le haut. L’énergie potentielle de pesanteur est prise nulle à l’altitude z = 0. 6. Exprimer la variation de l’énergie potentielle de pesanteur ΔEpp de cette masse M d’eau lors de sa chute à travers la conduite forcée, en fonction de ρeau, Vinf, g, zsup et zinf. Montrer que la valeur de ΔEpp est de l’ordre de − 950 GJ. ΔEpp = Mg(zinf-zsup) = Vinf ρeau g (zinf-zsup) =150 000 x 1000 x9,81 x(50,0-700) ~ -9,56 1011 J soit -956 GJ. 7. En considérant que l’eau est immobile dans le réservoir supérieur et que la chute à travers la conduite s’effectue sans frottement, déterminer la valeur de l’énergie cinétique de cette masse M d’eau lorsqu’elle actionne les turbines. L'énergie mécanique initiale est sous forme potentielle de pesanteur ; l'énergie mécanique finale est sous forme cinétique. En absence de frottements, l'énergie mécanique se conserve. Energie cinétique finale = 956 GJ. 8. Sachant que le rendement de la phase de turbinage est de 90 %, calculer la valeur de l’énergie électrique que peut fournir la centrale hydro-électrique. 956 x 0,90~860 GJ. 9. Répondre à la problématique 2 en déterminant le nombre de jours d’autonomie sans vent que représente la réserve d’eau des bassins. 42,0 GWh soit 42,0 x 3600 =1,512 105 GJ par an. 1,512 105 / 365 ~4,1 102 GJ par jour. Nombre de jours d'autonomie sans vent : 860 / (4,1 102) ~ 2 jours.   Vélo à assistance électrique (10 points) Afin d’alimenter le moteur de l'assistance d’un vélo électrique, un spécialiste propose plusieurs batteries lithium–ion. Elles délivrent toutes une tension nominale de 36 V. En revanche leurs capacités varient de 8,7 A.h à 17,4 A.h en fonction du modèle choisi. Le courant électrique à l’extérieur de la batterie lithium-ion est engendré par la circulation d'électrons entre les deux électrodes de la batterie : - une électrode négative qui est le siège de la réaction électrochimique suivante : Li → Li++ e- - une électrode positive qui est le siège de la réaction électrochimique suivante: CoO2 + Li++ e- → LiCoO2. Li symbolise l'élément lithium et Co l'élément cobalt. Lors du fonctionnement de la batterie, les ions Li+ traversent le séparateur suivant le sens des flèches représenté dans le schéma ci-dessous. 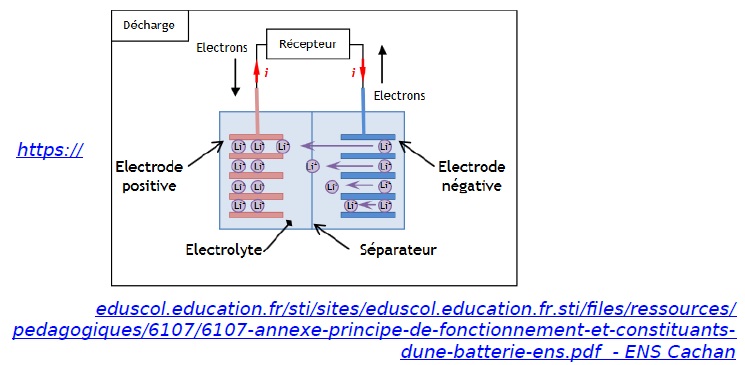1. Quel est le couple oxydant-réducteur mis en jeu à l’électrode négative ? Li+ / Li. 2. La réaction électrochimique à cette électrode est-elle une oxydation ou une réduction ? Justifier. Le métal lithium libère des électrons ; il s'oxyde. II. Bilan énergétique pour une batterie de 14,5 A.h. 3. Déterminer la valeur de l'énergie potentielle de pesanteur emmagasinée par le système "vélo électrique + cycliste" lorsque le cycliste effectue le dénivelé ascensionnel positif maximal ( 1450 m) correspondant à l’autonomie de la batterie. Masse cycliste + vélo : m = 90 kg. Epp = mgh = 90 x 9,81 x1450 ~ 1,28 106 ~1,3 106 J~1,3 MJ. 4. D’après les données constructeur, ce type de batterie délivre au maximum une énergie maximale Emax = 1,88.106 J = 1,88 MJ. 4.1. En théorie, Emax permet-elle d'effectuer le dénivelé ascensionnel indiqué ? Oui, 1,88 MJ est supérieur à 1,3 MJ. 4.2. Dans les conditions réelles, un cycliste en forme moyenne doit fournir en pédalant 50% de l'énergie nécessaire à l'ascension. Pourquoi faut-il apporter une énergie supérieure à l'énergie potentielle de pesanteur pour réaliser l'ascension ? Une partie de l'énergie fournie est dissipée en chaleur lors des frottements roue -sol. Il faut aussi prende en compte les frottements sur les couches d'air. 5. Compléter la chaîne énergétique  à l'aide des mots suivants : transfert thermique ; transfert mécanique ; transfert électrique ; énergie chimique ; énergie mécanique ; énergie thermique. 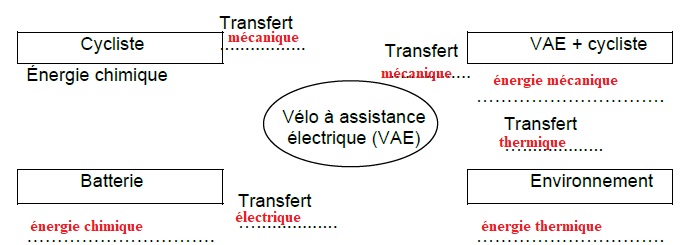III.Transformation du glucose dans le muscle : comment le muscle du cycliste produit-il de l’énergie ? Au cours de l’effort sportif, le glucose est dégradé par l’organisme en acide pyruvique. Selon les conditions d’oxygénation du cycliste, l’acide pyruvique sera dégradé à son tour soit en dioxyde de carbone et en eau (en milieu aérobie), soit en acide lactique (en milieu anaérobie). 6. Quel est le nom des familles de fonctions correspondant aux deux groupes caractéristiques de l’acide pyruvique ? 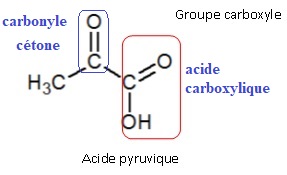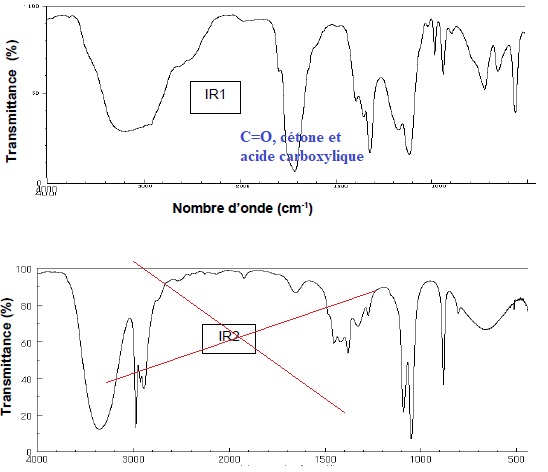7. Parmi les spectres IR (IR1 et IR2) proposés ci-dessous, choisir, en justifiant, celui correspondant à l’acide pyruvique. En milieu aérobie (présence de dioxygène), la transformation chimique du glucose dans un muscle peut être modélisée par la réaction d’équation : C6H12O6(aq) + 6 O2(g) ---> 6 CO2(g) + 6 H2O(l) L’énergie libérée par cette réaction est de 673 kcal pour une mole de glucose consommée par le muscle. 8. Calculer la valeur de la quantité de matière de glucose consommée par les muscles du cycliste afin de libérer une énergie Emusc = 640 kJ pour effectuer l’ascension maximale. 1 kcal = 4,18 kJ ; 673 x4,18 ~2813 kJ mol-1. 640 / 2813 =0,2275 ~0,228 mol de glucose. 9. On suppose que la transformation chimique est totale. Compléter le tableau d’avancement  et calculer les valeurs de la masse de glucose et du volume de dioxygène consommés pour effectuer l’ascension. C6H12O6 +6O2 ---> 6CO2 +6H2O initial (mol) 0,228 excès 0 solvant final (mol) 0 6 x0,228 =1,365 ~1,37 Masse de glucose : 0,2275 x M(glucose) = 0,228 x 180 =40,95 ~41,0 g. Quantité de matière de dioxygène : 6 x0,2275 =1,365 mol. Volume molaire des gaz dans les conditions de l'expérience : 24,0 L / mol. Volume de dioxygène : 1,365 x24,0 ~32,8 L.

menu