Mathématiques
: contrôle continu première technologique
20 / 01 / 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
.
.....
|
Exercice2.
5 points.
On
s'intéresse à la population d'une ville et on étudie plusieurs modèles
d'évolution de cette population. En 2018, la ville comptait 15 000
habitants.
1. Modèle 1.
On fait l'hypothèse que le nombre d'habitants augmente de 1000 par an.
On note un le nombre d'habitants pour l'année 2018 +n. Ainsi u0 = 15 000.
a. Calculer u1 et indiquer ce que représente u1.
u1 = u0 +1000 = 15 000 + 1000 = 16 000
En 2019 la ville compte 16 000 habitants.
b. Donner la nature de la suite sans justification.
Suite arithmétique.
c. On considère l'algorithme ci-dessous :
N=0
U=15000
while U < 30000 :
U = U+1000
N=N+1
A la fin de l'exécution de cet algorithme N = 15.
Interpréter cette valeur dans le contxte de l'exercice.
En 2018+15 = 2033, la ville comptera 33 000 habitants.
2. Modèle 2.
On fait l'hypothèse que le nombre d'habitants augmente de 4,7 % par an. On note vn le nombre d'habitants pour l'année 2018+n.
Ainsi v0 = 15 000.
a. On admet que la suite est géométrique. Déterminer sa raison.
100 + 4,7 = 104,7.
Le coefficient multiplicateur ( raison) est égal à 1,047.
b. Calculer selon ce modèle, le nombre d'habitants en 2023 ( arrondir à l'unité).
2019
|
2020 |
2021
|
2022 |
2023
|
15 000 x1,047=15 705
|
15705 x1,047 =16443
|
17 216
|
18 025
|
18872
|
.
|
| ..
... |
.
.
|
Exercice 3 ( 5 points).
On considère la fonction f définie sur [-4 ; +4] par f(x) = x2-2x-3.
1. Calculer l'image de -1 par f.
f(-1) = (-1)2-2(-1)-3 =1+2-3=0.
2. Montrer que 3 est solution de f(x) = 0.
f(3) = 32 -2 *3 -3 = 9-6-3=0.
3. Donner une forme factorisée de f(x).
f(x) = (x-3)(x-(-1)) =(x-3)(x+1)..
4. Dresser le tableau de signes de f sur cet intervalle.
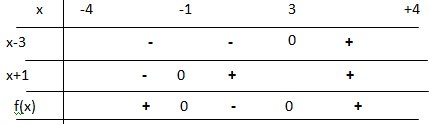
5. Déterminer quelle courbe représente la fonction f. Justifier.
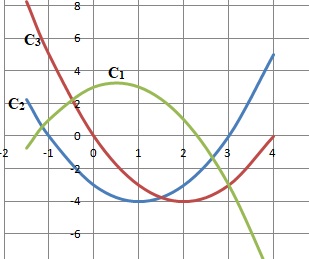
C1 ne convient pas : elle est positive sur [-1 ; 2 ].
C3 ne convient pas : elle est négative sur [0 ; 4 ].
C2 convient : elle est négative sur [-1 ; 3 ].
.
|
| .
. |
Exercice 4. ( 5 points).
Dans
un club multisport de 400 adhérents, le tennis, le squash et le
badminton sont pratiqués. Les adhérents sont classés suivant leurs
catégories : enfant; senior, vétéran.
15 % pratiquent le badmington et parmi ceux-là, le tiers sont des enfants.
75 % pratiquent le tennis et parmi eux, 32 % sont des seniors.
Parmi les adhérents pratiquant le squash, aucun n'est enfant et 20 sont des vétérans.
1. Compléter le tableau suivant :
|
Badminton
|
Tennis
|
Squash
|
Total
|
Enfant
|
20
|
130
|
0
|
150
|
Senior
|
30
|
96
|
20
|
146
|
Vétéran
|
10
|
74
|
20
|
104
|
Total
|
60
|
300
|
40
|
400
|
Dans les questions suivantes, les résultats seront donnés sous forme de fractions irréductibles.
2. On choisit au hasard un adhérent parmi les 400 adhérents du club.
On considère les événements suivants :
E : " l'adhérent est un enfant".
S : " l'adhérent est un senior".
V: "l'adhérent est un senior".
T :" l'adhérent joue au tennis".
D : " l'adhérent joue au squash".
B : " l'adhérent joue au badminton".
a. Déterminer la probabilité des événements S et T.
P(S) = 146 / 400 =73 / 200.
P(T) = 300 / 400 = 3 / 4.
b. Décrire à l'aide d'une phrase l'événement S n T puis calculer sa probabilité.
L'adhérent est un senior qui joue au tennis.
P(S n T) = 96 / 400 = 24 / 100 =6 /25.
3. On choisit au hasard un adhérent parmi les joueurs de badminton. Calculer la probabilité que ce soit un vétéran.
PB (V) = 10 / 60 = 1 / 6.
4. Calculer la probabilité conditionnelle de E sachant T, notée PT(E).
PT(E) = 130 / 300 = 13 / 30.
|
.
|
|