Mathématiques : contrôle continu première technologique 20 / 01 / 2020

Mathématiques : contrôle continu première technologique 20 / 01 / 2020.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.

.....

Automatismes.
Sans calculatrice. Durée 20 minutes.
1. Résoudre dans R l'équation : 3x-5 = 7.
3x = 7+5 ; 3x = 12 ; x = 12 / 3 ; x = 4.

2. Une veste coûte 80 €.On obtient une remise de 20 % sur son prix. Quel est le montant de la remise ?
80 x20 / 100 = 16 €.

3. Le chiffre d'affaire d'une entreprise pour l'année 2019 est de 10 000 €. Le chef d'entreprise prévoit une diminution de 5 % de ce chiffre en 2020. Calculer le chiffre prévisible en 2020.
100-5 = 95.
Coefficient multiplicateur : 0,95.
10 000 x 0,95 = 9500 €.

4. Développer et réduire : (x-3)².
(x-3)(x-3) = x² -3x-3x+9=x² -6x+9.

5. Quel est le signe de la fonction affine f définie par : f(x) = -2x+8 lorsque x >4 ?
f(x) = 0 ; -2x+8=0 ; 2x = 8 ; x = 4.
Le coefficient de x est négatif : f(x) est décroissante.
f(4) = 0; pour x > 4, f(x) est négative.

6. Exprimer sous forme d'une puissance de 2 :
2¹⁰ / (2 x2³)=2¹⁰ / 2⁴ = 2^10-4 = 2⁶.

7. Déterminer la valeur de l'entier n tel que : 10ⁿ <2019 <10ⁿ⁺¹.
1000 < 2019 < 10000 ; 10³ <2019 <10⁴. n=3.

8. Soit la fonction définie par f(x) = 3x²+1. Calculer l'image de 2 par f.
f(2) =3*2²+1 = 3 *4 +1 =12+1=13.

9. Peut-on dire que la droite d'équation y = 3x-1 passe par le point de coordonnées (2 ; 1) ?
3x-1 =3*2-1 = 6-1 = 5 différent de 2.
La droite ne passe pas par ce point.

10. On considère la fonction représentée par la courbe ci-dessous. Lire l'image de -1 par f.

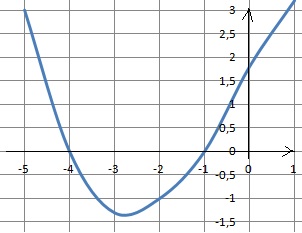f(-1) ~ 0.

.. ...

. .

Partie II. Avec calculatrice.
Exercice 2 ( 5 points).
En 2019, Adam est embauché par une entreprise qui lui propose un salaire mensuel net de 1500 €.
Son salaire net augmentera de 50 € au premier janvier de chaque année suivante.
On note u la suite qui modèlise le salaire mansuel au cours de l'année 2019 +n.
Ainsi u(0) = 1500 et u(1) = 1550.
1. Calculer le salaire mensuel net en 2021.
u(2) = u(1) +50 = 1550 +50 = 1600 €.
2. Etablir une relation entre u(n+1) et u(n) et préciser la nature de la suite.
u(n+1) = u(n) +50 ; suite arithmétique.
3. Quel est le sens de variation de la suite ? Justifier.
u(n+1) -u(n) = 50, valeur positive.
u(n+1) > u(n), suite croissante.
Au cours de l'année 2019, Alice est embauchée par une entreprise qui lui propose un salaire mensuel net de 1400 €.
Son salaire net augmentera de 4 % au premier janvier da chaque année suivante.
On note v la suite qui modèlise le salaire net d'Alice au cours de l'année 2019 +n.
4. Quelle est la nature de la suite v ?
Suite géométrique.
v(n+1) = 1,04 v(n) avec v(0) = 1400.
5. A partir de quelle année le salaire d'Alice dépassera t-il pour la première fois celui d'Adam ?

n
2019 (n = 0)
n=1 (2020)
n=2 (2021)
n=3 ( 2022)
n=4 (2023)
2024
2025
2026
2027

u(n)
1500
1500 +50 = 1550
1550 +50 =1600
1600+50=1650
1700
1750
1800
1850
1900

v(n)
1400
1400 x1,04 =1456
1456 x1,04 =1514,24
1514,24 x1,04=1574,81
1637,8
1703,31
1771,44
1842,30
1916

.

.
.

Exercice 3. ( 5 points).
On considère la fonction f définie sur l'intervalle [-2 ; 4]. Sa courbe représentativeC est une parabole.

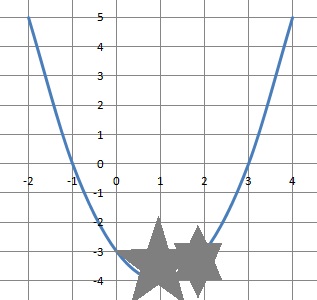
Une tache d'encre masque une partie de la courbe.
1. Lire sur le graphique l'image de -1 et de 3 par f.
f(-1) =0 ; f(3) =0.
2. Résoudre par lecture graphique sur l'intervalle [-2 ; 4], l'inéquation f(x) < 0.
x appartient à [-1 ; 3 ].
3. On admet que l'expression de la fonction f est de la forme f(x) = (x-x₁)(x-x₂) avec x₁ < x₂. Préciser les valeurs de x₁ et x₂.
f(x) = (x-x₁)(x-x₂) = 0 conduit à :
x-x₁ =0 soit x = x₁ = -1 et à x-x₂ =0 soit x = x₂ = 3.
Par suite f(x) = (x-(-1))(x-3)=(x+1)(x-3) = x² -3x+x-3 = x² -2x-3.
4. Retrouver les coordonnées du sommet de la parabole.
La courbe est symétrique par rapport à la droite d'équation x = 1.
Ou bien x = -b / (2a) = -(-2) / (2 *1) = 1.
f(1) = 1²-2*1-3 = -4.
5. Dresser le tableau de variations de f. On admet que f(-2) = f(4) = 5.

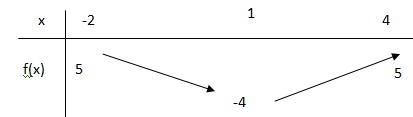
Exercice 4. (5 points).
Un match de rugby entre deux équipes A et B se déroule dans un stade accueillant 75 000 spectateurs.
52500 supportent l'équipe A.
32250 sont licenciés à la FFR.
13125 supporters de l'équipe A sont licenciés à la FFR..
1. Compléter le tableau suivant :

Licencies à la FFR
non licencies à la FFR
Total

Supporter de l'équipe A
13 125
39 375
52 500

Supporter de l'équipe B
19 125
3 375
22 500

Total
32 250
42 750
75 000

2. On interroge au hasard un spectateur et on considère les événements suuivants :
A : " le spectateur est un supporter de l'équipe A".
B : " le spectateur est un supporter de l'équipe B".
L : " le spectateur est licencié à la FFR".
Calculer les probabilités suivantes.
P(B) =22 500 / 75 000 = 0,3.
Décrire l'événement A n L.
Le spectateur est licencié à la FFR et supporte l'équipe A.
Calculer P(A n L).
P(A n L) = 13 125 / 75000 =0,175.
3. On interroge au hasard un spectateur. C'est un supporter de l'équipe B. Calculer la probabilité qu'il soit licencié à la FFR.
19 125 / 22 500 =0,85.

menu