Trigonométrie,
classe de première technologique.
.
.
|
|
1. Donner l'écriture principale des angles suivants.
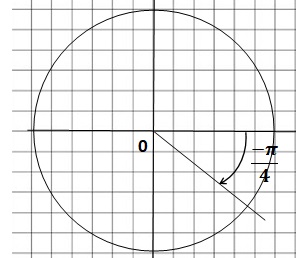
a. 15 p / 4.
15 / 4 = 3,75 = 2 x2 -0,25.
15 p / 4 =2 x2 p - 0,25 p = 2 x2 p - p / 4. Réponse : - p / 4.
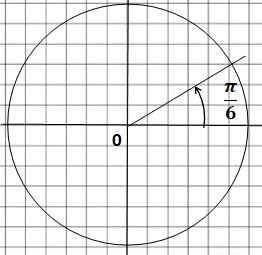
b. 13 p / 6.
13 / 6 ~ 2,17 = 2 x1 +0,17 = 2 x1 +1 / 6
13 p / 6 =2 p + 0,17 p = 2 p + p / 6. Réponse : p / 6
. 
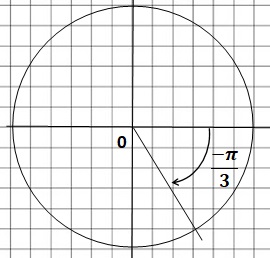
c. 17 p / 3.
17 / 3 ~ 5,67 = 3 x 2 -0,33 = 3 x2 -1 / 3
17 p / 3 =3 x 2 p - 0,33 p = 3 x 2 p - p / 3. Réponse : - p / 3.
|
2. On donne sin (p/3) ~0,866 et cos (p/3) = 0,5
2.a. Exprimer sin (-p/3) et sin (2p/3) en fonction de sin (p/3).
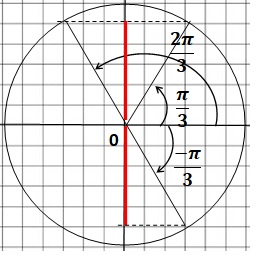
sin (-p/3) = -sin (p/3) et sin (2p/3) = sin (p/3).
2.b. Exprimer cos (5p/6) et cos (-p/6) en fonction de sin (p/3).
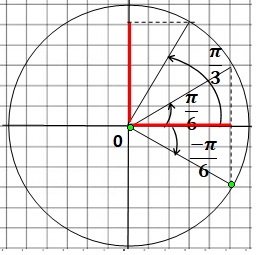
cos (-p/6) = cos (p/6) = sin (p/3).
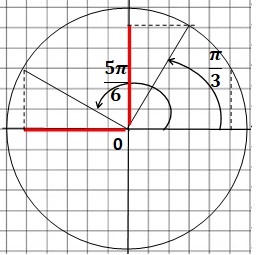
cos (5p/6) = - sin (p/3).
|
3.a. Déterminer l'angle a tel que : cos a = 0,5 ; a appartient à ] -p ; + 2p]
0,5 = cos ( p/3).
cos a = cos ( p/3).
a = p/3 + 2kp et a = -p/3 + 2kp.
k = 0 ; a = p/3 ; a = - p/3 ;
k = 1 : -p/3 + 2p = 5p/3.

b. Déterminer l'angle a tel que : sin a = -0,5 ; a appartient à ] -2p ; +p]
-0,5 = sin ( -p/6).
sin a = sin ( -p/6).
a = -p/6 + 2kp et a = p+p/6 + 2kp = 7p/6 + 2kp.
k = 0 ; a = -p/6 ;
k = -1 : 7p/6 - 2p = -5p/6.

4. Calculer sin (x) sachant que :
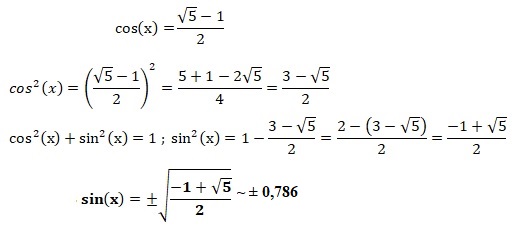
|
|