Spécialité Mathématiques, classe de première 2021.

Exercice 1. QCM.
1. Soit f la fonction définie sur R par f(x) =(x+1)e^x.
Sa fonction dérivée f '(x) est donnée par :
f '(x) = e^x; f '(x) =(x+2)e^x vrai ; f '(x) = -xe^x ; f '(0) = 0.
On pose u = x+1 et v = e^x ; u' = 1 ; v' = e^x.
u'v+v'u =e^x+(x+1)e^x = (x+2)e^x.

2.Pout tous réels a et b, le nombre e^a /e^-b est égal à :
e^a-b ; e^-a/b ; e^b/e^-a vrai ; e^a-e^b.
e^a /e^-b = e^a x e^b = e^a+b ; e^b/e^-a =e^b x e^a = e^a+b.

3. Soit (u_n) une suite arithmétique telle que : u₃ = 4,5 et u₆ = 3. Alors le premier terme est u₀ et la raison R sont :
u₀=6 et R = -0,5 vrai ; u₀=0,5 et R = 6 ; u₀=6 et R = 0,5 ; u₀=1,5 et R =0,5.
u₄=u₃+R ; u₅=u₄+R =u₃+2R ; u₆=u₅+R =u₃+3R ; R = (u₆-u₃) / 3 = (3-4,5) / 3= -0,5.
u₁=u₀+R ; u₂=u₁+R =u₀+2R ; u₃=u₄+R =u₀+3R ; u₀ = u₃-3R =4,5-3(*-0,5) =6.

4. On considère le programme ci-dessous :
s=0
for i in range(51) :
s = s+i
Quelle est le contenu de la variable s après exécution du programme ?
51 : 1326 ; 1275 vrai ; 2500.
i prend toutes les valeurs entières entre 0 et 50.
s = 0 +1 +2 +...+50.
Somme des 51 premiers termes d'une suite arithmétique de premier terme 0 et de raison 1 :
s = nombre de termes (premier terme + dernier terme) / 2 =51x(0+50) / 2 =1275.

5. La valeur exacte de la somme S = 1 +0,5 +0,5² +...+0,5¹⁵ est :
1,750030518 ; 2-0,5¹⁵ vrai ; 2-0,5¹⁴ ; 1,999969482.
Somme des 16 premiers termes d'une suite géométrique de premier terme 1 et de raison 0,5.
S =(1-0,5¹⁶) / (1-0,5) =2 (1-0,5¹⁶)=2-0,5¹⁵.

Exercice 2.
La courbe ci-dessous représente la puissance en watt en fonction du temps développée par un rameur débutant.
A. Répondre aux questions par lecture graphique.

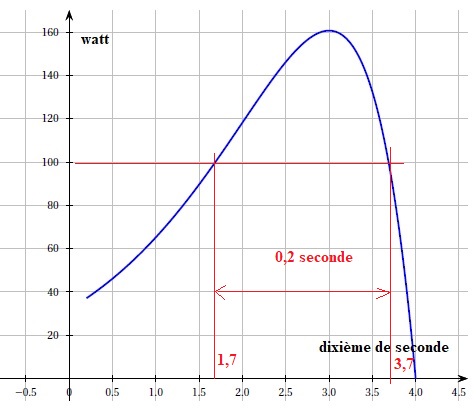
1. Quelle est la puissance maximale ? 160 watts.
2. Pendant combien de temps la puissance reste-t-elle au dessus de 100 W ? 0,2 s.
B. Modélisation par une fonction.
On suppose que la courbe est modélisée par f(x) =(-8x+32)e^x sur [0,2 ; 4].
On admet que f '(x) = (-8x+24)e^x.
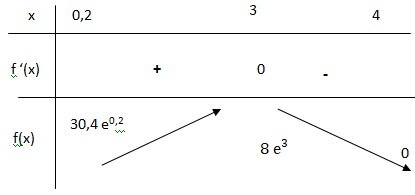
1. Etudier le signe de f '(x) et en déduire les variations de f(x).
e^x>0 ; f '(x) a le signe de -8x+24 ;
f '(x) = 0 si x = 3 ; f '(x) < 0 si x appartient à ]3 ; 4] ; f '(x) >0 si x appartient à [0,3 ; 3[.
2. Déterminer la valeur exacte du maximum.

On suppose que le sportif améliore sa meilleure performance de 5 % tous les mois. Au bout de combien de mois d'entrainement dépassera t-il 200 W ?
Suite géométrique de premier terme 160 et de raison 1,05.
u_n = 160 x1,05ⁿ =200 ; 1,05ⁿ =200 / 160 =1,25 ; n ln(1,05 ) = ln(1,25) ; n = ln(2) / ln(1,25) ~3,1 ( 4 mois).

Exercice 3.
Un magasin commercialise des canapés et des tables de salon. Quand un client se présente, il achète au plus un canapé et au plus une table de salon. Une étude a montré que :
- la probabilité qu'un client achète un canapé est 0,24 ;
- la probabilité qu'un client achète une table de salon quand il a acheté un canapé est 0,25 ;
- la probabilité pour qu'un client achète une table de salon quand il n'a pas acheté de canapé est 0,1.
On choisit un client au hasard et on note :
C l'événement " le client achète une table de salon".
T l'événement " le client achète une table de salon".
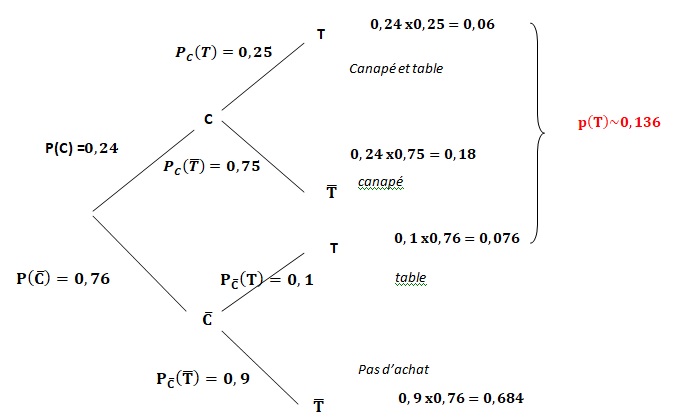
1. Construire l'arbre pondéré représentant la situation.
2. Calculer la probabilité que le client achète un canapé et une table de salon.
3. Montrer que P(T) = 0,136.

4. Le prix moyen d'un canapé est 1000 € et le prix moyen d'une table de salon est 300 €. On note X la variable aléatoire correspondant à la somme payée par le client.
Compléter le tableau donnant la loi de probabilité de X.

x_i	0	300	1000	1300
P(X=x_i)	0,684	0,076	0,18	0,06

Calculer l'espérance de X. Interpréter.
E = 300 x0,076 +1000 x0,18 +1300 x 0,06 =22,8 +180 +78 =280,8.
Un client dépense en moyenne 280,8 €.

Exercice 4.
Le plan est rapporté à un repère orthonormé d'unité 1 cm. On considère la droite D d'équation x+3y-5=0.

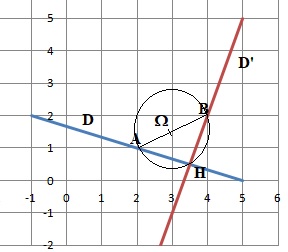
1. Montrer que le point A( 2 ;1 ) appartient à la droite D. Tracer cette droite.
Si A appartient à la droite D, alors x_A +3y_A-5 =0.
2+3-5=0 est vérifié ; A appartient à la droite D.
2. Montrer que la droite D' passant par le point B( 4 ; 2) et perpendiculaire à la droite D, admet pour équation 3x-y-10 =0.
D' est perpendiculaire à D, donc l'équation de D' est : 3x-y+c=0.
B appartient à la droite D' : 3x_B-y_B+c=0.
3*4-2+c=0 ; c = -10.
Equation de D' : 3x-y-10=0.
3. Soit H le projeté orthogonal de B sur la droite D. Déterminer par calcul les coordonnées de H.
H appartient à D : x_H +3y_H-5 =0 soit x_H = -3y_H+5.
H appartient à D' : 3x_H-y_H-10=0.
3(-3y_H+5) -y_H-10=0.
-10 y_H +15-10 = 0 ; y_H =0,5.
x_H =-3*0,5 +5 = 3,5.
H(3,5 ; 0,5)
4. On considère le cercle de diamètre (AB] et on note W son centre.
a. Déterminer une équation du cercle ; préciser son rayon et les coordonnées de son centre.
Diamètre [AB] : AB² =(x_B-x_A)²+(y_B-y_A)² = 2²+1²=5 ; AB = 5^½.
Rayon R = 5^½ / 2 ; R² = 5 /4.
Coordonnées du centre W : (x_A+x_B) / 2 = 3 ; (y_A+y_B) / 2 = 1,5.
Equation du cercle : (x-3)² +(y-1,5)² =5 /4.
b. Le point H appartient-il au cercle ? Justifier.
Si H appartient à ce cercle : (x_H-3)² +(y_H-1,5)² =5 /4.
(0,5)² +(-1)² =1,25 est bien vérifiée, donc H appartient à ce cercle.