Spécialité
Mathématiques, classe de première 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
.
|
|
Exercice 1.
On place un grain de riz sur la première case du jeu d'échec,
puis deux grains sur la case suivante, puis 4 grains sur la
troisième case et anisi de suite, en doublant le nombre de grains de
riz entre une case et la suivante, et ce jusqu'à la 64è case. On note u1 le nombre de grains de riz présents sur la première case, u2 le nombre de grains de riz sur la deuxième case et ainsi de suite.
1. Déterminer u1, u2, u3, u4 et u5.
u1 = 1 ; u2 = 2 ; u3 = 4 ; u4 = 8 ; u5 = 16.
2. Exprimer un+1 en fonction de un.
un+1 = 2 un.
3. En déduire la nature de la suite (un) et en préciser les éléments caractéristiques. Exprimer un en fonction de n.
Suite géométrique de premier terme u1 = 1 et de raison q = 2.
un = 2n-1.
4. Calculer le nombre de grains de riz disposés sur le plateau.
Somme des 64 premiers termes de cette suite : (1-q64) / (1-q) =264-1 = 18 446 744 073 709 551 615.
5.
On veut écrire une fonction en langage Python qui détermine à partir de
quelle case on disposera d'au moins R grains de riz. Compléter
cette fonction.

Exercice 2.
Une urne contient six jetons rouges dont un est marqué "gagnant" et 4
jetons verts dont trois sont marqués " gagnant". On tire au hasard un
jeton dans l'urne et on note les événements suivants :
R : le jeton tiré est rouge.
V : le jeton tiré est vert.
G : le jeton est gagnant.
1. Modéliser la situation à l'aide d'un arbre de probabilité.
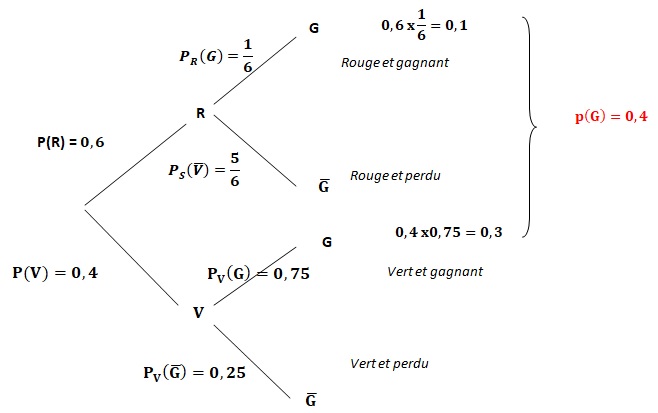
2. Calculer la probabilité de l'événement " le jeton tiré est vert et il est marqué gagnant".
0,4 x0,75 = 0,3.
3. Soit P(G) la probabilité de tirer un jeton gagnant. Montrer que P(G) = 2 /5.
4. Sachant que le jeton tiré est gagnant, calculer la probabilité qu'il soit rouge.
PG(R) = P(G n R) / P(G) = 0,1 / 0,4 = 0,25.
5. On tire
maintenant, toujours au hasard et simultanément, deux jetons dans
l'urne. Calculer la probabilité que les deux jetons soient marqués
gagnant. Expliquer votre démarche.
Il a C210 =10 x9 / 2 = 45 façons de tirer deux jetons.
Il a C24 =4 x3 / 2 = 6 façons de tirer deux jetons gagnants.
Il y a équiprobabilité ; la probabilité de tirer deux jetons gagnants est donc : 6 / 45 = 2 /15.
|
Exercice 3.
On considère la fonction f définie sur R par f(x) = x3+7x2+11x-19. On note C sa courbe représentative.
1. Déterminer l'expression de sa dérivée notée f '(x)..
f '(x) = 3x2+14x+11.
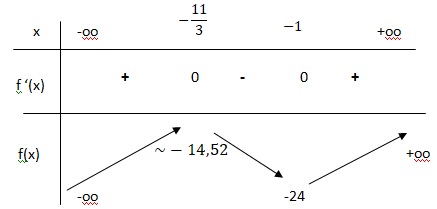
2. Résoudre dans R 3x2+14x+11 >0 et en déduire le tableau de variation de f(x).
3x2+14x+11 =0; discriminant D = 142-4 *3*11 =64 = 82.
Solutions : x = (-14+8) / 6 = -1 et x = (-14-8) / 6 = -11 /3.
a =3 positif, le signe de 3x2+14x+11 est positif en dehors des racines.
]-oo ; -11/3[ union }-1 ; +oo[.
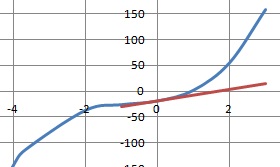
3. Déterminer l'équation réduite de la tangente à la courbe C en x=0.
Coefficient directeur de la tangente f '(0) = 11.
Equation de la tangente y = 11 x+b.
Le point de coordonnées (0 ; -19) appartient à la tangente : -19 =b ; y = 11x -19.
 4. Justifier que 1 est solution de x3+7x2+11x-19 =0. Vérifier que f(x) = (x-1) (x2+8x+19).
4. Justifier que 1 est solution de x3+7x2+11x-19 =0. Vérifier que f(x) = (x-1) (x2+8x+19).
13 +7*12+11*1-19 =1 +7+11-19 = 0.
(x-1) (x2+8x+19) = x3+8x2+19x-x2-8x-19 =x3+7x2+11x-19 =f'x).
5. Etudier le signe de la fonction f et en dresser le tableau de signes sur R.
x2+8x+19 =0 ; discriminant D =82-4*19 = -12. ( pas de solutions réelles).
a = 1 positif, x2+8x+19 >0.
f est du signe de x-1.

Exercice 4.
Dans un repère orthonormé, on considère les points A(3 ; 1), B(-3 ; 3) et C(2 ; 4).
1. Montrer que l'équation x+3y-6=0 est une équation cartésienne de la droite (AB).
A appartient à la droite (AB) : xA+3yA-6 =0 ; 3+3-6= est vérifié.
B appartient à la droite (AB) : xB+3yB-6 =0 ; -3+3*3-6= est vérifié.
L'équation x+3y-6=0 est donc une équation cartésienne de la droite (AB).
2. Déterminer une équation cartésienne de la droite d, perpendiculaire à la droite (AB) et passant par C.
Equation cartésienne de la droite d, perpendiculaire à la droite (AB) : -3x+y+c=0.
C appartient à la droite d : -3xC+yC+c=0 ;
-3*2+4+c = 0 ; c = 2.
Equation cartésienne de la droite d : -3x+y+2=0.
3. En déduire les coordonnées du point K, projeté orthogonal du point C sur la droite (AB).
K appartient à la droite (AB) et à la droite d. K est l'intersection de ces deux droites.
xK+3yK-6=0 et -3xK+yK+2=0.
xK= -3yK+6 ; -3 (-3yK+6 )+yK+2=0.
10yK-16=0 ; yK = 1,6.
Par suite xK =-3*1,6+6=1,2.
K(1,2 ; 1,6).
4. Calculer la distance AB et déterminer les coordonnées du milieu M du segment [AB].
AB2 =(xB-xA)2+(yB-yA)2 = 36+4=40 ; AB = 2 x10½.
xM =(xB+xA) /2 =(3-3) / 2 = 0 ; yM =(yB+yA) /2 =(3+1) / 2 = 2. M( 0 ; 2).
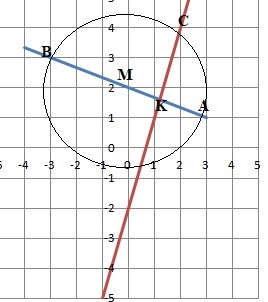
5. En déduire une équation du cercle de diamètre (AB].
M est le centre du cercle et son rayon vaut AB / 2 = 10½.
Equation de ce cercle : (y-2)2 + x2 = 10.
|
|





