Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 63
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1. Une fonction du second degré 𝑓 a pour forme canonique valable pour tout réel 𝑥 :
𝑓(𝑥)=3(𝑥+2)²+5.
Concernant son discriminant :
a) on peut dire qu’il est nul
b) on peut dire qu’il est strictement positif
c) on peut dire qu’il est strictement négatif. Vrai.
d) on ne peut rien dire sur son signe.
Pour tout x réel f(x) > 5. La parabole ne coupe pas l'axe des abscisses ; le discriminant est négatif.
2. Un vecteur directeur de la droite d’équation 2𝑥+3𝑦+5=0 est :
a) 𝑢⃗ (2 ; 3)
b) 𝑢⃗ (−3 ; 2). Vrai.
c) 𝑢⃗ (3 ; 2)
d) 𝑢⃗ (−2 ; 3)
3. Dans un repère orthonormé du plan, on considère les points A(3;−1), B( 4 ;2) et C (1 ;1).
Le produit scalaire suivantest égal à :
a) −4 ; b) 2 ; c) 4 vrai ; d) 8.
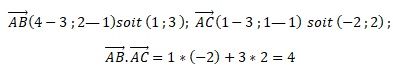
4. Soit 𝑔 la fonction définie sur l’ensemble des nombres réels par 𝑔(𝑥)=(2𝑥+1)e𝑥.
Pour tout réel 𝑥, 𝑔′(𝑥) est égal à :
a) 2e𝑥.
b) 2𝑥e𝑥.
c) (2𝑥+2)e𝑥.
d) (2𝑥+3)e𝑥. Vrai.
On pose u = 2x+1 et v = ex ; u' =2 ; v' = ex ; u'v+v'u=2ex +(2x+1)ex =(2x+3)ex .
5. Pour tout réel 𝑥, sin(𝑥 + 𝜋 ) est égal à :
a) cos 𝑥
b) sin 𝑥
c) −cos 𝑥
d) −sin 𝑥. Vrai.
Sujet 64....
1. On donne ci-contre la courbe représentative 𝐶𝑓 d’une fonction 𝑓.
Cette courbe a une tangente 𝑇 au point 𝐴(−3 ;3).
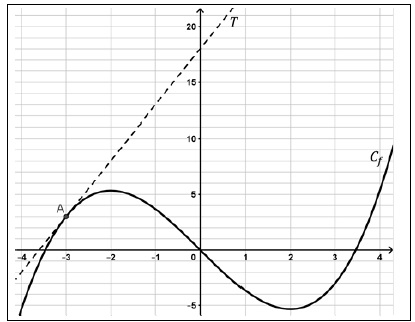
L’équation réduite de cette tangente est :
a) y = 0,2x-3,7 ; b)y=0,2x+18 ; c) y = 5x+18 vrai ; d) y = 5x-3,7.
Coefficient directeur de la tangente : 5.
Equation de la tangente en A : y = 5x+b.
A ( -3; 3) appartient à la tangente : 3 = 5*(-3) +b ; b = 18.
2. On reprend la fonction 𝑓 de la question précédente. La représentation graphique de sa fonction dérivée est :
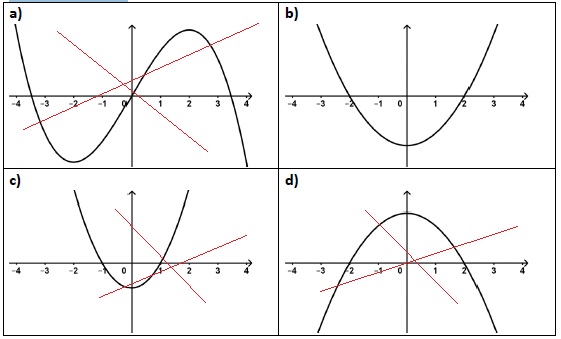 Réponse b. Réponse b.
f est décroissante entre -2 et +2 ; f ' est négative sur [-2 ; 2].
3. L’expression cos(𝑥+𝜋)+sin(𝑥+𝜋/2) est égale à :
a) −2cos(𝑥)
b) 0. Vrai.
c) cos(𝑥)+sin (𝑥)
d) 2cos(𝑥)
cos(𝑥+𝜋) = - cos (x) ; sin(𝑥+𝜋/2) = cos (x).
4. On considère la fonction polynôme du second degré f définie sur ℝ par
𝑓 (𝑥)= −2𝑥2+4𝑥+6.
Cette fonction est strictement positive sur l’intervalle :
a) ]−∞;−1[ ∪ ]3;+∞[
b) ]−1 ;3[ vrai.
c) ]−∞;−3[ ∪ ]1;+∞[
d) ]−3 ;1[.
Solutions de −2𝑥2+4𝑥+6=0 ; D =42-4*6*(-2) =64=82.
Solutions : x1 = (-4 +8) / (2*(-2))= -1 et x1 = (-4 -8) / (2*(-2))= 3. a étant négatif, la parabole présente un maximum.
5. On considère la fonction ℎ définie sur ℝ par ℎ(𝑥)= (2𝑥−1)𝑒𝑥.
La fonction dérivée de la fonction ℎ est définie sur ℝ par :
a) ℎ’(𝑥)= 2𝑒𝑥.
b) ℎ’(𝑥)= (2𝑥+1)𝑒𝑥. Vrai.
c) ℎ’(𝑥)= (2𝑥−1)𝑒𝑥.
d) ℎ’(𝑥)= −𝑒𝑥.
On pose u = (2x-1) et v = 𝑒𝑥 ; u' = 2 ; v' = 𝑒𝑥.
u'v+v'u = 2𝑒𝑥+(2x-1)𝑒𝑥 =(2x+1)𝑒𝑥.
|
|
Exercice 2. ( 5
points) Sujet 63. Durant
l’été, une piscine extérieure perd chaque semaine 4 % de son volume
d’eau par évaporation. On étudie ici un bassin qui contient 80 m3 après son remplissage.
1. Montrer par un calcul que ce bassin contient 76,8 m3 d’eau une semaine après son remplissage.
80 (1-0,04) = 80 *0,96 =76,8 m3.
2. On ne rajoute
pas d’eau dans le bassin et l’eau continue à s’évaporer. On modélise le
volume d’eau contenue dans la piscine par une suite (𝑉𝑛) : pour tout entier naturel 𝑛, on note 𝑉𝑛 la quantité d'eau en m3 contenue dans la piscine 𝑛 semaines après son remplissage. Ainsi 𝑉0=80.
a. Justifier que pour tout entier naturel 𝑛, 𝑉𝑛+1= 0,96 𝑉𝑛 et préciser la nature de la suite (𝑉𝑛) ainsi définie.
La suite est géométrique de raison 1-4/100=0,96 et de premier terme 80.
b. Donner une expression de 𝑉𝑛 en fonction de 𝑛.
Vn = 80 *0,96n.
c. Quelle quantité d’eau contient le bassin au bout de 7 semaines ?
v7 = 80 *0,967 ~60,1 m3.
3. Pour compenser en partie les pertes d’eau provoquées par l’évaporation, on décide de rajouter 2 m3
d’eau chaque semaine dans le bassin. On souhaite déterminer au bout de
combien de semaines, le volume d’eau contenu dans la piscine devient
inférieur à 70 m3.
Compléter la fonction Python suivante afin que l’appel nombreJour(70)
renvoie le nombre de semaines à partir duquel le volume d’eau de la
piscine sera inférieur à 70 m3.
def nombreJour(U) :
N=0
V=80
while V >= 70 :
N=N+1
V=0,96*V
return N
Sujet 64.
Un
globe-trotter a comme objectif de parcourir 2000 km à pied. Il peut
parcourir 50 km en une journée, mais, la fatigue s'accumulant, la
distance qu'il parcourt diminue de 2% chaque nouvelle journée.
On note la distance 𝐷𝑛 la distance parcourue durant le 𝑛-ième jour.
Le premier jour de son périple, il parcourt donc 𝐷1= 50 km.
1. Calculer la distance parcourue le deuxième jour.
D2 = 50 (1-2 /100) = 50 *0,98 =49 km.
2. Quelle est la nature de la suite (𝐷𝑛) ? Donnez ses éléments caractéristiques.
Suite géométrique de raison 0,98 et de premier terme 50.
3. Pour tout entier naturel 𝑛≥1, déterminer l'expression de 𝐷𝑛 en fonction de 𝑛.
Dn = 50 *0,98n.
4. Pour calculer le
nombre de jours qu’il faudra au globe-trotter pour atteindre son
objectif, on a écrit le programme Python suivant :
Compléter les deux lignes incomplètes de ce programme.
def nb_jours:
j=1
u=50
S=50
while S < 2000:
u=0.98*u
S=S+u
j= j+1
return j
5. À l’aide de l’extrait de tableur ci-contre, déterminer quand le globe-trotter aura atteint son objectif.
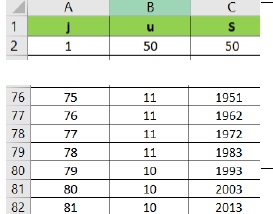
j = 80 jours.
|
|
Exercice 3. ( 5 points).
Sujet 63.
Une petite entreprise de textile commercialise des nappes et des lots de serviettes assorties.
Un client achète au plus une nappe et au plus un lot de serviettes.
En consultant le fichier des ventes de l’entreprise, on constate que :
20% des clients achètent une nappe ;
Parmi les clients ayant acheté une nappe, 70 % ont acheté un lot de serviettes ;
Parmi les clients n’ayant pas acheté de nappe, 10 % ont tout de même acheté un lot de serviettes.
On choisit au hasard un client de cette entreprise.
Pour tout événement 𝐴, on note 𝐴̅ l’événement contraire de 𝐴 et 𝑃(𝐴) la probabilité de l’événement 𝐴.
On note les événements suivants :
𝑁 « le client achète une nappe » ;
𝑆 « le client achète un lot de serviettes ».
1. Reproduire sur la copie et compléter l’arbre pondéré ci-dessous décrivant la situation.
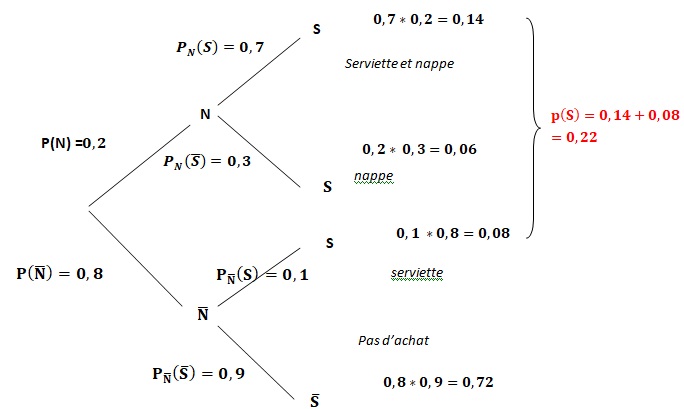
2. Calculer la probabilité que le client achète une nappe et un lot de serviettes.
0,2 *0,7 = 0,14.
3. Montrer que la probabilité de l'événement 𝑆 est égale à 0,22.
0,14 +0,08 = 0,22.
4. Calculer la probabilité que le client achète une nappe sachant qu’il a acheté une serviette.
PS(N) = P(N n S)) / P(S) =0,14 / 0,22 = 14 / 22 = 7 /11.
5. Une nappe est
vendue 45 € et un lot de serviettes 25 €. On appelle 𝐷 la variable
aléatoire donnant la dépense effectuée par un client.
Calculer l'espérance mathématique de 𝐷 et donner une interprétation de ce nombre dans le contexte de l’exercice.
valeurs de D
|
70
|
45
|
25
|
0
|
probabilité
|
0,14
|
0,06
|
0,08
|
0,72
|
Espérance : 70 *0,14 +45 *0,06 +25*0,08 =9,8 +2,7+2 =14,5.
La dépense moyenne d'un client est de 14,5 €.
Sujet 64.
Soit (𝑂,𝑖⃗,𝑗⃗) un repère orthonormé.
On considère le cercle 𝒞 de centre 𝐴(2 ;5) et de rayon 5
1. Montrer qu'une équation du cercle 𝒞 est : 𝑥²+𝑦²−4𝑥−10𝑦=−4.
(x-xA)2 +(y-yA)2= 52 ; (x-2)2 +(y-5)2= 25.
x2-4x+4+y2-10y+25=25 ; x2-4x+y2-10y=-4.
2. Vérifier que le point 𝐵(5;9) appartient à ce cercle.
(5-2)2+(9-5)2=9+16=25.
B appartient donc à ce cercle.
3. Que peut-on dire de la tangente au cercle au point 𝐵 et de la droite (𝐴𝐵) ?
La tangente au cercle en B est perpendiculaire au rayon AB du cercle.
4. Déterminer une équation de la tangente au cercle au point 𝐵.
Coefficient directeur de la droite (AB) : (yB-yA) / (xB-xA) =4 / 3.
Equation réduite de cette droite ; y = 4x / 3 +b.
A(2 ; 5) appartient à cette droite : 5=4*2/3+b ; b = 7 /3.
Equation cartésienne de (AB) : 4x-3y+7=0.
Equation cartésienne de la tangente au cercle en B : 3x+4y+c=0.
B( 5 ; 9) appartient à la tangente : 3*5+4*9+c=0 ; c= -51.
Equation cartésienne de la tangente au cercle en B : 3x+4y-51=0.
5. Calculer les coordonnées des points d’intersection du cercle 𝒞 avec l'axe des ordonnées.
Equation du cercle : x2-4x+y2-10y=-4.
Equation de l'axe des ordonnées : x = 0.
Par suite : y2-10y+4=0.
Solutions de cette équation : discriminant D = (-10)2 -4*4*1 =84= 4 *21 = (2*21½)2.
y1 =(10-2*21½) / 2=5-21½ ; y2 = 5+21½.
|
|
Exercice 4. ( 5 points) Sujet 63. On considère la fonction 𝑃 définie sur l’intervalle [0 ;5] par 𝑃(𝑡)= 100 𝑡 e−𝑡.
1. Calculer 𝑃(0) et 𝑃(5) (on arrondira à l’unité).
P(0) = 0 ; P(5) =500 e-5 ~3.
2. À l’aide d’un
logiciel de calcul formel, on a obtenu une expression de la dérivée de
la fonction 𝑃 : pour tout réel 𝑡 de l’intervalle [0 ;5],
𝑃′(𝑡)=100(1−𝑡)e−𝑡.
a. Utiliser cette expression pour étudier le signe de 𝑃′(𝑡) sur l’intervalle [0 ; 5].
e-t est positif.
Si t < 1, P'(t) >0 ; si t appartient à [1 ; 5], P'(t) < 0. si t = 1, P'(t) =0.
b. En déduire le tableau de variations de la fonction 𝑃 sur l’intervalle [0 ;5].
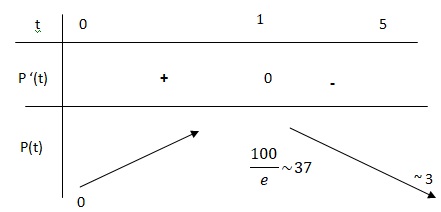
c. Pour quelle valeur de 𝑡 la fonction 𝑃 admet-elle un maximum ? Quelle est la valeur de ce maximum ? (on arrondira à l’unité).
Pour t =1; P(t) admet un maximum proche de 37.
3. Une station
pompe l’eau d’une rivière pour la transformer ensuite en eau potable.
Lors d’un épisode de pollution, il faut interrompre le pompage en
attendant que la vague de pollution soit évacuée par le courant. On
étudie ici un épisode de pollution ayant duré 5 heures environ.
La concentration en polluant, exprimée en milligrammes par litre (mg/L)
est modélisée par la fonction 𝑃 définie précédemment, où 𝑡 est le
temps écoulé depuis le début de l’alerte, exprimé en heures.
On donne ci-dessous la représentation graphique de la fonction 𝑃 dans le plan muni d’un repère orthogonal.
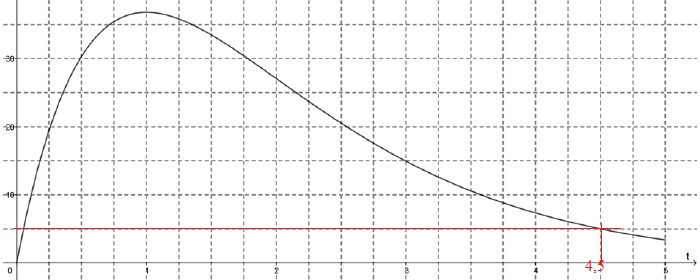
Les normes en vigueur indiquent que ce polluant devient dangereux pour la santé si sa concentration dépasse 5 mg/L.
Lors d’un épisode déclaré de pollution dans la rivière et après arrêt
du pompage, à partir de combien d’heures peut-on considérer que la
pollution ne représente plus de danger pour la santé?
100 𝑡 e−𝑡 < 5 ; t > 4,5 heures.
|
Sujet 64.
Lors
des journées classées « rouges » selon Bison Futé, l’autoroute qui
relie Paris à Limoges en passant par Orléans est surchargée.
Lors de ces journées classées « rouges », on a pu observer le
comportement des automobilistes faisant le trajet de Paris à Limoges en
passant par Orléans.
Pour le trajet de Paris à Orléans, 30 % d’entre eux prennent la route nationale, les autres prennent l’autoroute.
Pour le trajet d’Orléans à Limoges :
- parmi les automobilistes ayant pris la route nationale entre Paris et
Orléans, 40 % prennent la route départementale, les autres prennent
l’autoroute ;
- parmi les automobilistes n’ayant pas pris la route nationale entre
Paris et Orléans, 45 % prennent la route départementale , les autres
prennent l’autoroute.
On choisit un automobiliste au hasard parmi ceux effectuant, en journée
classée rouge, le trajet Paris – Limoges en passant par Orléans.
On note 𝑁 l’événement « l’automobiliste prend la route nationale entre Paris et Orléans »
et 𝐷 l’événement « l’automobiliste prend la route départementale entre Orléans et Limoges ».
Si 𝐴 est un évènement, on note 𝐴̅ l’évènement contraire de 𝐴.
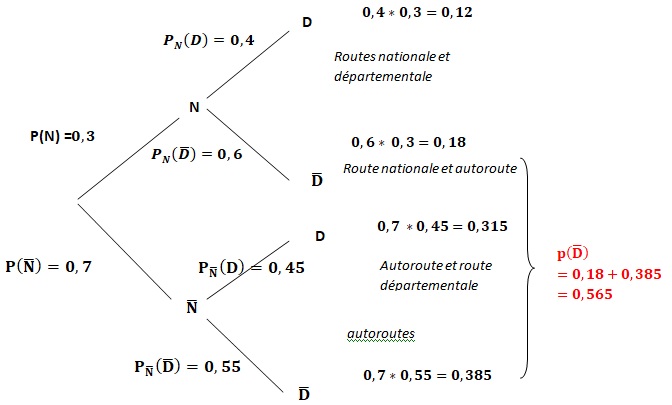
1. Recopier sur la copie et compléter l’arbre ci-dessous.
2. Calculer 𝑃(𝑁̅∩𝐷̅) et interpréter le résultat.
L'automobiliste prend uniquement les autoroutes. 𝑃(𝑁̅∩𝐷̅) =0,7 *0,55 = 0,385.
3. Montrer que la probabilité que l’automobiliste ne choisisse pas la Route Départementale entre Orléans et Limoges est 0,565.
0,18 +0,385 = 0,565.
Lors de ces journées classées « rouges », on donne les temps de parcours suivants :
Paris – Orléans, par autoroute : 3 heures ;
Paris – Orléans, par nationale : 2 heures ;
Orléans – Limoges, par autoroute : 4 heures ;
Orléans – Limoges, par départementale : 3 heures et demie.
4. Recopier et compléter le tableau ci-dessous, qui donne pour chaque trajet, le temps en heure et la probabilité :
| Évènement |
𝑁∩𝐷 |
𝑁 ∩𝐷̅ |
𝑁̅ ∩𝐷 |
𝑁̅ ∩𝐷̅ |
temps ( heures)
|
5,5
|
6
|
6,5
|
7
|
probabilité
|
0,12
|
0,18
|
0,315
|
0,385
|
5. Calculer l’espérance de la variable aléatoire qui donne la durée du trajet en heure et en donner une interprétation.
Espérance : 5,5 *0,12 +6 *0,18 +6,5 *0,315 +7 *0,385 =0,66+1,08+2,0475+2,695=6,4825.
La durée moyenne du trajet est environ 6,5 heures.
|
|