Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
Sujet 49
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1. On considère la droite 𝑑 dont une équation cartésienne dans un repère orthonormé est 2𝑥−3𝑦+4=0.
a. Un vecteur directeur de 𝑑 a pour coordonnées (−6 ; 4). Faux. ( y =2x /3 +4 /3, coefficient directeur 2 / 3 )
b. Un vecteur normal de 𝑑 a pour coordonnées (−12 ; 18). Vrai.
c. Le point 𝐶(−5 ; 2) appartient à la droite 𝑑. Faux.(-5*2-3*2 diffère de zéro).
d. La droite 𝑑 coupe la droite d’équation −𝑥+3𝑦−2=0 au point 𝐹(1 ; 2).
(Les coordonnées de F vérifient : 2-3*2+4 =0 mais ne vérifient pas -1+6-2 =0).
2. Dans un repère orthonormé le cercle 𝒞 a pour équation 𝑥2−2𝑥+𝑦2+𝑦=3 et la droite 𝐷 pour équation 𝑦=1.
a. 𝒞 et 𝐷 n’ont aucun point d’intersection.
b. 𝒞 et 𝐷 ont un seul point d’intersection.
c. 𝒞 et 𝐷 ont deux points d’intersection. Vrai.
d. On ne peut pas savoir combien 𝒞 et 𝐷 ont de points d’intersection.
Les abscisses des points d'intersection vérifient :
x2-2x+1+1=3 ; x2-2x-1=0 ; discriminant D =(-2)2 -4*(-1)=8. Le discriminant étant positif, il y a deux racines réelles.
3. La fonction 𝑓 est la fonction définie sur l’ensemble des réels par 𝑓(𝑥)=cos(2𝑥).
a. 𝑓 est paire. Vrai.
b. 𝑓 est impaire.
c. 𝑓 n’est ni paire ni impaire.
d. 𝑓 a pour période 𝜋 /2.
4. Soit la suite (𝑢𝑛) définie par 𝑢0=1 et pour tout entier naturel 𝑛 par 𝑢𝑛+1=1 / 2(𝑢𝑛+2 / 𝑢𝑛)
On définit en langage Python une fonction « Suite » pour calculer 𝑢𝑛 connaissant 𝑛.

.
Réponse d.
5. L’équation e𝑥=1 :
a. n’a pas de solution.
b. a pour solution le nombre 1.
c. a pour solution le nombre 0.
d. a pour solution le nombre e. Réponse c.
Sujet 50.
1. Pour tout réel 𝑥, l’expression 𝑒𝑥×𝑒𝑥+2 est égale à :
a) 𝑒2𝑥+2
b) 𝑒𝑥²+2
c) 𝑒𝑥 / (𝑥+2)
d) 𝑒𝑥²+2𝑥. Réponse a.
2. Soit
𝑔 une fonction définie et dérivable en 1. Dans un repère du plan, une
équation de la tangente à la courbe de la fonction 𝑔 au point
d’abscisse 1 est :
a) 𝑦=𝑔(1)×(𝑥−1)−𝑔′(1)
b) 𝑦=𝑔′(1)×(𝑥−1)+𝑔(1)
c) 𝑦=𝑔′(1)×(𝑥+1)−𝑔(1)
d) 𝑦=𝑔(1)×(𝑥+1)+𝑔′(1). Réponse b.
Coefficient directeur de la tangente : g'(1).
Equation de la tangente y = g'(1) x+b.
Le point de coordonnées 1 ; g(1) appartient à la tangente : g(1) = g'(1) +b ; b = g(1)-g'(1).
y = g'(1) (x-1) +g(1).
3.
Le plan est muni d’un repère (𝑂 ;𝑖⃗ ,𝑗⃗). On considère la droite
(𝑑) de vecteur directeur de coordonnées (4 ;7) et passant par le point
𝐴(-2 ; 3). Une équation cartésienne de la droite (𝑑) est :
a) −7𝑥+4𝑦−26=0
b) 4𝑥+7𝑦−13=0
c) −7𝑥+4𝑦+26=0
d) 4𝑥−7𝑦+29=0.
Equation de la droite y =7 /4 x+b.
A appartient à la droite : 3 = 7(-2) / 4 +b ; b = 6,5.
y = 7 x / 4 +6,5 soit 4y-7x -26=0. Réponse a.
4. 𝑡 est un réel. On sait que cos(𝑡)= 2 / 3 . Alors cos(𝑡+4π)+cos (−𝑡) est égal à :
a) −4 / 3
b) 0
c) 4 / 3
d) 2 / 3.
cos(𝑡+4π) = cos(𝑡) ; cos (−𝑡) =cos (𝑡) ; cos(𝑡+4π)+cos (−𝑡) = 2 cos(𝑡)= 4 / 3 . Réponse c.
5. On considère, dans un repère du plan, la parabole (P) d’équation :
y=−x2+6x−9. La parabole (P) admet :
a) aucun point d’intersection avec l’axe des abscisses
b) un seul point d’intersection avec l’axe des abscisses
c) deux points d’intersection avec l’axe des abscisses
d) trois points d’intersection avec l’axe des abscisses.
Racines de −x2+6x−9 = 0 ; discriminant D =62-4*(-9)*(-1) =0.
-(x-3)2=0 ; x = 3. Réponse b.
|
|
Exercice 2. ( 5
points) Sujet 49. Dans cet exercice, les résultats seront arrondis au centième.
Un gérant d’un salon de thé achète des boîtes de thé vert chez deux fournisseurs.
Il achète 80 % de ses boîtes chez le fournisseur « Au thé de qualité » et 20 % de ses boîtes chez le fournisseur « Bon thé ».
Des contrôles de qualité montrent que 10 % des boîtes provenant du
fournisseur « Au thé de qualité » présentent des traces de pesticides
et que 20 % de celles provenant du fournisseur « Bon thé » présentent
aussi des traces de pesticides.
On prélève au hasard une boîte du stock du gérant et on considère les événements suivants :
𝐴 : « la boîte provient du fournisseur « Au thé de qualité » » ;
𝐵 : « la boîte provient du fournisseur « Bon thé » » ;
𝑇 : « la boîte présente des traces de pesticides ».
1. Traduire l’énoncé à l’aide d’un arbre pondéré.
2. Quelle est la probabilité que la boîte prélevée provienne du fournisseur A et contienne des traces de pesticide ?
0,8 x0,1 = 0,08.
3. Que représente l’événement 𝐵∩𝑇̅ ? Quelle est la probabilité de cet événement ?
La boîte provient du fournisseur B et ne présente pas de traces de pesticides.
0,2 x0,8 = 0,16.
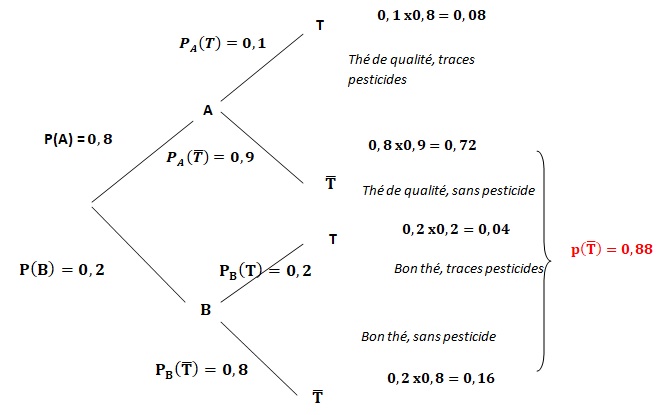
4. Justifier que la probabilité que la boîte ne présente aucune trace de pesticides est égale à 0,88.
0,8 x(1-0,1) +0,2 x(1-0,2) =0,72 +0,16 = 0,88.
5. On constate que
la boîte prélevée présente des traces de pesticides. Quelle est la
probabilité que cette boîte provienne du fournisseur « Bon thé » ?
PT(B)= P(B n T) / P(T)=0,04 /(1-0,88) =4 / 12 = 1 / 3 ~0,33.
Sujet 50.
Dans cet exercice, les distances sont exprimées en mètres.
On considère un rectangle 𝐴𝐵𝐶𝐷 d’aire 49 m2 tel que 𝐷𝐶 = 𝑥 et 𝐵𝐶 = 𝑦.
On admet que les nombres 𝑥 et 𝑦 sont strictement positifs.
On souhaite déterminer les dimensions 𝑥 et 𝑦 pour que le périmètre de ce rectangle soit minimal.
1. a. Montrer que le périmètre, en mètres, du rectangle 𝐴𝐵𝐶𝐷 est égal à 2𝑥+98 / 𝑥.
xy = 49 soit y = 49 /x ; périmètre : 2(x+y) = 2x +98 / x.
b. Calculer ce périmètre pour 𝑥=10.
20+9,8 = 29,8 m.
Soit 𝑓 la fonction définie sur ]0 ;+∞[ par 𝑓(𝑥)=2𝑥+98 / 𝑥.
On admet que 𝑓 est dérivable sur ]0 ; +∞[ et on note 𝑓′ sa fonction dérivée.
2. Montrer que, pour tout 𝑥 > 0,
𝑓′(𝑥)= (2𝑥2−98) / x2.
f '(x) = 2 -98 / x2 = (2𝑥2−98) / x2.
3. Déterminer le tableau de variations de la fonction 𝑓 sur ]0 ; +∞[.
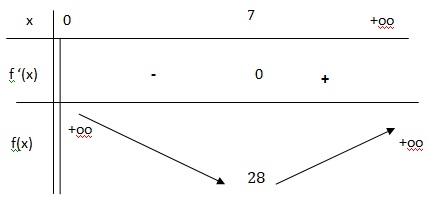
4. En déduire les dimensions du rectangle d’aire 49 m² dont le périmètre est minimal.
x = 7 ; y = 7. C'est un carré.
|
|
Exercice 3. ( 5 points).
Sujet 49.
Un propriétaire propose à un commerçant deux types de contrat pour la location d’un local pendant 3 ans.
1er contrat : un loyer de 200 € pour le premier mois puis une augmentation de 5 € par mois jusqu’à la fin du bail.
2e contrat : un loyer de 200 € pour le premier mois puis une augmentation de 2% par mois jusqu’à la fin du bail.
On modélise ces deux contrats par des suites (𝑢𝑛) et (𝑣𝑛), de sorte que pour tout entier 𝑛≥1, le prix du loyer le 𝑛-ième mois avec le 1er contrat est représenté par 𝑢𝑛 et le prix loyer le 𝑛-ième mois avec le 2e contrat est représenté par 𝑣𝑛.
On a ainsi 𝑢1=𝑣1=200.
1. Calculer, pour chacun des deux contrats, le loyer du deuxième mois puis le loyer du troisième mois.
u2 =205 € ; u3 = 210 €.
v2 =200 x1,02 =204 € ; v3 =204 x1,02 =208,08 € .
2. Le commerçant a écrit un programme en langage Python qui lui permet de déterminer 𝑢𝑛 et 𝑣𝑛 pour une valeur donnée de 𝑛.
1. u=200
2. v=200
3. n=int(input("Saisir une valeur de n :"))
4. for i in range(1,n):
5. u= u+5
6. v=v*1,02
7. print("Pour n =",n,"on a","u =",u," et v =",v)
a) Recopier et compléter les lignes 5 et 6 de ce programme.
b) Quels nombres obtiendra-t-on avec 𝑛=4 ?
u4 = 200 +4 x5 = 220 €.
v4 = 200 x1,024 ~ 216,49 €.
3. Déterminer, pour tout entier 𝑛≥1, l’expression de 𝑢𝑛 et de 𝑣𝑛 en fonction de 𝑛.
un = 200 +5(n-1).
vn = 200 x1,02n-1.
4. Quel contrat coûtera le moins cher au total pour l’ensemble d’un bail de 3 ans ?
Somme des 36 premiers termes de chaque suite :
u1 = 200 ; u36 = 200+35x5 =375 ; 18x(200+375)=10 350 €.
200 x(1-1,0236) /(1-1,02) =10 398,87 €. Le contrat n°1 est le moins cher.
Sujet 50.
Un constructeur de véhicules fabrique deux types d’automobiles : « Citadine » ou « Routière ».
Pour ces véhicules, ce constructeur propose deux finitions :
– « Sport » au tarif de 2500 euros par véhicule,
– « Luxe » au tarif de 4000 euros par véhicule.
En consultant le carnet de commandes de ce constructeur, on recueille les indications suivantes :
80% des clients ont commandé une automobile « Citadine ». Les autres clients ont commandé une automobile « Routière ».
Parmi les clients possédant une automobile « Citadine », 70% ont pris la finition « Sport ».
Parmi les clients possédant une automobile « Routière », 60% ont pris la finition « Luxe ».
On choisit un client au hasard et on considère les évènements suivants :
𝐶 : « Le client a commandé une automobile « Citadine » »,
𝐿 : « Le client a choisi la finition « Luxe » ».
D’une manière générale, on note 𝐴̅ l’évènement contraire d’un évènement 𝐴.
On note 𝑋 la variable aléatoire qui donne le montant en euros de la finition choisie par un client.
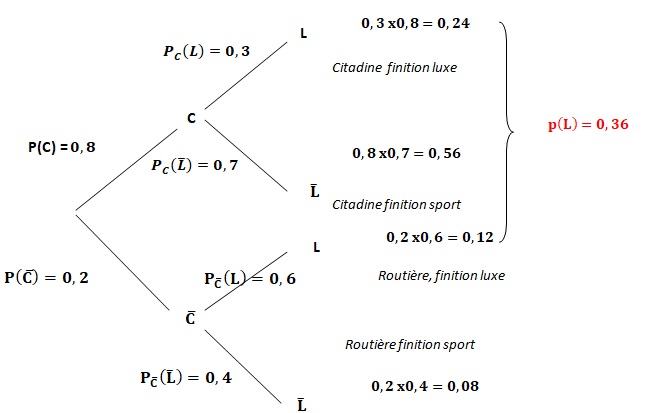
1. Construire l’arbre pondéré de probabilité traduisant les données de l’exercice.
2. Calculer la
probabilité que le client ait commandé une automobile « Citadine » et
ait choisi la finition « Luxe », c’est-à-dire calculer 𝑃(𝐶∩𝐿) .
0,3 x0,8 = 0,24.
3. Justifier que 𝑃(𝐿)=0,36.
4. La variable aléatoire X ne prend que deux valeurs 𝑎 et 𝑏.
a. Déterminer les probabilités 𝑃(𝑋=𝑎) et 𝑃(𝑋=𝑏).
Version luxe : P(L ) = 0,36 ; a = 4000 ;
Version sport : P(non L) = 1-0,36 = 0,64 ; b = 2500.
b. Déterminer l’espérance de 𝑋.
E =4000 x 0,36 +2500 x 0,64 =1 440 + 1600 =3040 €.
|
|
Exercice 4. ( 5 points) Sujet 49 On considère la fonction 𝑓 définie et dérivable sur 𝐑 par 𝑓(𝑥)=(𝑎𝑥+𝑏)e−0,1𝑥 où 𝑎 et 𝑏 sont des réels fixés.
La courbe représentative 𝒞𝑓 de la fonction 𝑓 est donnée ci-dessous, dans un repère orthogonal.
On a également représenté la tangente 𝑇 à 𝒞𝑓 au point 𝐴(0 ;5).
On admet que cette tangente 𝑇 passe par le point 𝐵(4 ;19).
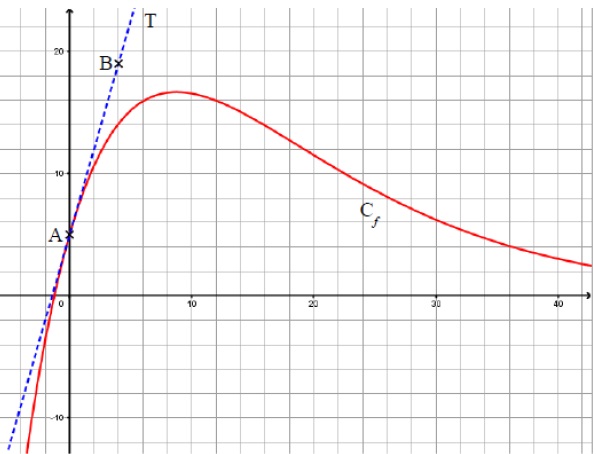
1. En exprimant 𝑓(0), déterminer la valeur de 𝑏.
f(0) = b =xA=5.
2. a) À l’aide des coordonnées des points 𝐴 et 𝐵, déterminer une équation de la droite 𝑇.
Coefficient directeur de T : (yB-yA) /(xB-xA) =(19-5) / 4 =3,5.
A appartient à T : 5 =b ; équation de T : y = 3,5x+5.
b) Exprimer, pour tout réel 𝑥, 𝑓′(𝑥) en fonction de 𝑥 et de 𝑎 et en déduire que pour tout réel 𝑥, 𝑓(𝑥)=(4𝑥+5)e−0,1𝑥.
On pose u = ax+5 et v = e-0,1x ; u' =a ; v' = -0,1e-0,1x ; u'v + v'u = ae-0,1x -0,1(ax+5)e-0,1x =(-0,1ax+a-0,5)e-0,1x .
f '(0) = 3,5 =a-0,5 ; a =4.
3. On souhaite déterminer le maximum de la fonction 𝑓 sur 𝐑.
a) Montrer que pour tout 𝑥∈𝐑, 𝑓′(𝑥)=(−0,4𝑥+3,5)e−0,1𝑥.
f '(x) = (-0,4x+4-0,5)e-0,1x =(−0,4𝑥+3,5)e−0,1𝑥.
b) Déterminer les variations de 𝑓 sur 𝐑 et en déduire le maximum de 𝑓 sur 𝐑.
e−0,1𝑥 >0, le signe de f '(x) est celui de −0,4𝑥+3,5.
Si x < 3,5 /0,4 soit x < 8,75, f '(x) >0 et f(x) croissante.
Si x > 8,75, f '(x) < 0 et f(x) décroissante.
Si x = 8,75, f '(x) =0 et f(x) présente un maximum.
f(8,75) =(4 *8,75+5)e-0,875 =40 e-0,875 ~16,7.
|
Sujet 50.
Fanny
est inscrite dans un club d’athlétisme. Elle pratique le penta bond (le
penta bond est un enchaînement de cinq bonds après une course d’élan).
La première semaine d’entraînement, Fanny réalise un saut de 8 m.
Chaque semaine, la longueur de son saut augmente de 0,1 m.
Pour 𝑛 entier naturel non nul, on note 𝑠𝑛 la longueur, en mètres, de son saut la 𝑛-ième semaine d’entraînement.
Puisque lors de la première semaine d’entraînement, Fanny réalise un saut de 8 m, on a
𝑠1=8.
1. Pour 𝑛≥2, on considère la fonction Python suivante.
def saut(n)
s=8
for k in range(2,n+1) :
s = s+0,1
return s
a. Quelle valeur 𝑠 est-elle renvoyée par la commande saut(4) ?
s = 8 +0,4 = 8,4 m.
b. Interpréter cette valeur dans le contexte de l’exercice.
A la fin de la quatrième semaine, elle saute 8,4 m.
2. Exprimer avec justification 𝑠𝑛 en fonction de 𝑛 pour 𝑛 entier naturel non nul.
sn = 8 +0,1(n-1).
3. Pour être qualifiée à une compétition, Fanny doit faire un saut d’au moins 12 mètres.
a. À partir de quelle semaine, Fanny réalisera-t-elle un tel saut ?
b. Justifier votre réponse.
8+0,1(n-1) = 12 ; 0,1(n-1) = 4 ; n-1 = 4 /0,1 = 40 ; n = 41.
|
|