Mathématiques, QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.


. .

Sujet 37
Exercice 1. ( 5 points ).
QCM ( aucune justification n'est demandée).
1.Soit x un nombre réel. On peut affirmer que :
a) cos(x) = sin⁡(x)  ; b) cos(p − x) = cos(𝜋 + x)
c) sin(𝜋 + x) = sin⁡(𝜋 − x) ; d) cos (𝜋/2+ 𝑥) = cos (𝜋/2− 𝑥). Réponse b.

 2. Les solutions dans l’intervalle [0; 2p[ de l’équation sin(x) = − 3½ / 2 sont :
a) 4 p / 3 et 5 p / 3 ;
b) 2 p / 3 et 4 p / 3 ;
c)  p / 3 et  5 p / 3 ;
d) −2 p / 3 et - p / 3 ;
sin (-p/3) = − 3½ / 2. x = -p/3 ou 5 p /3 et x = p-(-p/3 )= 4 p /3. Réponse a.

3. On considère ABCD un carré direct dans lequel on construit un triangle ABE équilatéral direct.
On note AB=a.
On peut alors affirmer que : 

Réponse c.

4.  Soient deux vecteurs. On peut affirmer que :


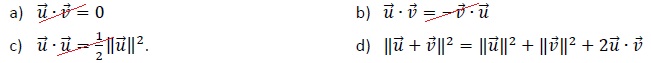
Réponse d.
5. Soit n un entier naturel.
On cherche à exprimer en fonction de n la somme suivante :
S=1−2+4−8+16−32+⋯+(−2)n.
On peut affirmer que :
a) S=1+(−2)n / 2×(n+1)
b) S est la somme des termes d’une suite arithmétique de raison (−2)
c) S=[1−(−2)n] / (1−2)
d) S=1/3[1−(−2)n+1].
Il s'agit d'une suite géométrique de raison -2 et de premier terme 1.
S = 1 *[1-(-2)n+1] / (1-(-2)).
 Réponse d.

Sujet 38.
1. L’inéquation −3(x − 2)(x + 1) > 0 admet pour ensemble des solutions :
a) [-1 ;2] ; b) ] − ∞; −1[∪ [2; +∞[ ; c) ] − 1 ; 2[ ; d) ] − ∞; −1[∪]2; +∞[.
-3x2+3x+6 >0 ; a est négatif, la parabole présente un maximum et -3x2+3x+6 >0 sur ]-1 ; 2[.  Réponse c.

 2. Soit x un nombre réel. Le réel cos(x + 3p) est égal à :
a) cos⁡(x) ; b) −cos⁡(x) ; c) sin⁡(x) ; d) −sin⁡(x). Réponse b.
cos(x + 3p)= cos(x +p+ 2p)= cos ( x+p)= - cos (x).

3. Dans un repère orthonormé, on considère la droite d passant par le point A(1; 2) et dont un vecteur normal est le vecteur⁡ de coordonnées ( 2 ; -3). Une équation de la droite d est :
a) 2x + 3y − 8 =0  ; b) x + 2y + 4 = 0 ; c) 2x − 3y − 4 = 0  ; d) y =2 /3 x + 4 /3.
Réponse d.
Equation cartésienne de la droite d : 2x-3y +c = 0.
A appartient à la droite d : 2xA-3yA + c=0 ; 2-3*2+c=0 ; c = 4.
2x-3y+4=0 ou y = 2x / 3+ 4 /3.
4. On considère la fonction f définie sur [0; +∞[ par f(x) = x2 / (x+1).
On note C sa courbe représentative sur [0; +∞[.
Le coefficient directeur de la tangente à C au point d’abscisse 1 est :
a) 0,5 ; b) 0,75 ; c) 1,5 ; d) 2.
 Réponse b.
On pose u = x2 et v =x+1 ; u' = 2x ; v' = 1 ; f '(x) =(u'v-v'u) / v2 = [2x (x+1) -x2] /(x+1)2 =(x2+2x) / (x+1)2.
f '(1) =3 /4 = 0,75.
5. L’ensemble des points M(x; y) dont les coordonnées vérifient l’équation x2 − 2x + y2 + 4y = 4 est :
a) une droite
b) le cercle de centre A(1; −2) et de rayon 3
c) le cercle de centre B(−1; 2) et de rayon 9
d) l’ensemble vide.
x2 − 2x +1-1+ y2 + 4y +4-4= 4 ; (x-1)2 +(y+2)2 =9.
Réponse b.

Exercice 2. ( 5 points)  Sujet 37.

Un magasin effectue des promotions avant sa liquidation définitive, chaque semaine les prix des articles sont diminués de 10⁡% par rapport à la semaine précédente.
Un manteau coûte 200⁡€ ⁡avant le début de la liquidation, on pose u0=200 et on note un son prix lors de la n-ième semaine de liquidation.
1. Calculer les termes u1 et u2 de la suite (un).
u1 = u0 x(1-10 /100) = 200 x 0,9 =180.
u2 = 0,9 x u1 = 0,9 x180=162.
2. Montrer que la suite (un) est une suite géométrique de premier terme u0=200 dont on précisera la raison et exprimer le terme général de la suite (un) en fonction de n.
un+1 / un = 0,9 , suite géométrique de raison 0,9 et de premier terme u0 = 200.
un = 200 x0,9n.
3. La liquidation dure 12 semaines, déterminer le prix du manteau à la fin de la liquidation s’il est toujours en vente. On donnera le résultat arrondi au centime.
u12=200 x 0,912 =56,49 €.
4. On considère la fonction suivante, écrite en langage Python :
def seuil(x) :
u = 200
n = 0
while u > x :
u =0,9*u
n =n+1
return n
Recopier et compléter sur la copie la fonction afin qu’elle renvoie le nombre de semaines nécessaires pour que le terme général de la suite (un) soit inférieur au nombre réel x.
5. Une personne décide d’acheter le manteau dès que son prix sera inférieur à 100 ⁡€. Combien de semaines devra-t-elle attendre ?
u7=200 x0,97 =95,66. u6=200 x0,96 =106,29.
Elle doit attendre 7 semaines.

Sujet 38.
Un snack propose deux types de plats : des sandwichs et des pizzas.
Le snack propose également plusieurs desserts.
La gérante constate que 80% des clients qui achètent un plat choisissent un sandwich et que parmi ceux-ci seulement 30% prennent également un dessert.
Elle constate aussi que 45 % des clients qui ont choisi une pizza comme plat ne prennent pas de dessert.
On choisit au hasard un client ayant acheté un plat dans ce snack.
On considère les évènements suivants :
S : « Le client interrogé a choisi un sandwich ».
T : « Le client interrogé a choisi un dessert ».
1. Sans justifier, recopier puis compléter l’arbre pondéré suivant :

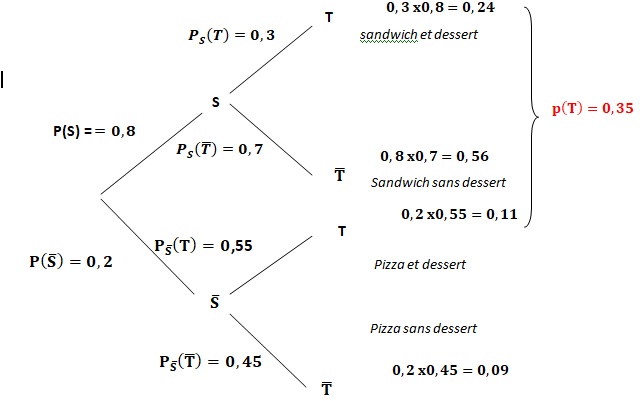
2. Calculer la probabilité que le client ait choisi un sandwich et un dessert. 0,3 x0,8 = 0,24.
3. Démontrer que P(T) = 0,35.
4. Sachant que le client a acheté un dessert, quelle est la probabilité, arrondie à 0, 01 près, qu’il ait acheté une pizza ?
PT(non S) =P(T n non S) / P(T) =0,11 / 0,35 ~0,31.
5. Les événements S et T sont-ils indépendants ?
P(S) = 0,8 ; P(T) =0,35 ; P(S) x P(T) = 0,8 x 0,35 = 0,28 diffère de P(S n T).
Les événements S et T ne sont pas indépendants.

Exercice 3. ( 5 points).
Sujet 37.
Afin d’établir les liens entre le surpoids et l’alimentation, on interroge les enfants des écoles primaires d’une ville.
L’enquête révèle que 60⁡% des enfants boivent 1 boisson sucrée ou plus par jour.
Parmi les enfants buvant 1 boisson sucrée ou plus par jour, un enfant sur 8 est en surpoids, contre seulement 8⁡% pour les enfants buvant moins d’une boisson sucrée par jour.
On choisit un enfant au hasard parmi les enfants des écoles primaires de la ville et on considère les événements suivants :
B : « l’enfant boit 1 boisson sucrée ou plus par jour »,
S : « l’enfant est en surpoids ».
1. Justifier que PB(S)=0,125.
Parmi les enfants buvant 1 boisson sucrée ou plus par jour, un enfant sur 8 est en surpoids.
1 / 8 = 0,125.
2. Représenter la situation par un arbre pondéré.


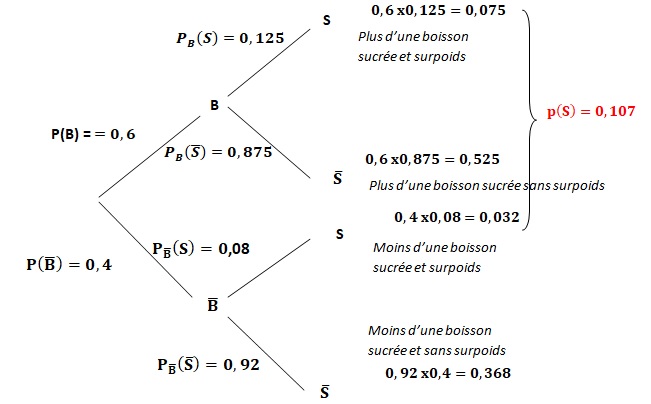
3. Calculer P(B∩S).
0,6 x 0,125 = 0,075.
4. Déterminer la probabilité que l’enfant soit en surpoids.
5. On a choisi un enfant en surpoids. Quelle est la probabilité qu’il boive 1 boisson sucrée ou plus par jour ? On arrondira le résultat au millième.
PS(B) = P(B∩S) / P(S) = 0,075 / 0,107 =0,701.

Sujet 38.

Désirant participer à une course de 150 km, un cycliste prévoit l’entraînement suivant :
 parcourir 30 km en première semaine ;
 chaque semaine qui suit, augmenter la distance parcourue de 9% par rapport à celle parcourue la semaine précédente.
On modélise la distance parcourue chaque semaine à l’entrainement par la suite (dn) où dn représente la distance en km parcourue pendant la n-ième semaine d’entraînement.
On a ainsi d1 = 30.
1. Prouver que d3 = 35,643.
d2 = d1(1+9 /100) = 1,09 d1 =1,09 x 30 =32,7 ;  d3 = 1,09 d2 =1,09 x32,7 =35,643.
2. Quelle est la nature de la suite (dn)⁡?⁡ Justifier.
dn+1 / dn = 1,09 ; suite géométrique de raison 1,09 et de premier terme d1=30.
3. En déduire l’expression de dn en fonction de n.
dn = d1 x1,09n-1 = 30 x1,09n-1.
4. On considère la fonction définie de la façon suivante en langage Python.
def distance (k) :
d =30
n=1
while d <=k:
d=d*1,09
n=n+1
return n
Quelle information est obtenue par le calcul de distance(150) ?
La distance parcourue est égale à 150 km au bout de n =20 semaines.
d20 = 30 x1,0919=154 km.
5. Calculer la distance totale parcourue par le cycliste pendant les 20 premières semaines d’entraînement.
d1(1-1,0920) / (1-1,09) =1534,8 km.



Exercice 4. ( 5 points) Sujet 37

On considère la fonction f définie sur l’intervalle [−4 ; 4] par f(x)=x3+3x2−9x−20. On admet que la fonction f est dérivable sur l’intervalle [−4 ; 4] et on note f ′ sa fonction dérivée.
La courbe représentative de la fonction f, notée C, est tracée dans le repère ci-dessous.
La droite T tracée dans le repère est la tangente à la courbe C au point d’abscisse 0.

1. Déterminer graphiquement les extrema de la fonction f.
2. Déterminer l’expression de f ′(x) sur [−4;4].
f '(x) = 3x2+6x-9.
3. Étudier le signe de 3x2+6x−9 en fonction de ⁡x sur [−4;4].
Solutions de 3x2+6x−9 =0 ; discriminant D = 62-4*3*(-9) =144 = 122.
x1 =(-6+12) / 6 = 1 ; x2 = (-6-12) / 6 = -3.
a étant positif, 3x2+6x-9 >0 sur [-4 ; -3[ union ]1 ; 4] et f(x) est strictement croissante.
3x2+6x-9 <0 sur ]-3 ; 1[  et f(x) est strictement décroissante.
f '(x) = 0 pour x = -3 ( f(x) présente un maximum) et pour x = 1 ( f(x) présente un minimum).
4. En déduire le tableau de variations de f ⁡sur [−4 ; 4] et retrouver les résultats de la question 1.

5. Déterminer l’équation réduite de la droite T, tangente à la courbe C au point d’abscisse 0.
Coefficient directeur de T : f  '(0) = -9.
Equation de T : y = -9x +b.
Le point de coordonnées (0 ; -20) appartient à T : -20 = -9*0 +b ; b = -20.
y = -9x-20.
Sujet 38.
1. Soit f la fonction définie sur l’intervalle [0; 2] par f(x) = 8x − 2x3.
a. Montrer que pour tout réel x de [0; 2], f ′(x) a le même signe que 4 − 3x2.
f '(x) =8-6x2= 2(4-3x2).
b. Étudier les variations de la fonction f ⁡sur [0 ; 2].
Solution  de 4-3x2 = 0 appartenant à [0 ; 2 ] : x = 2 / 3½.

2. Dans un repère orthonormal, on considère la parabole p d’équation y = x2 et la droite d d’équation y = 4.
On considère le rectangle MSFE tel que :
 M un point de p dont l’abscisse x est un réel de ]0 ; 2[.
 S est le symétrique de M par rapport à l’axe des ordonnées.
 E et F sont respectivement les projetés orthogonaux de M et S sur la droite d.

a. Lorsque l’abscisse x du point M varie dans ]0 ; 2[,⁡l’aire du rectangle MSFE est-elle constante ?
b. Montrer que l’aire du rectangle MSFE en fonction de l’abscisse x de M est 8x − 2x3.
Aire du rectangle :  MS * ME = 2x *(4-x2) =8x-2x3.
L'aire du rectangle n'est pas constante si x varie.
c. Montrer que l’aire maximale du rectangle MSFE est 32 / (3*3½).
f(x) présente un maximum égal à 32 / (3*3½) pour x =2 / 3½.
.


  

menu