Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 31
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1.On considère une fonction f définie sur R par :
f(x) = ax2 + bx + c, où a, b et c sont des nombres réels. Δ désigne la quantité b2 − 4ac .
Parmi les affirmations suivantes, laquelle est cohérente avec la représentation graphique de cette fonction ?
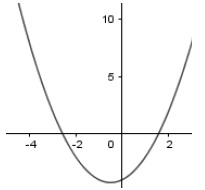
a) a > 0 et Δ > 0 vrai ; b) a < 0 et Δ < 0 ; c) a > 0 et Δ < 0 ; d) a < 0 et Δ > 0.
La courbe admet un minimum, donc a > 0. La courbe coupe l'axe des abscisses en deux points, donc D >0.
2.
Lors d’un jeu, on mise 1 euro et on tire une carte au hasard parmi 30
cartes numérotées de 1 à 30. On gagne 3 euros si le nombre porté sur la
carte est premier, sinon, on ne gagne rien. On détermine le gain
algébrique en déduisant le montant de la mise de celui du gain.
On note X la variable aléatoire qui prend pour valeur le gain algébrique. Que vaut l’espérance E(X) de la variable aléatoire X ?
a) 1 / 3 ; b) 1 / 10 ; c) 0 ; d) 2 /3.
10 nombres premiers : 2, 3 ; 5 ; 7 ; 11 ; 13 ; 17 ; 19 ; 23 ; 29.
valeurs xi ( €)
|
-1
|
2
|
P(X = xi)
|
20 / 30 = 2 / 3
|
10 / 30 =1 /3
|
E(X) = -1 *(2 / 3) + 2*1 /3 = 0. Réponse c.
3. Quelle est la valeur exacte de e6×e3 / e2 ?
a) e11; b) e9 ; c) e7 ; d) e−7.
e6+3-2 = e7. Réponse c.
4. On considère la suite arithmétique (un) de raison −5 et telle que u1 = 2. Quelle est, pour tout entier naturel n, l’expression du terme général un de cette suite ?
a) un = 2 − 5n ; b) un = −5 + 2n ; c) un = 7 − 5n ; d) un = 2 × (−5)n.
un = u1 +(-5)*(n-1) =2-5n +5 =7-5n. Réponse c.
5. Les
équations cartésiennes ci-dessous sont celles de droites données du
plan. Le vecteur de coordonnées (-1 ; 2) est un vecteur normal à l’une
de ces droites. Quelle est l’équation de cette droite ?
a) 2x + y + 5 = 0; b) x + 2y + 3 = 0 ; c) −x + 0,5y + 2 = 0 ; d)−4x + 8y = 0.
Equation de cette droite -x +2y +c=0 avec c une constante ;
-4x +8y =0 soit -x +2y +0 = 0 convient. Réponse d.
Sujet 32.
1. Soit la fonction P définie sur R par P(x) = (x2 + x + 1)(x − 1).
L’équation P(x) = 0 :
a. n’a pas de solution sur R
b. a une unique solution sur R
c. a exactement deux solutions sur R
d. a exactement trois solutions sur R. Réponse b.
x-1 = 0 soit x = 1.
x2 + x + 1 = 0 ; le discriminant D =12-4 = -3 étant négatif il n'y a pas de solutions réelles.
2. Soit la fonction f définie sur R par f(x) = (7x − 23)(ex + 1).
L’équation f(x) = 0 :
a. admet x = 1 comme solution ; b. admet deux solutions sur R
c. admet x = 23 / 7 comme solution ; d. admet x = 0 comme solution.. Réponse c.
ex étant toujours positif, ex+1 ne s'annule pas. f(x) =0 est équivalent à 7x-23 = 0 soit x = 23 /7.
3. Dans le plan rapporté à un repère orthonormé, le cercle de centre A(−4 ; 2) et de rayon r = racine carrée(2) a pour équation :
a. (x + 4)2 + (y − 2)2 = √2= 2½.
b. (x − 4)2 + (y − 2)2 = 4
c. (x + 4)2 + (y − 2)2 = 2
d. (x − 4)2 + (y + 2)2 = 2. Réponse c.
4.
Dans le plan rapporté à un repère orthonormé, on considère les vecteurs
de coordonnées (m + 1 ; −1) et (m ; 2) où m est un réel.
Une valeur de m pour laquelle les vecteurs sont orthogonaux est :
a. m = -2 / 3 ; b. m = −2 ; c. m = 2 ; d. m = −1. Réponse b.
(m+1) m +2*(-1) =0 ; m2+m-2 = 0.
Discriminant D = 12-4*(-2) =9 = 32.
Racines : m = (-1 ±3) / 2 soit -2 et 1.
5.
Dans le plan rapporté à un repère orthonormé, une équation cartésienne
de la droite D passant par le point A(−2 ; 5) et admettant le vecteur
normal de coordonnées (−1 ; 3) est :
a. −x + 3y + 7 = 0 ; b. x − 3y + 17 = 0 ; c. −3x − y − 1 = 0 ; d. −x − 3y + 13 = 0.
Equation de la droite -x+3y+c=0.
Les coordonnées de A vérifient l'équation de la droite : -(-2)+3*5+c = 0 soit c = -17.
Equation : -x+3y-17 = 0 ou x-3y+17=0.
Réponse b.
|
|
Exercice 2. ( 5
points) Sujet 31. Soit f la fonction définie sur R par : f(x)=(5−2x)ex.
On note C la courbe représentative de f. Sur la figure ci-dessous, on a
tracé la courbe C dans un repère orthogonal où les unités ont été
effacées.
A est le point d’intersection de C avec l’axe des ordonnées et B le point d’intersection de C avec l’axe des abscisses.
D est le point de C dont l’ordonnée est le maximum de la fonction f sur R.
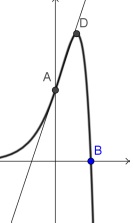
1. Calculer les coordonnées des points A et B.
En A, x = 0 ; f(0)=5e0 = 5.
En B : f(x) = 0 = (5-2x)ex soit x = 2,5.
2. Soit f ′ la fonction dérivée de f sur R. Montrer que, pour tout réel x, f′(x)=(3−2x)ex.
On pose u = (5-2x) et v = ex ; u' = -2 ; v' = ex ; u'v+v'u = -2ex +(5-2x)ex =(3−2x)ex.
3. Étudier le sens de variation de la fonction f.
ex est toujours positif.
f '(x) > 0 si x < 1n5 et f(x) est strictement croissante.
f '(x) < 0 si x > 1,5 et f(x) est strictement décroissante.
f '(x) = 0 pour x = 1,5 et f(x) présente un maximum.
4. En déduire que le point D admet comme coordonnées (1,5 ; 2e1,5).
f(1,5) = (5-3)e1,5 = 2 e1,5.
5. Déterminer une
équation de la tangente à la courbe C au point A, puis vérifier, à
l’aide de l’équation obtenue, que le point D n’appartient pas à cette
tangente.
Coefficient directeur de la tangente en A : f '(0) =3e0 = 3.
Equation de cette tangente : y = 3 x+b.
A (0 ; 5) appartient à cette droite : 5 = b ; y = 3x+5.
Si D appartient à cette droite : 3 xD +5 =3*1,5 +5 = 9,5 différe de yD =2e1,5 ; donc D n'appartient pas à cette droite.
Sujet 32.
Une
entreprise vend des téléviseurs. Une étude a montré que ces téléviseurs
peuvent rencontrer deux types de défauts : un défaut sur la dalle, un
défaut sur le condensateur.
L’étude indique que :
3% des téléviseurs présentent un défaut sur la dalle et que parmi ceux-ci, 2% ont également un défaut sur le condensateur.
5% des téléviseurs ont un défaut sur le condensateur.
On choisit un téléviseur au hasard et on considère les événements suivants :
D : « le téléviseur a un défaut sur la dalle » ;
C : « le téléviseur a un défaut sur le condensateur ».
Les résultats seront approchés si nécessaire à 10-4 près.
1. Justifier que P(D) = 0,03 puis donner PD(C).
3 % = 3 /100 = 0,03 ; probabilité qu'un téléviseur est un défaut de dalle : P(D) = 0,03.
PD(C) = P(D n C) / P(D) =0,03 x0,02 / 0,03 = 0,02.
2. Recopier l’arbre ci-dessous et compléter uniquement les pointillés par les probabilités associées :
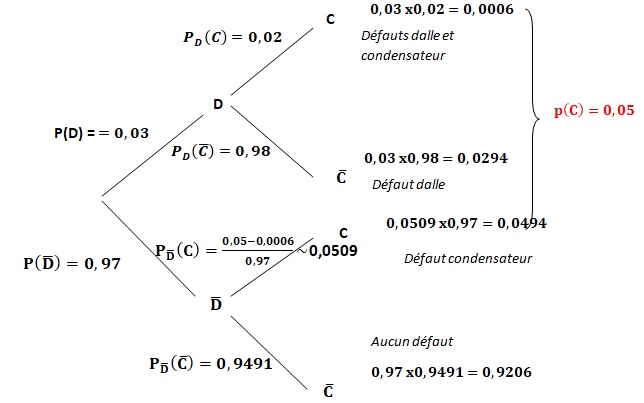
3. Calculer la probabilité P(D ∩ C) de l’événement D ∩ C.
P(D ∩ C) =0,0006.
4. Le téléviseur choisi a un défaut sur le condensateur. Quelle est alors la probabilité qu’il ait un défaut sur la dalle ?
PC(D) =P(D ∩ C) / P(C) =0,0006 / 0,05 =0,012.
5. Montrer que la
probabilité que le téléviseur choisi ait un défaut sur le condensateur
et n’ait pas de défaut sur la dalle est égale à 0,0494.
|
|
Exercice 3. ( 5 points).
Sujet 31.
On injecte dans le sang d’un malade 2 cm3 d’un médicament. On admet que le processus d’élimination du médicament peut être modélisé par une suite (un), dont le terme général un représente le volume en cm3
de médicament présent dans le sang au bout de n heures, n étant un
entier naturel. Dans ce modèle, on considère que le volume de
médicament contenu dans le sang diminue de 8 % chaque heure.
1. Vérifier que u1=1,84 et en donner une interprétation dans le contexte de l’exercice.
1-8 / 100 = 0,92 ; u1 = 0,92 *u0 = 0,92 *2=1,84 .
Au bout d'une heure, le volume de médicament dans le sang vaut 1,84 cm3.
2. a. Pour tout entier naturel n , exprimer un+1 en fonction de un.
un+1 =0,92 un.
b. En déduire la nature de la suite (un). Préciser sa raison et son premier terme.
Suite géométrique de raison 0,92 et de premier terme u0 = 2.
3. Pour que le
médicament soit actif, le volume de médicament présent dans le sang du
malade doit rester supérieur à un certain seuil S ; ce seuil dépend du
malade.
a. À l’aide d’une fonction écrite en langage Python, on se propose de
déterminer, en fonction de S, le nombre maximal d’heures durant
lesquelles le médicament reste actif. Compléter le programme écrit en
Python.
def volMedicament(S) :
u=2
n=0
while u > S
u=u*0,92
n = n+1
return n
b. On s’intéresse au cas d’un malade pour qui ce seuil est estimé à S=1,5 cm3.
Que doit-on saisir pour exécuter la fonction volMedicament afin qu’elle
renvoie le nombre maximal d’heures durant lesquelles le médicament
reste actif chez ce malade ? Quel est alors ce nombre d’heures ?
On doit saisir 1,5.
n
|
2
|
3
|
4
|
un
|
1,69
|
1,56
|
1,43
|
Au bout de 4 heures, le volume de médicament dans le sang est inférieur à 1,5 cm3.
Sujet 32.
Dans le repère ci-dessous, on note Cf la courbe représentative d’une fonction f définie sur l’intervalle [−10 ;2].
On a placé dans ce repère les points A(0 ;2), B(2 ;0) et C(−2 ;0).
On dispose des renseignements suivants :
Le point B appartient à la courbe Cf.
La droite (AC) est tangente en A à la courbe Cf.
La tangente à la courbe Cf au point d’abscisse 1 est une droite parallèle à l’axe des abscisses.
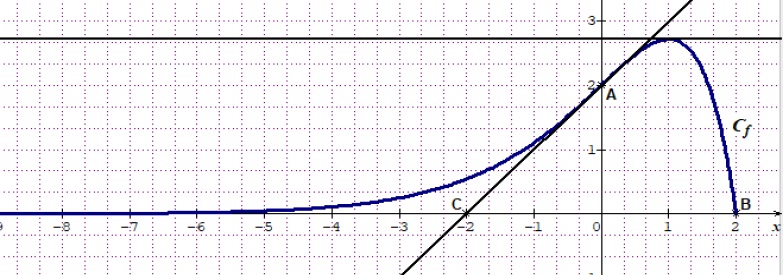
1. Déterminer la valeur de f ′(1).
La tangente à la courbe Cf
au point d’abscisse 1 est une droite parallèle à l’axe des abscisses,
son coefficient directeur est donc nul, c'est à dire f '(1) = 0.
2. Donner une équation de la tangente à la courbe Cf au point A.
Coefficient directeur : +1 ; équation de cette droite tangente en A : y = x +b.
A appartient à cette droite : yA = xA + d ; 2 = 0 +b ; b = 2 et y = x+2.
On admet que cette fonction f est définie sur [−10 ;2] par f(x)=(2−x)ex.
3. Montrer que pour tout réel x appartenant à l’intervalle [−10 ;2], f ′(x)=(−x+1)ex.
On pose u = 2-x et v = ex ; u' = -1 ; v' = ex ; u'v+v'u = -ex +(2-x)ex =(−x+1)ex.
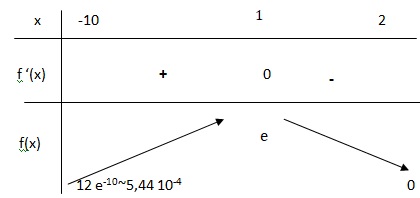
4. En déduire le tableau de variations de la fonction 𝑓 sur l’intervalle [−10 ;2].
ex est toujours positif ;
Si x > 1, f '(x) est négative et f(x) est strictement décroissante.
Si x < 1, f '(x) est positive et f(x) est strictement croissante.
Si x = 1, f '(x) =0 et f(x) présente un maximum.
5. Déterminer une équation de la tangente à la courbe Cf au point B.
Coefficient directeur de la tangente en B : f '(2) =(-2+1)e2 = -e2.
Equation de cette droite : y = -e2x +b.
B appartient à cette droite : yB = -e2xB +b ; 0 = -2e2 +b ; b = 2e2.
y = -e2x +2e2.
|
|
Exercice 4. ( 5 points) Sujet 31 Une culture de pois comporte des pois de couleur « jaune » ou « vert » et de forme « lisse » ou « ridé ».
Le tableau ci-dessous est partiellement renseigné à partir des
observations effectuées sur un grand nombre de pois de cette culture.
|
Nombre de pois jaunes
|
Nombre de pois verts
|
Total
|
Nombre de pois ridés
|
100
|
500
|
600
|
Nombre de pois lisses
|
200
|
9200
|
9400
|
Total
|
300
|
9700
|
10 000
|
1. Compléter le tableau.
On choisit au hasard un pois de la culture et on s’intéresse aux évènements suivants :
J : « le pois est jaune » ;
R : « le pois est ridé ».
L’échantillon étudié est suffisamment important pour être considéré comme représentatif de l’ensemble de la culture de pois.
2. Quelle est la probabilité que le pois soit vert et lisse ?
9200 / 10 000 = 0,92.
3. Calculer la probabilité que le pois soit vert.
9700 / 10 000 = 0,97.
4. Calculer la
probabilité qu’un pois soit jaune sachant qu’il est ridé, et en déduire
la probabilité qu’un pois soit vert sachant qu’il est ridé.
PR(J)=P(J n R) / P(R) =100 / 600 = 1 / 6.
PR(non J)=P( non J n R) / P(R) =500 / 600 = 5 / 6 soit 1 - 1 /6.
5. Calculer PJ(R) et en donner une interprétation dans le contexte de l’énoncé.
PJ(R) = P(J n R) / P(J) =100 / 300 = 1 /3.
La probabilité qu'un pois soit ridé sachant qu'il est jaune est égale à 1 /3.
|
Sujet 32.
La médiathèque d’une petite ville a ouvert ses portes début janvier 2013 et a enregistré 2 500 inscriptions pour l’année 2013.
Elle estime que, chaque année, 80% des anciens inscrits renouvellent
leur inscription l’année suivante et qu’il y aura également 400
nouveaux adhérents.
Pour tout entier naturel n, on peut donc modéliser le nombre d’inscrits
à la médiathèque n années après 2013 par une suite numérique (an) définie par :
a0=2500 et an+1=0,8an+400 .
1. Calculer a1 et a2.
a1 = 0,80a0 +400 =0,8 *2500+400=2400.
a2 = 0,80a1 +400 =0,8 *2400+400=2320.
2. On pose, pour tout entier naturel n, vn=an−2000.
a. Démontrer que (vn) est une suite géométrique de raison 0,8. Préciser son premier terme.
vn+1= an+1-2000 = 0,8an+400 -2000=0,8an-1600 = 0,8(an-2000)=0,8 vn.
vn+1 / vn = 0,8 ; suite géométrique de raison 0,8 et de premier terme v0 = 2500-2000 = 500.
b. Exprimer, pour tout entier naturel n, vn en fonction de n.
vn = v0 x0,8n = 500 x0,8n.
c. En déduire que pour tout entier naturel n, an=500×0,8n+2000.
vn = 500 x0,8n =an−2000 ; an= 500×0,8n+2000.
d. Déterminer le plus petit entier naturel n tel que an ≤ 2010. Interpréter ce résultat dans le contexte de l’exercice.
500×0,8n+2000 < 2010 ; 500×0,8n < 10 ; 0,8n < 10 / 500 ; 0,8n < 0,02
n ln (0,8) < ln( 0,02) ; n > 17,53 soit n > 18..
On vérifie : a17 =500 x0,817 +2000 =2011 ; a18 =500 x0,818 +2000 =2009.
n 2013 +18 =2031, le nombre d'inscrits sera inférieur à 2010.
|
|