Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 19
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1. On considère la fonction f définie sur R par f (x) =2x2+6x-8
Parmi les propositions suivantes, laquelle est juste ?
a) f(x) =2(x-4)(x+1) ; b. f(x) = (2x+8)(2x-2) ; c. f(x) =2(x+4)(x-1) ; d. f(x) =2(x+3)(x-2).
Racine évidente de 2x2+6x-8=0, x = 1 ; a et d sont éliminées.
b ne convient pas, elle donne 4x2. Réponse c.
2.Pour tout réel x,(ex)2 / e−x est égal à :
a) exp(x2+x) ; b) e3x c) e2 d) e−2.
e2x / e-x = e2x+x = e3x. Réponse b.
3. Dans le plan muni d’un repère, soit C la courbe représentative de la fonction g définie sur R
par g(x) = ex. L’équation de la tangente à la courbe C au point d’abscisse 0 est :
a) y = -x-1 ; b) y= -x+1 ; c) y =x+1 d) y= x.
Coefficient directeur de la tangente en x = 0 : f '(0) = e0 = 1.
Ordonnée du point d'abscisse x = 0 : f(0) =1. Ce point appartient à la tangente : y = x+b ; 1 = b. Réponse c.
4. On considère la fonction f définie sur R par f(x) =(-x+1)ex.
On note f ′ la fonction dérivée de la fonction f. Parmi les propositions suivantes, laquelle est juste ?
a) f ′(x) = −xex ; b) f ′(x) = (x − 2)ex ; c) f ′(x) = (−x + 2)ex ; d) f '(x) = xe-x.
On pose u = -x+1 et v = ex ; u' = -1 ; v' = ex.
u'v+v'u =-ex+(-x+1)ex =-xex. Réponse a.
5. Dans le plan muni d’un repère orthonormal, on considère la courbe représentative d’une fonction 𝑓 définie et dérivable sur R.
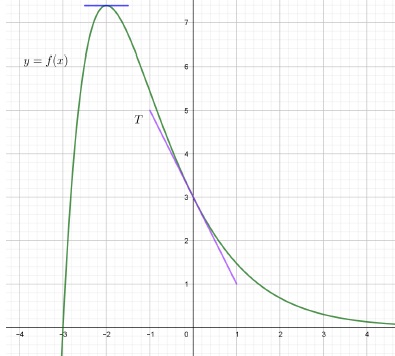
Parmi les propositions suivantes, laquelle n’est pas juste ?
a) f ′(−2)=0 ; b) f ′(3)=−2 faux ; c) f(0)=3 ; d) f '(0)=−2.
Sujet 20.
1. Soit ABC un triangle tel que AB = 6, AC = 3 et l'angle �BAC = p /3.
2. Soit f une fonction telle que, pour tout nombre réel h non nul,
( f (1+h)− f (1) ) / h = h2+3h−1.
Alors f ′(1) est égal à .
a. h2 +3h−1 ; b. −1 ; c. 3 ; d. les données sont insuffisantes pour déterminer f ′(1).
On cherche la limite de ( f (1+h)− f (1) ) / h soit celle de h2+3h−1 quand h tend vers zéro.
Cette limite est égale à -1. Réponse b.
3. Soit f la fonction définie sur R par f (x) = (x +2)ex .
Alors, la fonction f ′ dérivée de f est donnée sur R par :
a. f ′(x) = ex ; b. f ′(x) = (x +3)ex ; c. f ′(x) = (−x −1)ex ; d. f ′(x) = (−x −1)ex / e2x.
On pose u =x+2 et v = ex ; u' = 1 et v' = ex.
u'v +v'u = ex +(x +2)ex = ex(x+3). Réponse b.
4. Soit f une fonction telle que f (2) = 5 et f ′(2) = −1.
Dans un repère, la tangente à la courbe représentative de f au point d’abscisse 2 a pour équation :
a. y = −x −3 ; b. y = −x +3 ; c. y = −x +7; d. y = 5x −11.
Coefficient directeur de la tangente : f '(2) = -1.
Equation de la tangente : y = -x+b.
Le point de coordonnées (x=2 et f(2) =5) appartient à la tangente : 5 = -1*2+b ; b = 7.
y = -x+7. Réponse c.
5. Soit f une fonction définie et dérivable sur R dont la courbe représentative Cdans un repère est la courbe ci-dessous.
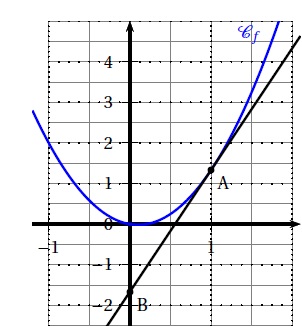
La tangente à la courbe Cf au point A (1 ; 4 / 3) passe par le point B (0 ;- 5 /3). Alors :
a. f ′(1) =1 / 3 ; b. f '(1) = 4 / 3 ; c. f '(1) = -5 / 3 ; d. f '(1) =3.
Coefficient directeur positif de la tangente : (yA-yB) / (xA-xB)= 3 ; f '(1) = 3. Réponse d.
|
|
Exercice 2. ( 5
points) Sujet 19. On administre à un patient un médicament par injection intraveineuse.
La première injection est de 10 ml, puis toutes les heures on lui en injecte 1 ml.
On étudie l’évolution de la quantité de médicament présente dans le sang en prenant le modèle suivant :
on estime que 20 % de la quantité de médicament présente dans le sang est éliminée chaque heure ;
pour tout entier naturel n, on note un la quantité de médicament en ml présente dans le sang au bout de n heures.
Ainsi, u0=10.
1. Justifier que u1=9.
u1 = 10x0,8 +1 = 9.
2. Montrer que, pour tout entier naturel n, un+1=0,8 un+1.
un+1 = (1-20 / 100)un +1 =0,8 un+1.
On donne ci-dessous la représentation graphique de la suite (un) :
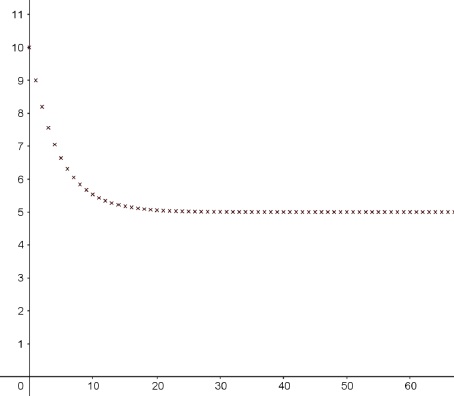
3. Conjecturer la limite de la suite(un).
La suite semble tendre vers 5 mL.
On considère l’algorithme suivant :
U<--10
N<--0
Tant que U >5,1 faire
U<-- 0,8*U+1
N<--N+1
Fin du tant que
Afficher N
4. À quoi cet algorithme sert-il ?
Cet algotithme détermine à partir de quelle valeur de n, un est inférieur ou égal à 5,1.
5. À l’aide de l’extrait du tableau de valeurs de la suite (un) donné ci dessous, donner la valeur de N à l’issue de l’exécution de cet algorithme.

N = 18 à la fin de l'exécution de l'algorithme.
Sujet 20.
Une
entreprise fabrique q milliers d’objets, q ∈ [1 ; 20]. Le coût total de
fabrication, exprimé en euros en fonction de q, est donné par
l’expression :
C(q)= q3−18q2+750q +200.
1. a. Calculer le coût total de fabrication de 5 000 objets.
C(5000) =53 -18 *52+750*5+200=3625 €.
b. Déterminer le coût moyen de fabrication d’un millier d’objets lorsqu’on fabrique 5 000 objets.
3625 / 5 =725 €.
2. Le coût moyen CM(q) de fabrication de q milliers d’objets, exprimé en euros, est donné par l’expression :
CM(q) = C(q) / q = q2−18q +750+ 200 / q..
a. On note C′M la fonction dérivée, sur l’intervalle [1; 20], de la fonction CM.
Montrer que, pour tout q ∈ [1 ; 20], C′M (q)= 2(q −10)(q2 +q +10) /q2.
C'M(q) = 2q-18-200 /q2.
(q −10)(q2 +q +10) =q3+q2+10q-10q2-10q-100 =q3-9q2-100 ;
2(q −10)(q2 +q +10) =2q3-18q2-200 ;
2(q −10)(q2 +q +10) /q2 =2q-18-200 /q2 =C'M(q).
b. Étudier le signe de C′M et dresser le tableau de variation de la fonction CM sur l’intervalle [1; 20].
Solutions de (q −10)(q2 +q +10) =0.
(q2 +q +10) /q2est positif sur [1; 20].
La dérivée a le signe de q-10.
Si q < 10, C'M(q) < 0, CM(q) fonction strictement décroissante.
Si q > 10, C'M(q) > 0, CM(q) fonction strictement croissante.
Si q = 10; C'M(q) = 0, CM(q) est minimale.
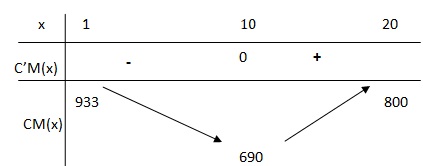
c. Quel est le coût moyen minimal et pour quelle quantité d’objets est-il obtenu ?
Le coût moyen minimal est égal à 690 € pour 10 000 objets vendus.
|
|
Exercice 3. ( 5 points).
Sujet 19.
On considère la fonction f définie sur l’intervalle [−2 ;2] par f(x)=2x3+2x2−2x+3 et 𝐂 sa représentation graphique dans le repère suivant.
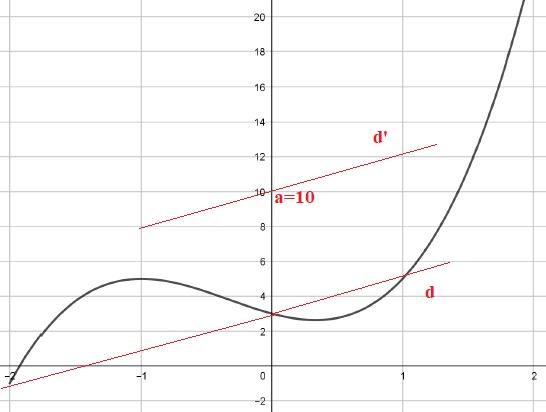
1. On considère la droite d d’équation y =2x+3.
a. Montrer
que déterminer les abscisses des points d’intersection entre la droite
d et la courbe 𝐂 revient à résoudre l’équation 2x(x2+x−2)=0 sur l’intervalle [−2 ;2].
2x3+2x2−2x+3 =2x+3 ; 2x3+2x2−4x =0 ; 2x(x2+x-2)=0
b. Déterminer les coordonnées des points d’intersection entre d et 𝐂.
x = 0 et y =3 ;
x2+x-2=0, solution évidente x = 1, soit y = 5 ; x = -2 et y =-1.
2. On considère la droite d' d’équation y=2x+a où a est un nombre réel.
À l’aide du graphique, donner une valeur de a pour laquelle la droite d' et la courbe 𝐂 ont un seul point d’intersection.
Par exemple a = 10.
3. On note f ′ la fonction dérivée de f.
a. Démontrer que, pour tout nombre réel x appartenant à l’intervalle [−2 ;2] , f '(x)=6(x+1)(x−1/3).
f '(x) =6x2+4x-2 = 2(3x2+2x-1).
Solution évidente de 3x2+2x-1 =0 : x = -1; le produit des deux racines est égal à ac soit -3; l'autre solution est x = 1/3.
3x2+2x-1=3 (x+1)(x-1 /3) et f '(x) =6 (x+1)(x-1 /3)
b. Étudier les variations de f sur l’intervalle [−2 ;2].
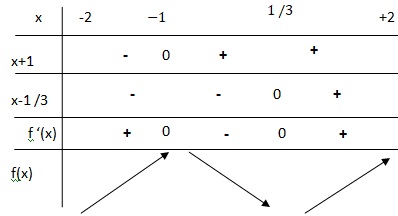
f(x) est strictement décroissante sur [-1 ; 1 /3 ].
f(x) est strictement croissante sur [-2 ; -1] union [1 / 3 ; 2 ].
Sujet 20.
La famille A décide de diminuer de 2% par mois sa quantité de déchets produite par mois à partir du 1er janvier 2020.
Au mois de décembre 2019, elle a produit 120 kg de déchets.
1. Justifier qu’au bout de 2 mois, la famille A aura produit environ 115 kg de déchets.
Au bout d'un mois : 120 x0,98 =117,6 kg ; au bout de 2 mois : 117,6 x0,98 =115,248 kg.
On admet que la quantité de déchets produits chaque mois conserve la même évolutio toute l’année.
On modélise l’évolution de la production de déchets de la famille A par la suite de terme général an, où an représente la quantité, en kg, de déchets produits par la famille A n mois
après décembre 2019.
Ainsi, a0 représente la quantité de déchets produits durant le mois de décembre 2019, a1 représente la quantité de déchets produits durant le mois de janvier 2020, etc.
2. a. Déterminer la nature de la suite (an).
an+1 / an = 0,98, suite ghéométrique de raison 0,98 et de premier terme 117,6.
b. Pour tout entier naturel n, exprimer an en fonction de n.
an = 117,6 x0,98n.
c. Déterminer la quantité totale de déchets que produira la famille A durant l’année 2020.
On arrondira le résultat à l’unité.
S =117,6(1-0,9812) / (1-0,98) =1265,86 kg.
d. On donne le programme ci-dessous.
def S(n):
U = 128
S = 0
for k in range (n):
U = 0.98*U
S = S + U
return (S)
Que représente le résultat renvoyé par la fonction si on entre l’instruction S(6) ?
S(6) représente la quantité de déchets produit par la famille pendant les six premiesr smois de l'année.
|
|
Exercice 4. ( 5 points) Sujet 19 Une résidence de vacances propose uniquement deux formules :
la formule « pension complète » dans laquelle 3 repas par jour sont fournis ;
la formule « demi-pension » dans laquelle sont fournis uniquement le petit déjeuner et le dîner.
Pour l’année 2018, 65 % des clients ont choisi la pension complète ; les autres ont choisi la formule « demi-pension ».
Parmi les clients qui ont choisi la demi-pension, 30 % ont réservé
l’option « ménage » en fin de semaine. De plus, 70 % des clients qui
ont choisi la pension complète ont réservé l’option ménage.
On choisit un client au hasard parmi ceux de l’année 2018 et l’on considère les évènements suivants :
C : le client a choisi la formule « pension complète » ;
M: le client a choisi l’option « ménage ».
1. Recopier sur la copie et compléter l’arbre pondéré.
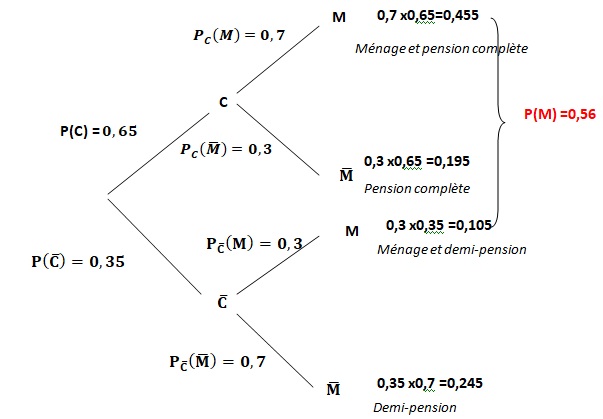
2. Calculer P(C∩M).
P(C∩M) =0,65 x0,7 =0,455.
3. Montrer que la probabilité que le client ait réservé l’option ménage est égale à 0,56.
P(M)=P(C n M) + P(non C n M) = 0,455 +0,35 x0,3 =0,56.
4. Calculer la probabilité que le client ait choisi la formule « pension complète » sachant qu’il a réservé l’option ménage.
PM(C) = P(M n C) / P(M) =0,455 / 0,56 =0,8125.
5. Voici la grille de tarifs de la résidence de vacances pour l’année 2018:
Une semaine de pension complète : 800 €.
Une semaine de demi-pension : 650 €
Option ménage : 50 €.
On note X la variable aléatoire égale au montant payé par un client de 2018.
Calculer P(X = 850).
Pension complète et ménage : P(X = 850)=0,455
|
Sujet 20.
Pierre
joue à un jeu dont une partie est constituée d’un lancer d’une
fléchette sur une cible suivi d’un tirage au sort dans deux urnes
contenant des tickets marqués « gagnant » ou « perdant »
indiscernables.
• S’il tire un ticket marqué « gagnant », il pourra recommencer une partie.
• S’il atteint le centre de la cible, Pierre tire un ticket dans l’urne U1 contenant exactement neufs tickets marqués « gagnant » et un ticket marqué « perdant ».
• S’il n’atteint pas le centre de la cible (donc même s’il n’atteint pas la cible), Pierre tire un ticket dans l’urne U2 contenant exactement quatre tickets marqués « gagnant » et six tickets
marqués « perdant ».
Pierre atteint le centre de la cible avec une probabilité de 0,3.
On note les événements suivants :
C : « Pierre atteint le centre de la cible » ;
G : « Pierre tire un ticket lui offrant une autre partie ».
1. Recopier l’arbre pondéré ci-dessous et justifier la valeur 0,9.
Dans l'urne 1 il y a 9 tickets gagnants sur 10 tickets.
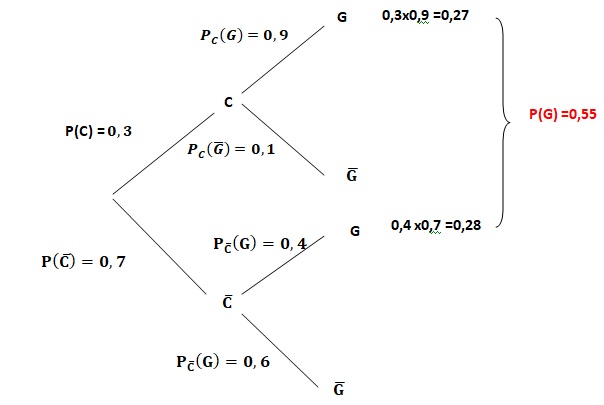
2. Compléter sur la copie l’arbre pondéré en traduisant les données de l’exercice.
3. Calculer la probabilité de l’événement C ∩G.
P(C ∩G) =0,3 x0,9 = 0,27.
4. Montrer que la probabilité qu’à l’issue d’une partie Pierre en gagne une nouvelle est égale à 0,55.
P(C ∩G) +P(non C n G) = 0,27 +0,7 x0,4 =0,55.
5. Sachant que
Pierre a gagné une nouvelle partie, quelle est la probabilité qu’il ait
atteint le centre de la cible ? Arrondir le résultat à 10−3.
PG(C) = P(G n C) / P(G) = 0,27 / 0,55 =0,491.
.
|
|