Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 15
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1. On considère la suite (un) définie par u0=100 et pour tout entier naturel n, un+1=un−13 / 100un . Quelle est la nature de la suite (un) ?
A) géométrique de raison 1
B) arithmétique de raison −13 /100
C) géométrique de raison 1 et arithmétique de raison −13100
D) géométrique de raison 0,87. vrai.
un+1 =(1-13 /100)un = 87 / 100 un = 0,87 un.
2.On considère la variable aléatoire X qui prend les valeurs xi pour i entier naturel allant de 1 à 5. La loi de probabilité incomplète de la variable aléatoire X est donnée ci-dessous :
X=xi
|
-6
|
-3
|
0
|
3
|
x5
|
P(X=xi)
|
0,2
|
0,1
|
0,2
|
0,4
|
0,1 |
L’espérance de la variable aléatoire 𝑋 est égale à 0,7.
Quelle est la valeur x5 prise par la variable aléatoire 𝑋 ?
A) 6 ; B) 1 ; C) 10 vrai; D) 100.
E(X) = -6*0,2-3*0,1+0+3*0,4+0,1x5 = 0,7.
-0,3+0,1x5 = 0,7 ; x5=10.
3. Soit f la fonction dérivable définie sur ]−73 ; +∞[ par f(x) =(2x+3) /(3x+7) et f ′ sa fonction dérivée.
A) f ' (x)=2 /3 ; B) f ′(x)=23 /(3x+7)² ; C) f ′(x)=5/ (3𝑥+7)2 ;D) f ′(x)=5 / (3𝑥+7).
On pose u =2x+3 et v = 3x+7 ; u' =2 ; v' = 3.
(u'v-v'u) / v2 =(2(3x+7)-3(2x+3)) / (3x+7)2 =5 / (3x+7)2 ; réponse C.
4. De
2017 à 2018, le prix d’un article a augmenté de 10 %. En 2019, ce même
article a retrouvé son prix de début 2018. Quelle a été l’évolution du
prix entre 2018 et 2019 ?
A) une baisse de 10 %
B) une baisse de plus de 10 %
C) on ne peut pas savoir
D) une baisse de moins de 10 %. vrai.
On appelle x le pourcentage de diminution en 2019.
Prix initial : 1 en 2017 ; prix début 2018 : 1,1 ; prix début 2019 : 1,1(1- x / 100) = 1.
1-x /100= 1 / 1,1 ~0,909 ; x /100 = 1-0,909 ~0,091 ; x =9,1 %...
5. Soit (un) la suite définie par u0=4 et pour tout entier naturel n par un+1 = 3un-5.
On souhaite qu’à la fin de l’exécution de l’algorithme, la valeur contenue dans la variable u soit celle de u5 . Quel algorithme doit-on choisir ?
 Sujet 16.
Sujet 16.
1. EFG est un triangle tel que EF = 8, FG = 5 et l'angle ÊFG =3p/4.
Alors le produit scalaire suivant est égal à :
a) 20√2 ; b) −20√2 vrai ; c) 20√3 ; d) −20√3.
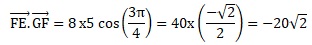
2. Dans un repère orthonormé, on a tracé la courbe représentative d’une fonction f et sa tangente au point A d’abscisse 0.
On note f ′ la dérivée de la fonction f. On a :
a) f ′(0) = 2 ; b) f ′(0) = − 1 ; c) f ′(2) = −1; d) f ′(−2) = 0.
Coefficient directeur de la tangente en x = 0 : -1= f '(0).
réponse b.
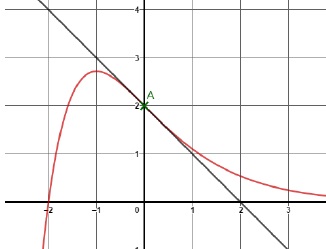
3. On se place dans un repère orthonormé du plan. On a tracé ci-dessous la courbe représentative d’une fonction f définie sur R.
L’équation f(x) = −3 a pour solution(s) :
a) 3 ; b) 0 ; c) −3 ; d) 0 et 1.vrai.
4. On se place dans un repère orthonormé. Une équation du cercle de centre B( 2 ; 3) et de rayon 4 est :
a) (x+2)²+(y+3)²=4
c) (x−2)²+(y−3)²=16. vrai
b) (x−2)²+(y−3)²=4
d) (x+2)²+(y+3)²=16.
5. Un vecteur normal à la droite d’équation cartésienne −3𝑥−2𝑦+5=0 a pour coordonnées :
a. (2 ; 3 ) ; b. (3 ; -2) : c.( -3 ; 2) ; d(3 ; 2) vrai.
Equation cartésienne de la droite :3x+2y-5=0.
|
|
Exercice 2. ( 5
points) Sujet 15. Un restaurant propose à sa carte deux desserts différents :
le premier dessert est un assortiment de macarons, et est choisi par 40 % des clients,
le second dessert est une part de tarte, et est choisie par 30 % des clients.
Les autres clients ne prennent pas de dessert. Aucun client ne prend plusieurs desserts.
Le restaurateur a remarqué que parmi les clients ayant pris comme
dessert un assortiment de macarons, 70 % prennent un café, que parmi
les clients ayant pris comme dessert une part de tarte, 40 % prennent
un café et que parmi les clients n’ayant pas pris de dessert, 90 %
prennent un café. On interroge au hasard un client de ce restaurant.
On note : ▪ M l’évènement : « Le client prend un assortiment de macarons. »
▪ T l’évènement : « Le client prend une part de tarte. »
▪ N l’évènement : « Le client ne prend pas de dessert. »
▪ C l’évènement : « Le client prend un café. »
1. Construire un arbre de probabilités décrivant la situation.
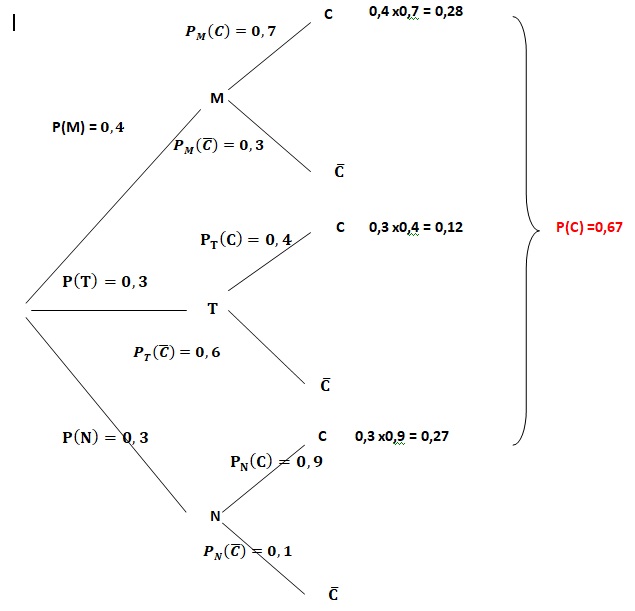
2. Définir par une phrase les probabilités 𝑃(𝑇∩𝐶) et 𝑃𝐶(𝑀) (on ne demande pas de les calculer).
𝑃(𝑇∩𝐶) : probabilité que lle client prenne une tarte et un café.
𝑃𝐶(𝑀) : probabilité que le client prenne un macaron sachant qu'il a pris un café.
3. Calculer 𝑃(𝑇∩𝐶) puis 𝑃(𝐶).
𝑃(𝑇∩𝐶) =0,3 x0,4 = 0,12.
4. On rencontre un
client ayant pris un café. Quelle est la probabilité qu’il ait pris une
part de tarte ? On donnera le résultat sous forme d’une fraction
irréductible.
PC(T) =P(C n T) / P(C) =0,12 / 0,67 = 12 / 67.
Sujet 16.
Partie A
On considère la fonction polynôme du second degré 𝑷 définie sur R par : P(x) = x2-7x+6.
1) Résoudre l’équation P(x) = 0.
x2-7x+6 =0 ; discriminant : (-7)2 -4*1*6=25 = 52.
Solutions x = (7±5) / 2 soit x = 6 et x = 1
2) Étudier le signe de P sur R.
P(x) = (x-6)(x-1).

Partie B.
On considère la fonction polynôme du troisième degré f définie sur R par : f(x))=2x3−21x2+36x
1) Calculer la dérivée f ′ de f et vérifier que f ′((x)= 6P(x).
f '(x) =6x2-42x+36 =6(x2-7x+6) = 6 P(x).
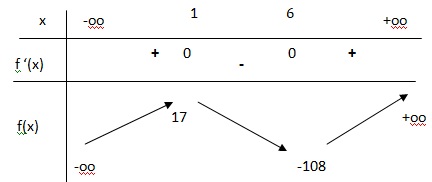
2) Etudier les variations de la fonction f.
3) On se place dans
un repère du plan. Déterminer une équation de la tangente T à la courbe
représentative de f au point B d’abscisse 3.
Coefficient directeur de T : f '(3) =6*9-42*3+36 = -36
Equation de la tangente T : y =-36x+b.
Ordonnée de B : f(3) =2*27-21*9+36*3= -27.
B est sur la tangente T : -27 = -36*3+b ; b =81
y =-36x+81.
|
|
Exercice 3. ( 5 points).
Sujet 15.
On appelle orthocentre d’un triangle le point de concours de ses trois hauteurs.
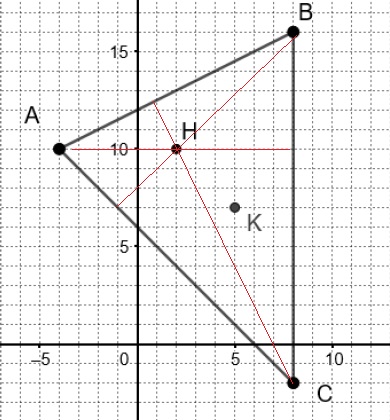
Dans le plan muni d’un repère orthonormé, on considère les points A(−4;10), B(8;16) , C(8;−2), H(2 ;10) et K(5 ;7).
1. Montrer que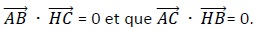

2. Que représente le point H pour le triangle ABC ?
HC est la hauteur issue de C, elle est perpendiculaire à AB.
HB est la hauteur issue de B, elle est perpendiculaire à AC.
H est l'orthocentre du triangle ABC.
3. Montrer que K est le centre du cercle passant par les sommets du triangle ABC
KA( 5-(-4) ; 7-10) soit ( 9 ; -3) ; KA2 =92 +(-3)2 = 90.
KB( 5-8 ; 7-16) soit ( -3 ; -9) ; KA2 =(-9)2 +(-3)2 = 90.
KC( 5-8 ; 7-(-2)) soit ( -3 ; 9) ; KA2 =92 +(-3)2 = 90.
KA = KB= KC, K est le centre du cercle circonscrit au triangle ABC.
4. On admet que G, le centre de gravité du triangle ABC, est le point qui vérifie
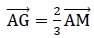 où M est le milieu du segment [BC]. Déterminer les coordonnées de G. où M est le milieu du segment [BC]. Déterminer les coordonnées de G.
M((xB +xC) / 2 ;( yB +yC) / 2 ) soit( 8 ; 7)
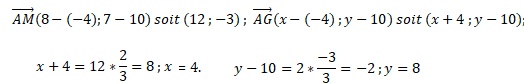
5. Montrer que les points G, H et K sont alignés.
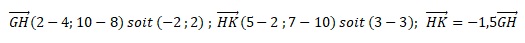
Ces vecteurs étant colinéaires, les points G, H et K sont alignés.
Sujet 16.
Une
chaîne de salons de coiffure propose à ses 5000 clients qui viennent
pour une coupe deux prestations supplémentaires cumulables :
- une coloration naturelle à base de plantes appelée « couleur-soin »,
- des mèches blondes pour donner du relief à la chevelure, appelées « effet coup de soleil ».
Il apparaît que 2000 clients demandent une « couleur-soin ». Parmi ceux
qui ne veulent pas de « couleur soin », 900 demandent un « effet coup
de soleil ». Par ailleurs, 650 clients demandent une « couleur soin »
et un « effet coup de soleil ».
On notera C l’évènement « le client souhaite une « couleur-soin ».
On notera E l’évènement « le client souhaite un « effet coup de soleil ».
1) Recopier sur votre copie et compléter le tableau suivant :
|
C
|
non C
|
Total
|
E
|
650
|
900
|
1550
|
non E
|
1350
|
2100
|
3450
|
Total
|
2000
|
3000
|
5000
|
2) On interroge un client au hasard parmi les 5000 clients.
a. Quelle est la probabilité qu’il ait choisi les deux prestations : « couleur soin » et « effet coup de soleil » ?
P(C n E) =650 / 5000 =0,13.
b. Calculer PE(non C).
PE(non C) =P(E n non C) / P(E) =900 / 1550 = 18 / 31~0,581.
3) On a des prix différents suivant la prestation fournie. On appelle X le prix payé en euros par chaque client.
|
coupe seule
|
coupe avec "couleur soin"
|
coupe avec "effet coup de soleil" |
coupe avec "effet coup de soleil" et "couleur soin"
|
valeur de k (€)
|
20
|
50
|
65
|
80
|
P(X=k)
|
1-0,27-0,18-0,13=0,42
|
1350 / 5000 = 0,27
|
0,18
|
0,13
|
Après avoir recopié et complété le tableau, calculer l’espérance de X.
X = 20 *0,42 +50 *0,27 +65 *0,18 +80 *0,13 =44 €.
|
|
Exercice4. ( 5 points) Sujet 15 Une entreprise produit du tissu.
Le coût total de production (en €) de l'entreprise est modélisé par la fonction
C(x)=15x3−120x2+500x+750 où x est la longueur de tissu fabriqué exprimée en kilomètre, x étant compris entre 0 et 10.
Chaque kilomètre de tissu est vendu 680 €.
On note B(x) le résultat de l'entreprise, c’est-à-dire la différence
entre la recette et le coût de production, pour la vente de x
kilomètres de tissu.
1. Quel est le résultat de l’entreprise pour la vente de 3 kilomètres de tissu ?
C(3) =15*27-120*9+500*3+750=1575 €.
Prix de vente : 680 *3 =2040 €.
Résultat : 2040 -1575 =465 €.
2. Montrer que : B(x)=−15x3+120x2+180x−750.
B(x) =680x-(15x3−120x2+500x+750)=−15x3+120x2+180x−750.
3. Donner une expression de B'(x)), où B' est la fonction dérivée de la fonction B.
B'(x) = -45x2+240x+180 = 15 (-3x2+16x+12)
4. Dresser le tableau de signes de B(x) sur [0;10] puis le tableau de variations de la fonction B.
5. Combien de kilomètres de tissu l’entreprise doit-elle produire afin d’obtenir un résultat maximal ?
-3x2+16x+12 = 0 ; discriminant : 162-4*12*(-3)=400 =202.
Solution retenue : (-16-20)/ (-6) =6.
B'(x) >0 pour x appartenant à [0 ; 6[; B(x) croissante.
B'(x) < 0 pour x appartenant à ]6 ; 10]. B(x) décroissante.
B'(x) =0 pour x=6 ; B(x) présente un maximum pour x = 6.

|
Sujet 16.
Un apiculteur souhaite étendre son activité de production de miel à une nouvelle région.
Au printemps 2019, il achète 300 colonies d’abeilles qu’il installe dans cette région.
Il consulte les services spécialisés de la région et s’attend à perdre
8% des colonies chaque hiver. Pour maintenir son activité et la
développer, il prévoit d’installer 50 nouvelles colonies chaque
printemps, à partir de l’année suivante.
1) On donne le programme suivant écrit en langage Python :
def algo( ) :
C = 300
N = 0
while C < 400 :
C = C*0.92+50
N = N+1
return(N)
a. Recopier et compléter en ajoutant des colonnes, le tableau ci-dessous qui reproduit l’avancement du programme pas à pas :
Les valeurs seront arrondies à l’entier le plus proche.
C
|
300
|
326
|
0,92*326+50
=350
|
0,92*350+50
=372
|
0,92*372+50
=392
|
0,92 *392+50
=411
|
C < 400 ?
|
vrai
|
vrai
|
vrai
|
vrai
|
vrai
|
faux.
|
b. Quelle est la valeur de N renvoyée par le programme ?
Interpréter cette valeur dans le contexte de l’exercice.
N =5, l'apiculteur doit attendre 5 ans pour avoitr 400 ruches.
Le nombre de colonies est modélisée par une suite. On note Cn une estimation du nombre de colonies au printemps de l’année 2019+n .
Ainsi c0=300 est le nombre de colonies au printemps 2019.
On admet que pour tout entier naturel n, on a : cn+1=0,92cn+50
2) La suite (cn), est-elle arithmétique ? La suite (cn) est-elle géométrique ?
cn+1-cn=(0,92-1)cn+50, n'est pas une constante : la suite n'est pas arithmétique.
cn+1/ cn=0,92+50 /cn n'est pas une constante ; la suite n'est pas géométrique.
3) On admet que cn=625−325 ×0,92n pour tout entier naturel n.
L’apiculteur pourra-t-il atteindre les 700 colonies ?
325 ×0,92n > 0.
L'apiculteur ne pourra pas atteindre 700 colonies.
|
|