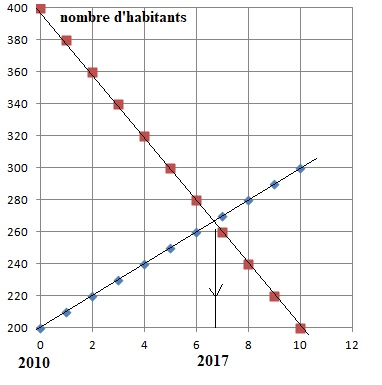
Suites arithmétique et géométrique, mathématiques, classe de première technologique. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . .. ..... Suite arithmétique. 1. En 2010, le village A compte 200 habitants et gagne à partir de cette date 10 habitants par an. Le village B compte 400 habitants en 2010 et perd 20 habitants par an. A partir de quelle date A sera t-il plus peuplé que B ? Nombre d'habitants du village A  : en 2011 : 200 +10 = 210 ; en 2012 : 210 +10 = 220 = 200 +2 x10. en 2013 : 220 +10 = 230 = 200 +3 x10. en 2010 + n : 200 +10 n. Nombre d'habitants du village B  : en 2011 : 400 -20 = 380 ; en 2012 : 380 -20 = 360 = 400 -2 x20. en 2013 : 360 -20 = 340 = 400 -3 x20. en 2010 + n : 400 -20 n. A sera  plus peuplé que B à partir de : 200 +10 n > 400 -20 n. 10n +20 n > 400-200 ; 30 n > 200 ; n > 200 / 30 ; n > 20 / 3 ; (20 /3~7 soit en 2017 ). Solution utilisant un graphique. 2. La suite (un) définie par : un = 7 − 9n est-elle arithmétique ? Si la réponse est oui, préciser la raison. un+1 = 7 -9(n+1) = 7 -9n-9 = -2-9n. un+1 -un = -2-9n -(7-9n) = -2-9n-7 +9n = -9. un+1 -un est égale à un nombre constant, donc la suite est arithmétique. un+1 =un -9. La raison est égale à r = -9. 3. Considérons la suite arithmétique (un) tel que u5 = 7 et u9 = 19 . a) Déterminer la raison et le premier terme de la suite (un). u1 = u0 +r ; u2 = u1 +r =u0 +2r ;  u5 = u0 + 5r =7 ; u9 = u0 + 9r =19 ; u9 - u5 = u0 + 9r -(u0 + 5r) =9 r-5 r = 4 r ; 19-5 = 4 r ; 14 =4 r ; r = 14 / 4 ; r = 3,5. 7 = u0 +5 r = u0 +5 x3,5  ; 7 =u0 +17,5 ; u0 = 5 -17,5 ; u0 = -12,5. b) Exprimer un en fonction de n. un = u0 + 3,5 n. 4. On considère la suite arithmétique (un) de premier terme u0 = 3 et de raison 2,4. 4.a. Alors u20 est égal à :   62,4 ;  108 ;  48 ;  51. u20 =u0 +20 x2,4 =3+ 48 =51. 4.b. On utilise une feuille de calcul pour déterminer les termes de la suite (un). A B C D E F G H I 1 n 0 1 2 3 4 5 6 7 2 un 3 5,4 3 Sn 3 8,4 Quelle formule a-t-on entrée dans la cellule C2 qui, recopiée vers la droite, permet de calculer les termes successifs de la suite (un) ?   =$B$2+2,4 ;  =B2+2,4 vrai ;  =$B2+2,4 ;  =B2*2,4. 4.c. On souhaite calculer la somme S7 = u0+u1+· · ·+u7 des 8 premiers termes de!a suite (un). Quelle formule a-t-on entrée dans la cellule C3 qui, recopiée vers la droite, permet de calculer S7 ?   =B3+C3 ;  =Somme(B2 :C2) ;  =C2+$B3 vrai ;  =B2+C2. .. ... . . Suite géométrique. 1. Considérons la suite géométrique (un) tel que u4 = 8 et u7 = 512 . Déterminer la raison et le premier terme de la suite (un). u1 = q u0 ; u2 = q u1=  q q u0 = q2 u0 ; u4 = q4u0 ;  u7 = q7u0 ; u7 / u4 = q7 / q4 = q3 ; 512 / 8 = q3 ; 64 = q3 ; q = 4. u0 = u4 / q4=8 / 44 =8 /256 =1 / 32. 2. On considère la suite géométrique (vn) de raison 2 telle que v5 = 96. Alors v0 est égal à : v5 = v0 x25 ; v0 = v5 /25=96 / 32 =3. 3. La municipalité met en place une campagne de communication et prévoit que le nombre de visiteurs du parc augmentera de 5% chaque mois à partir de mai 2017. On modélise le nombre mensuel de visiteurs du parc à l’aide d’une suite (un). Ainsi u0 représente le nombre de visiteurs en mai 2017 (u0= 1520), u1 représente le nombre de visiteurs en juin 2017, etc. Afin d’étudier l’évolution de la fréquentation du parc, la municipalité utilise la feuille decalcul automatisé suivante : 1. Quelle formule peut-on entrer dans la cellule C2 de sorte que, recopiée vers la droite sur la plage C2:H2, elle permette d’afficher les estimations du nombre de visiteurs par mois ? =B2*1,05 2. Utilisation de la suite (un). a. Déterminer une estimation du nombre de visiteurs en juin 2017. b. Indiquer, sans justification, la nature de la suite (un). Donner la valeur de sa raison. Suite géométrique de premier terme u0 = 1520 et de raison 1,05. c. Exprimer un en fonction de n, pour tout entier naturel 􀝊 un = u0 x1,05n = 1520 x1,05n. d. Déterminer une estimation du nombre de visiteurs dans ce parc en octobre 2017.  n = 5 ; u5 = 1520 x1,055 =1940. 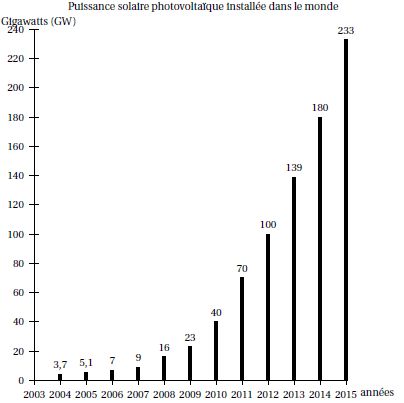L’énergie photovoltaïque voit son coût baisser de façon importante depuis plusieurs années, ce qui engendre une croissance forte de ce secteur. L’évolution de la puissance solaire photovoltaïque installée dans le monde entre fin 2004 et fin 2015 est résumée dans le graphique ci-dessous : Pn+1 e 1. Calculer les pourcentages d’augmentation annuels entre 2013 et 2014 ainsi qu’entre 2014 et 2015 (arrondir à 10−1). (180-139) / 139 * 100 = 29,5 % ; (233-180) / 180 * 100 = 29,4 % . 2. On se propose d’estimer la puissance solaire photovoltaïque installée dans le monde dans les 15 ans à venir, si le taux de croissance annuel reste constant et égal à 30%. On note Pn la puissance solaire photovoltaïque installée dans le monde, en GW, à la fin de l’année 2015+n. On a ainsi P0 = 233. a. Calculer P1 puis P2( arrondir à 10−1). P1 = P0(1+0,30) = 1,3 P0 = 1,3 *233 =302,9 GW. P2 = 1,3 P1 = 1,32P0 =1,32 *233 =393,8 GW. b. Exprimer Pn+1 en fonction de Pn. Pn+1 = 1,3 Pn.  En déduire la nature de la suite (Pn) et donner ses éléments caractéristiques. Suite géométrique de raison 1,3 et de premier terme 233. d. Exprimer Pn en fonction de n. Pn = 233 x 1,3n. e. Calculer la puissance solaire photovoltaïque, en GW, installée dans le monde fin 2025 (arrondir à l’unité).  n=10 ; P10 = 233 x 1,310 = 3212 GW. f. Quel est le pourcentage global d’augmentation de cette puissance solaire mondiale entre 2015 et 2025 (arrondir à l’unité) ? (3212-233) / 233 =12,7854 ( ~1279 %) 3. On veut déterminer l’année durant laquelle la puissance solaire photovoltaïque installée dans le monde atteindrait 16 000 GW. Pour atteindre cette puissance, les panneaux photovoltaïques occuperaient au sol l’équivalent d’un carré de 400 km de côté et suffiraient pour produire toute l’électricité consommée dans le monde (consommation domestique, industrielle et des transports.   a. On considère l’algorithme ci-dessous. Recopier et compléter les lignes 3 et 7 afin que cet algorithme réponde à la question posée. 1/ Affecter à N la valeur 0 2/ Affecter à P la valeur 233 3/ Tant que P<16000 4/ Affecter à N la valeur N +1 5/ Affecter à P la valeur P ×1,30 6/ Fin Tant que 7/ Afficher N +2015. N 15 16 17 P 233 x1,315=11926 233 x1,316=15504 233 x1,317=20155 P <16000 Faux Faux Vrai b. En faisant tourner cet algorithme complété, déterminer l’année durant laquelle la puissance solaire photovoltaïque installée dans le monde dépasserait 16 000 GW. Après son installation, un lundi matin, un aquarium contient 280 litres d’eau et des poissons. Par évaporation, le volume d’eau dans l’aquarium diminue de 2% par semaine. Compte tenu du nombre de poissons, cet aquarium doit contenir en permanence au minimum 240 litres d’eau. Partie A. 1. Quel volume d’eau restera-t-il dans l’aquarium au bout d’une semaine ? 280 x 0,98 = 274,4 L. 2. Est-il vrai qu’au bout de deux semaines, exactement 4% du volume d’eau initial se seront évaporés ? Justifier. Au bout de deux semaines, il reste : 274,4x 0,98 = 268,912 L. 280 x0,96 = 268,8 L diffère de 268,912 L ; l'affirmation est fausse. 3. Vérifier qu'au bout de 8 semaines le volume d’eau dans l’aquarium deviendra insuffisant. 280 x0,98n ~238, valeur inférieure à 240. Au bout de 8 semaines, le volume d'eau est insuffisant.. Partie B. On ajoute chaque lundi matin, en une seule fois, 5 litres d’eau pour compenser l’évaporation hebdomadaire de 2%. On note u0 le volume initial d’eau en litres dans l’aquarium. Ainsi u0 = 280. Pour tout entier naturel n supérieur ou égal à 1, on note un le volume d’eau dans l’aquarium, en litres, n semaines après son installation, immédiatement après l’ajout hebdomadaire des 5 litres d’eau. 1. Vérifier que u2 = 278,812. u1 = 280 x0,98 +5 =279,4 L. u2 = 279,4 x0,98 +5 =278,812 L. 2. Justifier que pour tout entier naturel n, un+1 = 0,98un +5. Chaque semaine on ajoute 5 L d'eau et il s'évapore 2 % du volume d'eau initial. un+1 = 0,98un +5. 3. Montrer que la suite (un) n’est pas géométrique. un+1 / un =0,98 + 5 / un. un+1 / un  n'est pas constant : la suite n'est pas géométrique. Exercice 3. En 2019, Adam est embauché par une entreprise qui lui propose un salaire mensuel net de 1500 €. Son salaire net augmentera de 50 € au premier janvier de chaque année suivante. On note u la suite qui modèlise le salaire mansuel au cours de l'année 2019 +n. Ainsi u(0) = 1500 et u(1) = 1550. 1. Calculer le salaire mensuel net en 2021. u(2) = u(1) +50 = 1550 +50 = 1600 €. 2. Etablir une relation entre u(n+1) et u(n) et préciser la nature de la suite. u(n+1) = u(n) +50 ; suite arithmétique. 3. Quel est le sens de variation de la suite ? Justifier. u(n+1) -u(n) = 50, valeur positive. u(n+1) > u(n), suite croissante. Au cours de l'année 2019, Alice est embauchée par une entreprise qui lui propose un salaire mensuel net de 1400 €. Son salaire net augmentera de 4 % au premier janvier da chaque année suivante. On note v la suite qui modèlise le salaire net d'Alice au cours de l'année 2019 +n. 4. Quelle est la nature de la suite v ? Suite géométrique. v(n+1) = 1,04 v(n) avec v(0) = 1400. 5. A partir de quelle année le salaire d'Alice dépassera t-il pour la première fois celui d'Adam ? n 2019 (n = 0) n=1 (2020) n=2 (2021) n=3 ( 2022) n=4 (2023) 2024 2025 2026 2027 u(n) 1500 1500 +50 = 1550 1550 +50 =1600 1600+50=1650 1700 1750 1800 1850 1900 v(n) 1400 1400 x1,04 =1456 1456 x1,04 =1514,24 1514,24 x1,04=1574,81 1637,8 1703,31 1771,44 1842,30 1916 Exercice 4. On s'intéresse à la population d'une ville et on étudie plusieurs modèles d'évolution de cette population. En 2018, la ville comptait 15 000 habitants. 1. Modèle 1. On fait l'hypothèse que le nombre d'habitants augmente de 1000 par an. On note un le nombre d'habitants pour l'année 2018 +n. Ainsi u0 = 15 000. a. Calculer u1 et indiquer ce que représente u1. u1 = u0 +1000 = 15 000 + 1000 = 16 000 En 2019 la ville compte 16 000 habitants. b. Donner la nature de la suite sans justification. Suite arithmétique. c. On considère l'algorithme ci-dessous : N=0 U=15000 while U < 30000 : U = U+1000 N=N+1 A la fin de l'exécution de cet algorithme N = 15. Interpréter cette valeur dans le contxte de l'exercice. En 2018+15 = 2033, la ville comptera 33 000 habitants. 2. Modèle 2. On fait l'hypothèse que le nombre d'habitants augmente de 4,7 % par an. On note vn le nombre d'habitants pour l'année 2018+n. Ainsi v0 = 15 000. a. On admet que la suite est géométrique. Déterminer sa raison. 100 + 4,7 = 104,7. Le coefficient multiplicateur ( raison) est égal à 1,047. b. Calculer selon ce modèle, le nombre d'habitants en 2023 ( arrondir à l'unité). 2019 2020 2021 2022 2023 15 000 x1,047=15 705 15705 x1,047 =16443 17 216 18 025 18872 Exercice 5. Un responsable commercial du service vélo à assistance électrique ( VAE) doit proposer une estimation du nombre de vélos à produire pour les années à venir. En 2018 l'entreprise a réalisé 4500 ventes de VAE. Ce responsable estime que le nombre de ventes progressera de 22 % chaque année. On note vn le nombre de VAE vendu par l'entreprise en 2018 +n. Ainsi v0 = 4500. 1. Compléter la troisième ligne du tableau suivant : A B C D E 1 Rang de l'année n 0 1 2 3 2 Nombre de ventes vn 4500 4500 x1,22 =5490 5490x1,22=6698 6698 x1,22=8171 2. Exprimer vn+1 en fonction de vn. 100 +22 = 122 ; coefficient multiplicateur 1,22.. vn+1 = 1,22 vn. 3. Donner la nature de la suite en précisant sa raison. vn+1 / vn = 1,22. Suite géométrique. 4. Le responsable souhaite connaître le nombre d'années nécessaire pour que les ventes de VAE dépassent 20 000 unités. Il a préparé un script en langage python. Compléter ce script donnant la réponse au problème. def temps_attente() v = 4500 n = 0 while v < 20 000 : v = v * 1,22 n=n+1 return n. 5. Déterminer la valeur renvoyée par ce programme. . 2021 2022 (n=3) 2023(n=4) 2024(n=5) 2025(n=6) 2026 (n=7) 8171 8171 x 1,22 =9 969 9 969 x1,22 =12 162 12 162 x1,22 =14 837 18101 22084 v < 20 000 vrai vrai vrai vrai Faux . . . .   Exercice 6. 5 points. En 2019 le chiffre d'affaires d'un restaurant gastronomique était de 300 000 €. On modèlise ce chiffre pendant l'année 2019 +n par le n-ième terme de la suite (un) définie par : u0 = 300 et un+1=1,2 un -50 ( en milliers d'euros). 1. Montrer que selon ce modèle, le chiffre d'affaires sera de 310 000 € en 2020. u1 = 1,2 x u0-50 =1,2 x 300-50 =310 milliers d'euros ( 310 000 € ) 2. Calculer u2 et interpréter le résultat. u2 = 1,2 x u1-50 =1,2 x 310-50 =322 milliers d'euros ( 322 000 € ) 3. Faire une conjecture sur le sens de variations de la suite. Expliquer la démarche. un+1 - un =1,2 un -50 -un =0,2 un -50. Or un > u0 ; 0,2 un > 50 ; un+1 - un >0 ; un+1 > un . La suite est croissante. Ou bien : u0 = 300 ; u1 = 310 ; u2 = 322 ; u3 = 336,4. 4. Montrer que cette suite n'est ni arithmétique, ni géométrique. un+1 - un =0,2 un -50. un+1 - un n'est pas égale à une constaante : la suite n'est pas arithmétique. un+1 / un =0,2 -50 / un. un+1 / un n'est pas constante : la suite n'est pas géométrique. 5. Si on exécute l'algorithme ci-dessous, à la fin k = 9. Comment peut-on interpréter ce résultat ? u = 300 k=0 while u < 500 u=u*1,2u-50 k=k+1. k = 9 ( année 2008), le chiffre d'affaires dépasse 500 000 €.

menu