Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujets 13
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
Une urne contient 150 jetons rouges et 50 jetons bleus, tous
indiscernables au toucher. 20 % des jetons rouges sont gagnants et 40 %
des jetons bleus sont gagnants. Un joueur tire au hasard un jeton de
l’urne.
1. Soit a, b et c trois réels tels que a non nul et soit g la fonction définie sur R par :
g(x) = ax2 +bx+c..
Soit Δ son discriminant.
La représentation graphique de la fonction g dans un repère orthonormé est donnée.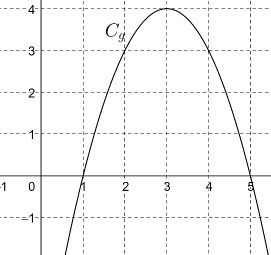
Alors on peut affirmer que :
a. a > 0 et Δ > 0
b. a > 0 et Δ < 0
c. a < 0 et 𝛥 > 0 vrai.
d. a < 0 et Δ < 0.
La parabole coupe l'axe des abscisses en deux points, donc D >0.
La prabole présente un maximum, donc a <0.
2.On considère la fonction f dont la fonction dérivée est la fonction g considérée dans la question 1.
Le tableau des variations de f est :
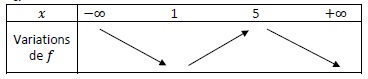
Réponse c.
3.
On considère à nouveau la fonction f dont la fonction dérivée est la
fonction g considérée dans la question 1. On sait de plus que f(3)=7.
La tangente à la courbe représentative de f au point d'abscisse 3 a pour équation réduite :
a. y=4 ; b. y=4x+3 ; c. y=4x+7 ; d. y=4𝑥−5 vrai.
Coefficient directeur de la tangente en x = 3 : f(3) = 4.
Equation réduite de la tangente : y = 4 x+b.
La tangente passe par le point de coordonnées (3 ; 7) : 7 =12+b ; b = -5.
y = 4x-5.
4. Dans
un repère orthonormé, on considère les points A(5;−1),B(3;2) et
C(1;−3). Une équation cartésienne de la droite perpendiculaire à (AB)
et passant par C est :
a. −2x+3y+11=0 vrai ; b. 3x−2y−9=0 ; c. x−3y−10=0 ; d. 3x+2y+3=0.
Coordonnées d'un vecteur directeur de la droite (AB) :(xB-xA ; yB-yA) soit (-2 ; 3).
C'est un vecteur normal à la droite perpendiculaire à la droite (AB).
Equation cartésienne de la droite perpendiculaire à (AB) : -2x+3y+c=0.
C appartient à cette droite :-2 +3*(-3)+c = 0 ; c =11.
5. Dans un repère orthonormé, on considère les points A(5;−1),B(3;2) et C(1;−3).
Une mesure, arrondie au degré, de l’angle ABC est :
a. 11 ; b. 25 ; c. 55 vrai ; d. 88.
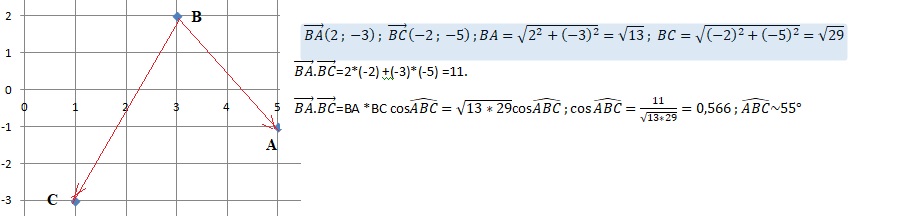
.
Sujet 14.
1. L’inéquation x2+x+2>0 :
a. n’a pas de solution ; b. a une seule solution ; c. a pour ensemble de solution l’intervalle [1 ; 2]
d. a pour solution l’ensemble des nombres réels , vrai.
x2+x+2 =0 ; discriminant D =12-4*2=-7.
Cette équation n'a pas de racines réelles. La parabole ne coupe pas l'axe des abscisses..
Le coefficient a = 1 est positif.
2. Soient les deux vecteurs suivants.
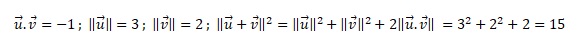
réponse c.
3. Soient A et B deux événements d’un univers tels que PA(B)=0,2 et P(A)=0,5.
Alors la probabilité P(𝐴∩𝐵) est égale à :
a. 0,4 ; b. 0,1 vrai ; c. 0,25 ; d. 0,7.
PA(B)=P(𝐴∩𝐵) / P(A) ;P(𝐴∩𝐵) =0,2 x0,5 = 0,1.
4. Soit (un) une suite arithmétique de terme initial u0= 2 et de raison 3.
La somme S définie par S=u0 + u1 + … + u12 est égale à :
a. 45 ; b. 222 ; c. 260 vrai; d. 301.
u12 = u0 +12r =2+12*3=38
S = nombre de termes x (premier terme + dernier terme) /2 =13(2+38)/2=260.
5. Soit f la fonction définie sur l’ensemble des nombres réels par f(x)=(2x−5)3.
Une expression de la dérivée de f est :
a. 3(2𝑥−5)2 ; b. 6(2𝑥−5)2 vrai; c. 2(2𝑥−5)2 ; d. 23.
On pose u = 2x-5 ; u' =2.
Dérivée de u3 : 3u2 u' =6(2x-5)2.
|
|
Exercice 2. ( 5
points) Sujet 13. En
2000, la production mondiale de plastique était de 187 millions de
tonnes. On suppose que depuis 2000, cette production augmente de 3,7 %
chaque année.
On modélise la production mondiale de plastique, en millions de tonnes,
produite en l’année (2000+n) par la suite de terme général un où n désigne le nombre d’année à partir de l’an 2000.
Ainsi, u0=187.
1. Montrer que la suite (un) est une suite géométrique dont on donnera la raison.
un+1 = 1,037 un, suite géométrique de raison 1,037 et de premier terme 187.
2. Pour tout n entier naturel, exprimer un en fonction de n.
un = 187 x 1,037n.
3. Étudier le sens de variation de la suite (un).
un+1-un =187 x1,037n+1- 187 x1,037n= 187 x1,037n ( 1,037-1) =0,037 x187 x1,037n , positif.
un+1 > un , la suite est croissante.
4. Selon cette estimation, calculer la production mondiale de plastique en 2019. Arrondir au million de tonnes.
u19 = 187 x1,03719 ~373 millions de tonnes.
5. Des études
montrent que 20 % de la quantité totale de plastique se retrouve dans
les océans, et que 70 % de ces déchets finissent par couler.
Montrer que la quantité totale, arrondie au million de tonnes, de
déchets flottants sur l'océan dus à la production de plastique de 2000
à 2019 compris est de 324 millions de tonnes.
Somme des 19 premiers termes de la suite : S = 187(1-1,03720) / (1-1,037) =5398 millions de tonnes.
0,20 x5398 =1080 millions de tonnes dans les océans dont 1080 x0,3=324 millions de tonnes flottent.
Sujet 14.
La courbe ci dessous représente dans un repère du plan une fonction f définie et dérivable sur l’ensemble des nombres réels.
Les points G(2 ; 5) et H (0 ; 1) appartiennent à la courbe
représentative de la fonction f et les tangentes à la courbe aux points
G et H sont horizontales.
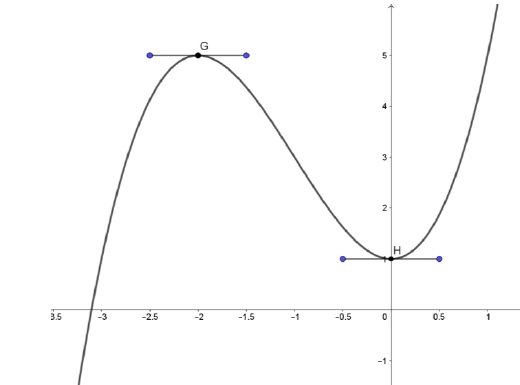
1. Déterminer f(0), f(−2), f ′(0) et f ′(−2).
f(0) =1 ; f(-2) = 5 ; f '(0) =0 ; f '(-2) =0.
2. On admet que pour tout réel x, f(x) peut s’écrire sous la forme :
f(x) = ax3 +bx2+cx+d où a, b, c et d désignent des nombres réels
a. Donner une expression de f '(x).
f '(x) = 3ax2 +2bx+c.
b. Déterminer les valeurs des réels c et d.
f '(0) = 0 =c ; f 0) =1 =d.
c. Déterminer deux équations que vérifient les réels a et b.
d. En déduire que f(x) = x3 +3x2+1.
f '(-2) =0=12a-4b ; b =3a.
f(-2) =5= -8a+4b +1 ; 1=-2a+b ou b =1+2a.
1+2a = 3a ; a = 1 et b = 3.
|
|
Exercice 3. ( 5 points).
Sujet 13.
Un cafetier propose à ses clients des cookies au chocolat ou aux
noisettes en s’approvisionnant dans trois boulangeries. Un client prend
un cookie au hasard.
On note :
C l’événement « le cookie est au chocolat »,
N l’événement « le cookie est aux noisettes »,
B1 l’événement « le cookie provient de la boulangerie 1 »,
B2 l’événement « le cookie provient de la boulangerie 2 »
B3 l’événement « le cookie provient de la boulangerie 3 ».
On suppose que :
– la probabilité que le cookie provienne de la boulangerie 1 est de 0,49 ;
– la probabilité que le cookie provienne de la boulangerie 2 est de 0,36 ;
– PB2(C)=0,4 où PB2(C) est la probabilité conditionnelle de 𝐶 sachant B2 ;
– la probabilité que le cookie soit aux noisettes sachant qu’il provient de la troisième boulangerie est de 0,3.
L’arbre pondéré ci-dessous correspond à la situation et donne une information supplémentaire : le nombre 0,6 sur la branche de B1 à C.
1. Exprimer par une phrase l’information donnée par le nombre 0,6 sur la branche de B1 à C.
La probabilité que le cookies soit au chocolat sachant qu'il provient de la boulangerie 1 est égale à 0,60.
2. Recopier et compléter sur la copie l’arbre pondéré ci-dessous.
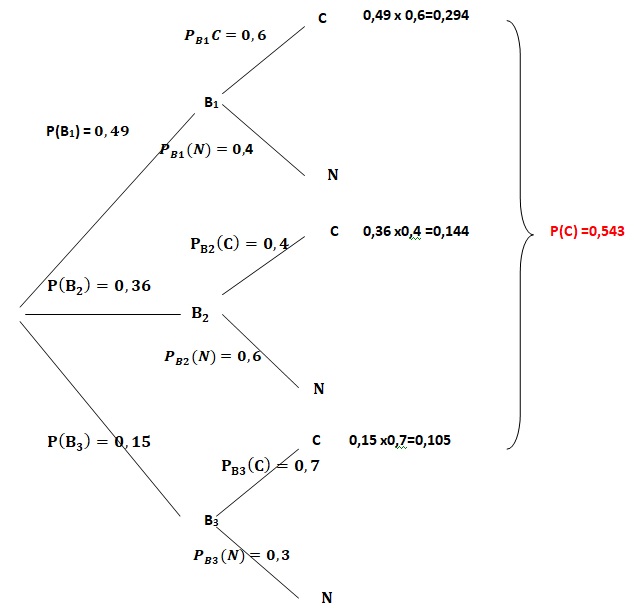
3. Définir par une phrase l’événement 𝐵1∩𝐶 et calculer sa probabilité.
Le cookie est au chocolat et il provient de la boulangerie B1.
P(𝐵1∩𝐶) =0,49 x0,6 =0,294.
4. Montrer la probabilité 𝑃(𝐶) d’avoir un cookie au chocolat est
égale à 0,543.
5. Calculer la probabilité d’avoir un cookie provenant
de la boulangerie 2 sachant qu’il est au chocolat. On donnera le
résultat arrondi au millième.
PC(B2) =P(C n B2) / P(C) =0,144 / 0,543 =0,265.
Sujet 14.
Dans une usine, un four cuit des céramiques à la température de 1 000°C.
À la fin de la cuisson, on éteint le four et commence alors la phase de refroidissement.
Pour un nombre entier naturel n, on note Tn la température en degré Celsius du four au bout de n heures écoulées à partir de l’instant où il a été éteint. On a doncT0 = 1 000.
La température Tn est calculée grâce à l’algorithme suivant :
T ← 1 000
Pour i allant de 1 à n
T←0,82 xT+3,6
Fin pour
1. Quelle est la température du four après une heure de refroidissement ?
T1 =0,82 x1000 +3,6 = 823,6 °.
2. Exprimer Tn+1en fonction de Tn.
Tn+1 = 0,82 Tn +3,6.
3. Déterminer la température du four arrondie à l’unité après 4 heures de refroidissement.
T2 = 0,82 x 823,6 +3,6 =678,952°.
T3 = 0,82 x 678,952 +3,6 =560,34°.
T4 = 0,82 x 560,34 +3,6 ~463°.
4. La porte du four
peut être ouverte sans risque pour les céramiques dès que sa
température est inférieure à 70°C. Afin de déterminer le nombre
d’heures au bout duquel le four peut être ouvert sans risque, on
définit une fonction « froid » en langage Python. Recopier et compléter les instructions manquantes.
def froid() :
T=1000
n=0
while T > 70
T= T*0,82 +3,6
n=n+1
return n
5. Déterminer le nombre d’heures au bout duquel le four peut être ouvert sans risque pour les céramiques.
Tn+1 = 0,82 Tn +3,6 < 70.
T5 = 0,82 x 463 +3,6 ~383° ; T6 = 0,82 x 383 +3,6 ~318° ;T7 = 0,82 x 318 +3,6 ~264° ; T8 = 0,82 x 264 +3,6 ~220° ;
T9 = 0,82 x 220 +3,6 ~184° ;T10 = 0,82 x 184 +3,6 ~155° ;T11 = 0,82 x 463 +3,6 ~130° ;T12 = 0,82 x 130 +3,6 ~110° ;
T13 = 0,82 x 110 +3,6 ~94° ;T14 = 0,82 x 94 +3,6 ~81° ;T15 = 0,82 x 81 +3,6 ~69,7°.
Au bout de 15 heures, on peut ouvrir le four.
|
|
Exercice4. ( 5 points) Sujet 13. 1. Étudier le signe de la fonction P définie sur 𝐑 par P(x) = x2 +4x+3.
x2 +4x+3=0 ; déterminant : D = 42-4*3 = 4 = (2)2.
Solutions :( -4+2) / 2 = -1.
x2 +4x+3 < 0 si x appartient à ]-3; -1[ .
x2 +4x+3 >0 si x appartient à ]-oo ; -3[ union ]-1 ; +oo[.
On considère la fonction f définie sur l’intervalle ]−2;+∞[ par f(x) = (x2 +x-1) / (x+2). et on note Cf sa courbe représentative dans un repère orthogonal du plan. On admet que la fonction 𝑓 est dérivable sur l’intervalle ]−2;+∞[.
2. Montrer que pour tout réel x de l’intervalle ]−2;+∞[, f '(x) = P(x) / (x+2)2 où f ′ est la fonction dérivée de f.
On pose u =x2+x-1 et v = x+2 ; u' =2x+1 ; v' =1.
(u'v-v'u) / v2 =[(2x+1)(x+2)-(x2+x-1)] /(x+2)2 =(2x2+4x+x+2-x2-x+1)(x+2)2 =(x2+4x+3) / (x+2)2 =P(x) / (x+2)2 .
3. Étudier le signe de f '(x) sur ]−2;+∞[ et construire le tableau de variations de la fonction fsur ]−2;+∞[.
(x+2)2 est toujours positif.
f '(x) < 0 si x appartient à :]-2 ; -1[ et f est décroissante.
f '(x) > 0 si x appartient à :]-1 ; +oo[ et f est croissante.
f '(x)=0 si x = -1 et f admet un minimum
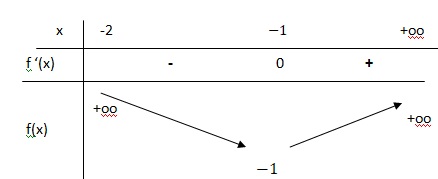
4. Donner le minimum de la fonction f sur ]−2;+∞[ et la valeur pour laquelle il est atteint (on donnera les valeurs exactes).
5. Déterminer le coefficient directeur de la tangente T à la courbe Cf au point d’abscisse 2.
Coefficient directeur de la tangente : f '(2) =15 / 16.
Equation réduite de T : y = 15 /16 x+b.
Le point de coordonnées (2 ; f(2) =1,25= 5 /4) appartient à T.
5 /4 =15 *2 / 16 +b ; b =5 /4 -15 /8 = 10 /8 -15 /8 = -5 /8.
y = 15 /16 x -5 /8.
|
Sujet 14.
Le plan est rapporté à un repère orthonormé.
On considère les points A( -3 ; 1), B(3 ; 5) et C(7 ; 1) dans ce repère.
Le but de cet exercice est de déterminer les coordonnées du centre du
cercle circonscrit au triangle ABC et le rayon de ce cercle.
On rappelle que le cercle circonscrit à un triangle est le cercle passant par les trois sommets de ce triangle.
1. Placer les points A, B et C dans le plan puis construire le cercle circonscrit au triangle ABC.
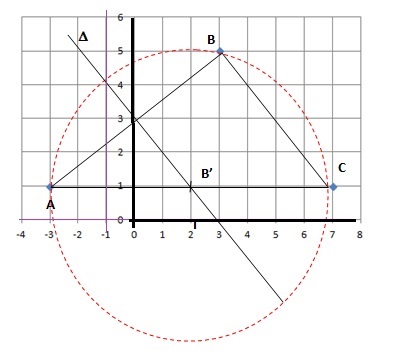
2. Vérifier que la droite Δ d’équation 3x+2y−6=0 est la médiatrice du segment [AB].
Coordonnées du milieu de [AB] : (-3+3) / 2 ; (1+5) / 2 soit (0 ; 3).
3*0+2*3-6=0. Le point milieu de [AB] appartient à D.
Coordonnées d'un vecteur normal de D : (3 ; 2).
Coordonnées d'un vecteur directeur de la droite (AB) :(3 ; 2).
Donc la droite Δ d’équation 3x+2y−6=0 est la médiatrice du segment [AB].
3. Déterminer les coordonnées du point B', milieu du segment [AC].
(xA+xC) / 2 ; yA +yC) / 2 soit B' (2 ; 1)
4. Déterminer les coordonnées du point I, centre du cercle circonscrit au triangle ABC.
Le centre I du cercle circonscrit au triangle ABC est situé sur la médiatrice du côté AC.
AC étant horizontal, la médiatrice est verticale : donc xI = xB' = 2.
IB2 =(3-2)2 +(5-yI)2 = 1+ (5-yI)2; IA2 =(-3-2)2 +(1-yI)2 =25 +(1-yI)2 .
IB2 = IA2 ; 1+ (5-yI)2 =25 +(1-yI)2.
1+25+yI2-10yI =25+1+yI2-2yI ;-10yI =-2yI ;yI =0 ; I(2 ; 0).
5. Calculer une valeur exacte du rayon du cercle circonscrit au triangle ABC.
IA2 =(-3-2)2 +(1-0)2 =25 +1=26 ; IA = 26½.
|
|