Math�matiques.
E3C, contr�le continu premi�re technologique
02 / 2020.
Suite, fonctions, d�riv�e, probabilit�s.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicit�s adapt�es � vos centres
d’int�r�ts.
|
|
.
.....
|
Exercice 2.
Un
restaurateur a produit 2500 kg de d�chets non recyclabless en 2017 et
2350 kg en 2018.
1. D�terminer le
pourcentage de r�duction de la masse de d�chets non recyclables entre
2017 et 2018.
(2500- 2350) / 2500 x100 = 6 %.
2. A partir de
2018, le restaurateur pr�voit de r�duire de 5 % en masse, chaque
ann�e, la masse de ces d�chets. Pour tout entier n, on mod�lise
la masse, exprim�e en kg, de d�chets non recyclables pour l'ann�e 2018
+n � l'aide d'une suite not�e (D).
Ainsi D0 = 2350.
a. Calculer D1
puis D2.
100-5 = 95 ; coefficient multiplicateur 0,95.
D1 = 0,95 D0 = 0,95 x2350 = 2232,5.
D2
= 0,95 D2 = 0,95 x2232,5 = 2120,875.
b. On admet que la
suite est g�om�trique. Donner sa raison.
0,95.
3. On admet que Dn
= 2350 x0,95n.
D�terminer la masse de d�chets non recyclables en 2025.
D7 =2350 x0,957 ~1641 kg.
4. Compl�ter
l'algorithme suivant pour qu'� l& fin de son ex�cution, la variable
D contienne le terme de rang 15 de la suite.
D
= 2350
for n in range(15) :
D = 2350 x0,95
|
.
.
|
Exercice 3.
Une
entreprise produit mensuellement entre 200 et 3000 panneaux solaires.
On mod�lise le r�sultat de l'entreprise r�alis� sur la vente de x
panneaux par la fonction f(x) = -2x2 +90x -400 sur
l'intervalle [2 ; 30].
On
admet que f(x) = -2(x-40)(x-5).
1. Donner le
tableau de signes de la fonction f.
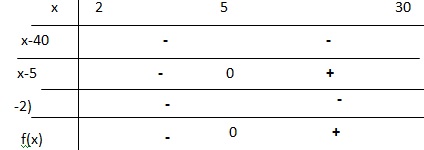
2. A partir de quel
volume de production le r�sultat est-il positif ?
A partir de 500 panneaux le r�sultat est positif.
3. On note f ' la
fonction d�riv�e de la fonction f. Donner l'expression de f '(x).
fonction
|
x2
|
-2x2
|
90x
|
-400
|
f(x)
|
d�riv�e
|
2x
|
-4x
|
90
|
0
|
f
'(x) = -4x +90
|
4. Donner le
tableau de variation de la fonction f.
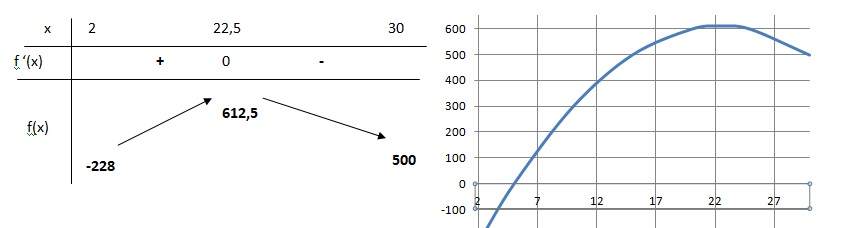
5. D�terminer le
b�n�fice maximal et le volume de production correspondant.
Volume de production : 2250.
B�n�fice maximal : f(22,5) = -2 *22,52 +9*22,5 -400 = 612,5.
|
Exercice 4.
Un g�rant de
restaurant d�veloppe une nouvelle formule de restauration rapide le
midi. Il propose un menu comprenant un plat et un d�sert. Les clients
ont le choix entre deux plats ( viande ou poisson) et trois d�serts (
p�tisserie, laitage ou fruit). Il teste sa formule pendant un mois et
�tudie toutes les commandes pour mieux conna�tre les souhaits de sa
client�le.
Parmi les 600 commandes faites au cours de ce mois, 72 % comprenaient
un plat de viande.
45 % des clients ont pris une p�tisserie et, parmi eux, 44 avaient
choisi le plat de poisson.
Parmi lles 138 commandes comprenant un fruit comme d�sert, 73
comprenaient le plat de poisson.
1. Compl�ter le
tableau suiavnt :
|
P�tisserie
|
laitage
|
fruit
|
total
|
viande
|
270-44=226
|
432-226-65=141
|
138-73=65
|
600
x 0,72 =432
|
poisson
|
44
|
168-44-73=51
|
73
|
600-432=168
|
total
|
600
x0,45 =270
|
600-138-270=192
|
138
|
600
|
On choisit une commande
au hasard et on note :
A l'�v�nement " la commande comprend du poisson".
B l'�v�nement " la commande comprend une p�tisserie".
2. Calculer la
probabilit� de l'�v�nement A.
P(A) = 168 / 600 = 0,28.
3. Calculer la probabilit� de l'�v�nement B.
P(B) = 270 / 600 = 0,45.
4. Calculer la probabilit� que la
commande comprenne � la fois du poisson et une patisserie.
P(A n B)= 44 / 600 ~0,073.
5. Calculer la probabilit� que la
commande comprenne de la viande sachant qu'elle comprend une patisserie.
226 / 270 ~0,84.
|
.
|
|
