Fonctions du second degré et dérivées, mathématiques, classe de première.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
.
..
.....
|
Exercice 1.
Soit la fonction f définie et dérivable sur R telle que : f(x) = 2x2 +2x -3. On note C sa courbe représentative.
1. Déterminer la fonction dérivée f ' de f.
Fonction
|
x2
|
2x2
|
2x
|
-3
|
f(x)
|
Dérivée
|
2x
|
4x
|
2
|
0
|
f '(x) = 4x+2
|
2. Montrer que le coefficient directeur de la tangente à C en x=1 est 6.
f '(1) = 4 *1 +2 = 6.
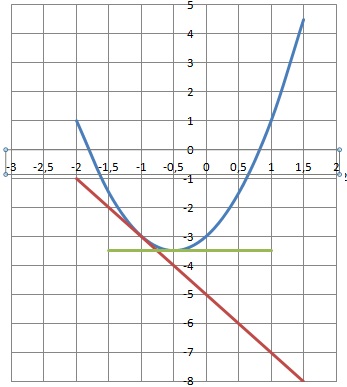
3. Calculer f '(-1) et déterminer l'équation de la tangente à la courbe au point d'abscisse x = -1.
f ' (-1) = 4*(-1)+2) =-4 +2 = -2.
Le coefficient directeur de la droite tangente à la courbe en ce point est égal à -2.
Equation de cette tangente : y = -2x +b.
La tangente passe par le point de coordonnées (-1 ; f(-1)).
f(-1) = 2*(-1)2 +2*(-1) -3 =2-2+3= -3.
-3 = -2 (-1) +b ; -3 = 2 +b ; b = -3-2 = -5.
y = -2x-5.
4. La courbe C admet-elle une ( des) tangente(s) horizontale(s) ? Si oui, quelle est l'équation de cette tangente ?
On cherche la ( les) valeur(s) de x qui annule(nt) la dérivée f '(x).
4 x+2 = 0 ; 4x = -2 ; x = -2 / 4 ; x = -0,5.
La courbe admet une tangente horizontale en x = -0,5.
Equation de cette tangente : y = f(-0,5) = 2 (-0,5)2 +2 *(-0,5) -3 =0,5 -1-3 = -3,5.
|
| ..
... |
.
.
|
Exercice 2.
Soit la fonction f définie et dérivable sur R telle que : f(x) = -2x2 +2x +4. On note C sa courbe représentative.
1. Déterminer la fonction dérivée f ' de f.
Fonction
|
x2
|
-2x2
|
2x
|
+4
|
f(x)
|
Dérivée
|
2x
|
-4x
|
2
|
0
|
f '(x) = -4x+2
|
2. Montrer que le coefficient directeur de la tangente à C en x=1 est -2.
f '(1) = -4 *1 +2 = -2.
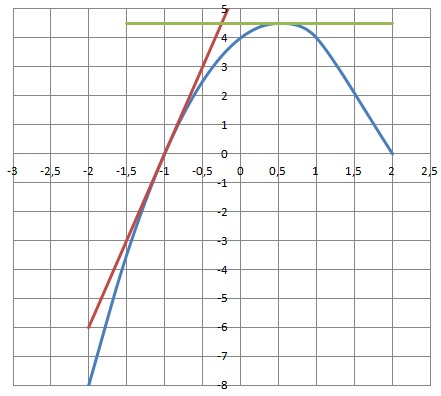
3. Calculer f '(-1) et déterminer l'équation de la tangente à la courbe au point d'abscisse x = -1.
f ' (-1) = -4*(-1)+2) = 4 +2 = 6.
Le coefficient directeur de la droite tangente à la courbe en ce point est égal à 6.
Equation de cette tangente : y = 6x +b.
La tangente passe par le point de coordonnées (-1 ; f(-1)).
f(-1) = -2*(-1)2 +2*(-1) +4 = -2-2+4= 0.
0 = 6 (-1) +b ; 0 = -6 +b ; b = 6.
y =6x+6.
4. La courbe C admet-elle une ( des) tangente(s) horizontale(s) ? Si oui, quelle est l'équation de cette tangente ?
On cherche la ( les) valeur(s) de x qui annule(nt) la dérivée f '(x).
-4 x+2 = 0 ; 4x = 2 ; x = 2 / 4 ; x = 0,5.
La courbe admet une tangente horizontale en x = 0,5.
Equation de cette tangente : y = f(0,5) = 2 (0,5)2 +2 *(0,5) +4 =0,5 +1+4 =4,5.
|
. .
|
.
|
|

