Mathématiques.
E3C, contrôle continu première technologique
02 / 2020.
Fonctions, dérivée, loi de probabilités.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
.
.
|
.
.....
|
Exercice 2.
On
considère la fonction f du second degré définie sur R dont la
représentation graphique est donnée ci-dessous.
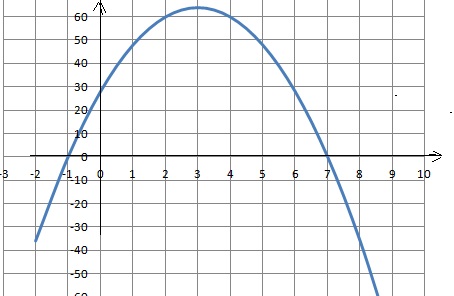
Par lecture graphique, répondre aux questions suivantes.
1. Résoudre dans R
f(x) = 0.
x = -1 ; x = 7.
2. Dresser le
tableau de signe de f(x).
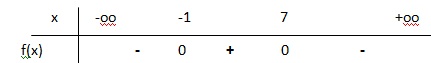
3. Donner une
équation de l'axe de symétrie de la courbe représentative de f(x).
x = 3.
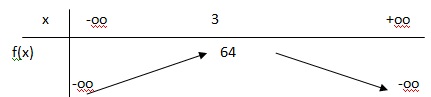
4. Dresser le
tableau de variations de la fonction f.
5. Résoudre dans R
l'inéquation f(x) >
28.
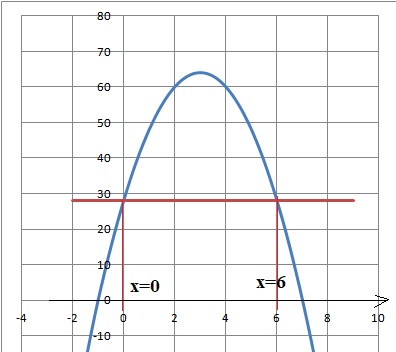
x appartient à [0 ; 6 ].
|
.
.
|
Exercice 3.
Soit la fonction g définie sur R par g(x) =x3-6x2+5.
On a tracé ci-dessous une partie de la représentation graphique
de cette fonction ainsi que la tangente à cette courbe au point
d'abscisse x = 0.
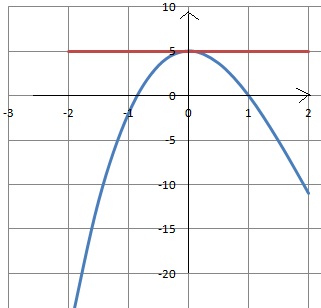
1. Déterminer ghraphiquement le
nombre dérivé de la fonction en x =0.
La tangente à la courbe est horizontale. Le coefficient directeur de la
tangente, donc le nombre dérivé, est nul en x = 0.
2. Déterminer pour
tout réel x, g'(x) ou g'(x) désigne la fonction dérivée de la fonction
g.
fonction
|
x3
|
x2
|
-6x2
|
5
|
dérivée
|
3x2
|
2x
|
-12x
|
0
|
g'(x) = 3x2-12x.
3. 4. On admet que
g'(x) = 3x(x-4).
Dresser le tableau de signe sur R de la fonction g'(x) et en déduire le
tableau de variations de g(x).
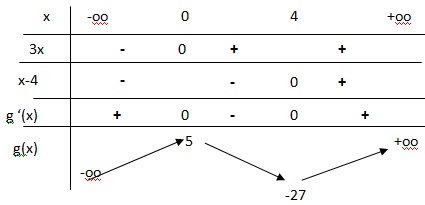
5. On considère
l'algorithme suivant :
x = -1
while x3-6x2+5 > -10
x = x+0,01
Après
exécution x = 1,92. Interpréter ce résultat.
Dès que x devient supérieur à1,92, la fonction g(x) est inférieure à
-10.
Exercice 4.
Dans une maternité, on estime qu'à la naissance, la probabilité qu'un
enfant soit une fille est égale à 0,51. On choisit de manière
indépendante trois enfants nés dans cette maternité. On note X la
variable aléatoire qui prend pour valeur le nombre de filles parmi ces
trois enfants.
1. Représenter
l'expérience aléatoire à l'aide d'un arbre de probabilité.
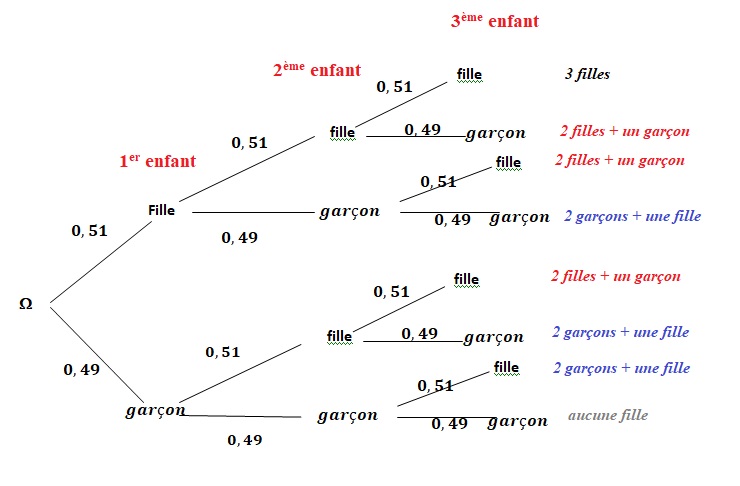
2. Calculer la
probabilité qu'exactement deux enfants soient des filles.
P(X=2) =3 [ 0,51 x0,51 x0,49 ]~0,382.
3. Décrire
l'événement X = 0 et calculer sa probabilité.
Les trois enfants sont des garçons.
P(X=0) = 0,49 x0,49 x0,49 ~0,118.
4. Compléter le
tableau suivant donnant la loi de probabilité de X.
x
|
0
|
1
|
2
|
3
|
P(X
=x)
|
0,118
|
3x0,492
x0,51~0,367
|
0,382
|
0,513
~0,133
|
5. Calculer
l'espérance de cette variable aléatoire et interpréter.
0 x0,118 +1 x0,367 +2 x0,382 +3 x0,133 ~1,53.
Sur 3000 enfants nés dans cette maternité, en moyenne, 1530 sont des
filles.
|
Exercice 5.
L'objectif de cet exercice est de trouver le maximum de la fonction r définie sur l'intervalle [200 ; 400 ] par r(x) = -0,01 x3 +4 x2.
1. On admet que la fonction r est dérivable sur cet intervalle et on note r' sa dérivée.
Calculer r'(x) et montrer que r'(x) = x(-0,03 x +8).
Fonction
|
x3
|
-0,01 x3
|
x2
|
4x2
| r(x)
|
Dérivée
|
3x2
|
-0,03 x2
|
2x
|
8x
| -0,03x2 +8x
|
r'(x) = x(-0,03 x +8).
2.3. Donner le tableau de signe de la fonction r'(x) et en déduire le tableau de variation de la fonction r.
4. Quel est le maximum de cette fonction ? En quelle valeur est-il atteint ?
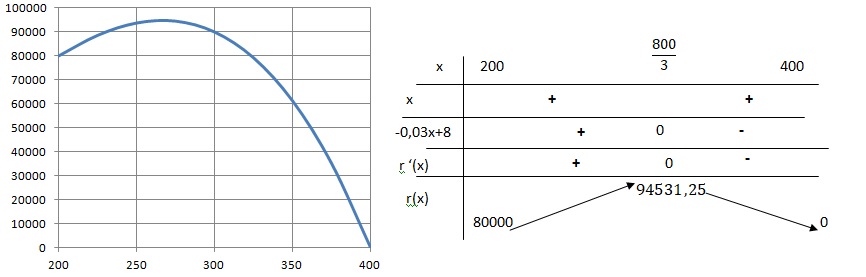
5. Pour vérifier la solution de l'équation r'(x) = 0 sur l'intervalle [200 ; 400 ] on utilise l'algorithme suivant :
def(balayage(pas)
x = 200
while x*(-0,03x*x+8) >0 :
x = x+pas
return (x-pas, x)
Que renvoie l'instruction balayage(1) ?
800 / 3 ~266,7.
Balayage (1) renvoie ( 266 ; 267).
|
.
|
|