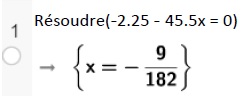Mathématiques.
E3C, contrôle continu première technologique
01 / 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
.
.....
|
Exercice 1.
Sans calculatrice.
1. Donner le coefficient multiplicateur correspondant à une hausse de 25 %.
100 +25 = 125 ; coefficient multiplicateur : 1,25.
2. Donner le coefficient multiplicateur correspondant à une baisse de 11 %.
100 -11 = 89 ; coefficient multiplicateur : 0,89.
3. Une calculatrice qui coûte 79 € bénéficie d'une remise de 20 %. Quel est son prix final ?
100 -20 = 80 ; coefficient multiplicateur : 0,8.
0,8 x79 =63,2 €.
4. Résoudre dans R l'équation : 3x-8 = 5x +10.
3x -5x =10+8 ; -2x = 18 ; x = -18 /2 ; x = -9.
5. Résoudre dans R l'équation : x2 = 144.
Racine carrée (144) = 12 ; x = ±12.
6. Un jean coûte 110 euros, il est d’abord soldé à 30 % puis il est de nouveau soldé à 20 %. Quel est le prix final ?
100-30 =70 ; premier coefficient multiplicateur : 0,70.
110 x0,70 =77.
100-20 = 80 ; second coefficient multiplicateur : 0,80.
77 x0,80 =61,6 €.
7. Résoudre dans R l'inéquation : 5t-6 > 2t+6.
5t-2t >6+6 ; 3t > 12 ; t >12 /3 ; t > 4.
8. Après une augmentation de 20 %, un objet coûte 72 euros. Quel est son prix initial ?
100 +20 = 120 ; coefficient multiplicateur 1,20.
72 / 1,2 = 60 €.
9. A l'aide de la capture d'écran ci-dessous, déterminer le signe sur R de l'expression -2,25 -45,5 x.
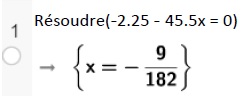
Cette expression est nulle si x = -9 / 182.
Cette expression est négative si x > -9 / 182.
Cette expression est positive si x < -9 / 182.
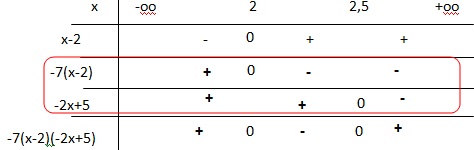
10. Donner le tableau de signe sur R de l’expression − 7(𝑥 − 2)(−2𝑥 + 5).
Exercice
2.
«
En 2017, les Français ont en moyenne produit 513 kg de déchets ménagers
par habitant. » [Source : le site internet Planetescope].
En 2017, le maire d’une commune obtient 530 kg de déchets ménagers en
moyenne par habitant. L’objectif du maire est de réduire la production
de déchets de 1,7 % par an pendant 5 ans, en espérant atteindre la
moyenne nationale de 2017.
On modélise la situation par la suite (d(n))où d(n) représente pour
tout entier naturel n la quantité en kg de déchets ménagers moyenne
produite par habitant de cette ville durant l’année 2017 + n.
1. Justifier que 𝑑(0) = 530 et que pour tout entier naturel n, on a :
d(n+1) = 0,983 x d(n).
La quantité initiale de déchets est de 530 kg par habitant.
100 -1,7 = 98,3 ; coefficient multiplicateur : 0,983.
2. Le tableur nous donne les premières valeurs de la suite et permet de les représenter graphiquement :
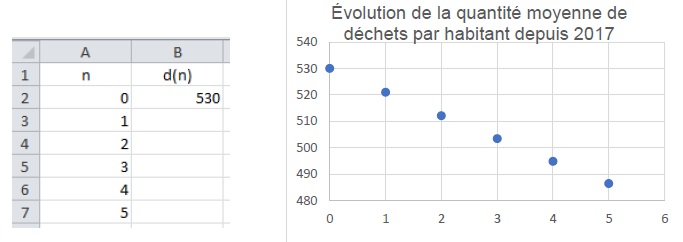
a. Quelle formule destinée à être recopiée vers le bas, peut-on saisir dans la cellule B3 pour obtenir les valeurs de la suite d ?
=B2*0,983
b. Quelle devrait
être à ce rythme-là, la production en kilogramme de déchets ménagers
par habitant dans cette ville en 2022 ? La campagne de sensibilisation
du maire a-t-il permis au maire d’atteindre son objectif ?
2017
|
2018
|
2019
|
2020
|
2021
|
2022
|
530
|
530 x0,983 ~521
|
521 x0,983 ~512
|
512 x0,983 ~503,4
|
503,4 x0,983 ~494,9
|
494,9 x0,983~486,5.
|
486,5 < 513, l'objectif est atteint.
3. Le maire souhaite maintenant atteindre la moyenne européenne de 2017 qui était de 487 kg de déchets ménagers par habitant.
a. Recopier et
compléter l’algorithme ci-dessous permettant d’obtenir le rang de
l’année à partir de laquelle l’objectif du maire sera atteint.
n=0
d = 530
while d > 487
n = n+1
d = 0,983*d
b. En quelle année l’objectif du maire est-il atteint ?
Fin 2022 soit début 2023.
|
.
.
|
Exercice 3 .
Durant une balade en forêt, un enfant se fabrique un arc et des flèches. Il s’intéresse à la trajectoire d’une de ses flèches.
L’enfant décide de tirer sa flèche par-dessus un hangar désaffecté.
La trajectoire est une portion de la courbe représentative de la
fonction f située dans le quart de plan rapporté au repère (O, I, J)
ci-dessous et
définie pour tout réel x, par f(x) = −0,2(x − 5)2 + 6,5.
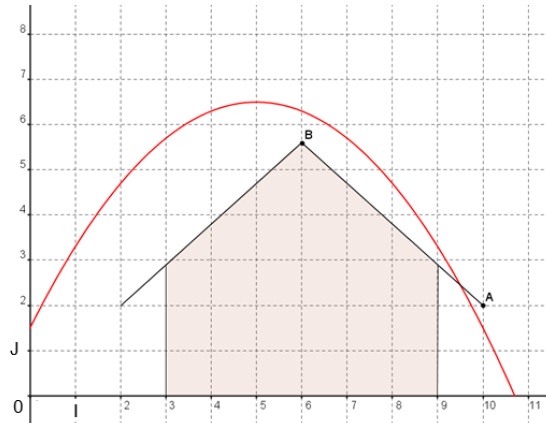
Une unité graphique correspond à 1 mètre dans la réalité.
1. a. De quelle hauteur, en mètre, la flèche est-elle tirée ? Justifier la réponse.
f(0) = −0,2(0 − 5)2 + 6,5= -0,2(-5)2 +6,5 = -5+6,5 = 1,5 m.
b. Quelle hauteur maximale, en mètre, atteint-elle ? Justifier la réponse.
f(5) =−0,2(5 − 5)2 + 6,5= 0+6,5 = 6,5 m.
2. On s’intéresse au pan du toit représenté par le segment [AB], où A(10 ; 2) et B(6 ; 5,6) dans le repère (O, I, J).
Démontrer qu’une équation de la droite (AB) est y = − 0,9x + 11.
Equation de la droite : y = ax+b.
A(10 ; 2) appartient à la droite : 2 =10a +b.
B(6 ; 5,6) appartient à la droite : 5,6 = 6a +b.
Soustraire : 2-5,6 = 10a-6a ; -3,6 = 4 a ; a = -3,6 / 4 = -0,9.
Par suite b = 2-10a = 2-10(0,9) = 2+9=11.
y = -0,9x +11.
On appelle g la fonction affine définie sur R par g(x) = − 0,9 x + 11.
3. Démontrer que pour tout réel x , f(x)-g(x) = − 0,2(x− 5)(x − 9,5).
−0,2(x − 5)2 + 6,5.-(-0,9x+11) =−0,2(x − 5)2 +0,9x+6,5-11=−0,2(x − 5)2 +0,9x -4,5.
−0,2(x − 5)2 +0,9(x-5) = (x-5)[-0,2(x-5)+0,9] =(x-5)(-0,2x+1+0,9) =(x+5)(-0,2x +1,9)
(x+5)(-0,2x +0,2 x9,5) = -0,2(x+5)(x-9,5).
4. Quelles sont les coordonnées exactes du point d’impact sur le toit ?
(x+5)(x-9,5) = 0 avec x positif.
x-9,5 = 0 ; x = 9,5.
y = -0,9 x9,5 +11 =-8,55 +11 = 2,45.
|
..
Exercice 4.
Une
usine d’horlogerie fabrique une série de montres. Au cours de la
fabrication, il apparaît deux types de défauts, le défaut mécanique A
et le défaut esthétique B.
Sur un lot de 200 montres, 2 % des montres fabriquées présentent le
défaut A, 10 % le défaut B et 178 montres ne présentent aucun des deux
défauts.
1. a. Combien de montres fabriquées présentent le défaut A ?
200 x 0,02 = 4.
b. Combien de montres fabriquées présentent le défaut B ?
200 x0,10 = 20.
c. Recopier et compléter sur votre copie le tableau croisé des effectifs suivant :
1. Compléter le tableau suivant :
|
montre avec le défaut A
|
montre sans le défaut A
|
total
|
montre avec le défaut B
|
2
|
18
|
20
|
montre sans le défaut B
|
2
|
178
|
180
|
total
|
4
|
196
|
200
|
2. a. Quelle est la fréquence f des montres présentant les deux défauts ?
2 / 200 = 0,01.
b. Parmi les montres présentant le défaut B, quel est le pourcentage de celles présentant le défaut A ?
2 / 20 = 0,10.
c. Le directeur de l’usine affirme : « Il y a plus de 90 % des montres qui ne présentent aucun des deux défauts ». A-t-il raison ?
178 / 200 =0,89 < 0,90. L'affirmation est fausse.
|
.
|
|