Mathématiques. E3C, contrôle continu première technologique 01 / 2020

Mathématiques. E3C, contrôle continu première technologique 01 / 2020.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.

.....

Exercice 2.
On donne l'évolution de la puissance solaire photovoltaïque dans le monde entre 2008 et 2018.

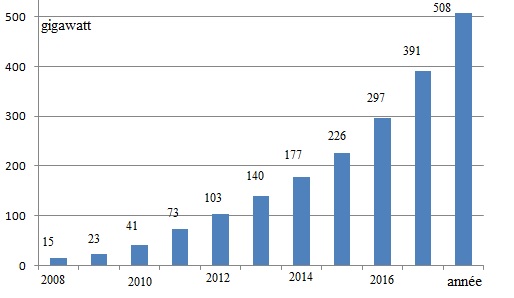
1. Montrer qu'entre fin 2008 et fin 2018, cette puissance solaire a augmenté d'environ 3287 %.
(508-15) / 15 x100 ~3287 %.
2. Calculer les taux d'évolution de cette puissance entre 2016 et 2017, ainsi qu'entre 2017 et 2018.
(391-297) / 297 ~0,32 ( 32 %).
(508-391) / 391 ~0,30 ( 30 %).
3. Pour les années à venir, on fait l'hypothèse que cette puissance va croître de 30 % chaque année.
On note P_n la puissance solaire en l'an 2018 +n.
a. Justifier que P_n+1=1,3 P_n.
100 +30 = 130 % ; coefficient multiplicateur 1,3.
b. Quelle est la nature de la suite P_n ?
P_n+1/ P_n = 1,3, suite géométrique de raison 1,3.
c. Un chercheur affirme que si le taux de croissance se maintient à 30 %, la production dépassera 2400 GW avant fin 2024. A t-il raison ? Justifier.

2018
2019
2020
2021
2022
2023
2024

508
508 x1,3 =660,4
660,4 x1,3=858,5
858,5 x1,3 =1116
1451
1886
2452

Il a donc raison.
5. Le chercheur aimerait savoir en quelle année cette puissance dépasserait 10 000 GW si ce taux de croissance se maintient.
Compléter le script suivant :
p =508
a = 2018
while p <10 000
p = 1,3 * p
a = a+1
print (a).

.
.

. .

Exercice 3 .
Un mobile se déplace sur une droite ghraduée en mètres. Son abscisse p(t) sur cette droite ( exprimée en mètre) en fonction du temps t( minute) depuis le départ est donnée par : p(t) = 0,25 t² -t-3.
1. Quelle est la position du mobile à la date t =0 et à la date t = 2 minutes ?
p(0) = -3 ; p(2) =0,25 x2² -2-3 = -4.
C(40) = 0,25 x40² +500 =900.
2. On donne la courbe représentative de p(t).

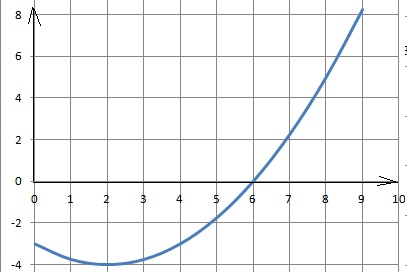
a. Déterminer à quel(s) instant(s) le mobile est à la position -3.
t =0 et t = 4 minutes.
b. Quelle est la vitesse moyenne ( m / min) du mobile entre les instants t = 6 et t = 8 min ?
Distance parcourue : 5-0 = 5 m.
Vitesse moyenne : distance (m) / durée (min) = 5 / 2 = 2,5 m /min.
3.a. Montrer que pour t > 0, p(t) = 0,25(t-6)(t+2).
On développe : (0,25t -1,5)(t+2) =0,25t²+0,5t -1,5t-3=0,25 t² -t-3.
3.b. A l'aide d'un taableau de signes de p sur [0 ; +oo[, déterminer à quels instants le mobile a une abscisse positive ou nulle.

t > 6.

Exercice 4.
On s'interesse à la vente de deux articles particuliers lors d'une promotion. Une meuleuse et une scie sauteuse.
Une enquète réalisée sur 300 clienbts montre que :
63 des clients ont acheté une meuleuse.
80 clients ont acheté une scie sauteuse.
5 % des clients ayant acheté une scie sauteuse ont aussi acheté une meuleuse.
Chaque client a acheté au plus une scie sauteuse et au plus une meuleuse.
1. Compléter le tableau suivant :

achat scie sauteuse
n'achète pas une scie sauteuse
total

achat meuleuse
80 x0,05=4
63-4=59
63

pas d'achat meuleuse
76
161
237

total
80
220 300

2. Quel est le pourcentage de clients ayant acheté une meuleuse ?
63 / 300 = 0,21 (21 %).
3. L'affirmation suivante est-elle vraie ? " au moins 2 % des clients ont acheté les deux outils ". Justifier.
80 x0,05 = 4 ; 4 / 300 =0,013 (1,3 %). L'affirmation est fausse.
4. On choisit au hasard un client : On note les événements suivants :
M "le client achète une meuleuse"
S " le client achète un e scie sauteuse".
a. Calculer P_M(S).
P(M n S) =4 / 300 ; P(M) = 63 / 300 ; P_M(S)= P(M n S) / P(M) =4 / 63 ~0,0635.
b. Calculer P(non S n M).
P(non S n M)=59 / 300 = 0,197.

.

menu