Mathématiques.
E3C, contrôle continu première technologique
01 / 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
.
.....
|
Exercice
2.
Pour
se nourrir un oiseau plonge dans la mer depuis le haut d'une falaise
d'une hauteur de 5 m. La trajectoire de l'oiseau est modélisée par une
fonction h tracée sur l'intervalle [0 ; 6]. L'axe des abscisses
représente le niveau de la mer et l'axe des ordonnées représente la
falaise.
h(x) représente l'altitude en mètre de l'oiseau et x désigne la distance en mètre qui le sépare de la falaise.
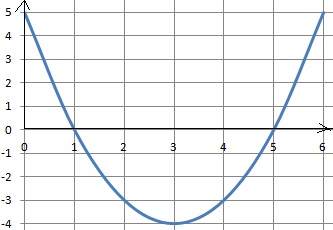
A partir du graphe :
1. Quelle est l'image de 0 par h ? Interpréter.
h(0) = 5 m. Initialement, l'oiseau est sur la falaise, 5 m au dessus du niveau de la mer.
2. A quelles distances de la falaise se trouve l'oiseau lorsqu'il est à une profondeur de 3 m sous la mer ?
2 et 4 m.
La fonction h est définie par h(x) = x2 -6x+5.
3. Montrer que h(x) = (x-1)(x-5).
On développe :h(x) = x2 -5x-x+5 =x2 -6x+5.
4. En déduire le tableau de signe de la fonction h.
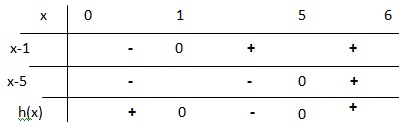
5. Résoudre l'inéquation h(x) < 0 et interpréter.
x appartient à ]1 : 5[.
L'oiseau est sous l'eau situé à une distance comprise entre 1 et 5 mètres de la falaise.
|
| .
. |
.
.
|
Exercice 3 .
Un hotel propose trois formule d'hébergement :
nuit avec petit déjeuner.
demi-pension.
pension complète.
Les durées des séjours sont classés en deux catégories :
séjour d'une semaine ou moins.
Séjours de plus d'une semaine.
5000 clients ont fréquenté l'hotel en 2019.
3100 ont séjourné une semaine ou moins.
750 ont séjourné en pension complète.
3500 ont choisi la demi-pension et parmi eux 1050 sont restés plus d'une semaine.
420 ont séjourné en pension complète pendant plus d'une semaine.
1. Combien de clients ont séjourné plus d'une semaine à l'hotel ?
5000 -3100 = 1900.
2. Compléter le tableau ci-dessous :
|
Nuit avec petit déjeuner
|
Demi-pension
|
Pension complète
|
Total
|
Une semaine ou moins
|
320
|
2450
|
330
|
3100
|
Plus d'une semaine
|
430
|
1050
|
420
|
1900
|
Total
|
750
|
3500
|
750
|
5000
|
.
3. Quel pourcentage de clients a séjourné plus d'une semaine ?.
1900 / 5000 x100 =38 %
4. Parmi les clients qui ont séjourné une semaine ou moins, quelle est la proportion de ceux qui ont choisi la demi-pension ?
2450 / 3100 x100 ~79 %.
5. On
interroge au hasard les clients de l'hotel. Quelle est la probabilité
qu'il ait séjourné en pension complète sachant qu'il est resté plus
d'une semaine ?
420 / 750 =0,56.
|
.
.
|
Exercice 4.
Une entreprise possède trois ateliers A, B et C qui produisent des biscuits selon deux recettes : standard et traditionnelle.
L'entreprise produit 2400 biscuits par jour.
L'atelier A produit 60 % des biscuits.
L'atelier B produit 15 % des biscuits.
|
A
|
B
|
C
|
Total
|
Traditionnnelle
|
576
|
60
|
150
|
786
|
Standard
|
1440-576=864
|
360-60=300
|
450
|
1614
|
Total
|
2400 x0,6=1440
|
2400 x0,15=360
|
600
|
2400
|
1. Compléter le tableau.
2. Calculer le pourcentage de la production correspondant aux biscuits de fabrication traditionnelle.
786 / 2400 x100=32,75.
On prélève au hasard un biscuit dans la production. On note les événements :
C : le biscuit est produit par l'atelier C.
T : le biscuit est de fabrication traditionnelle.
3. Calculer la probabilité de l'événement C.
P(C)=600 /2400 =0,25.
4. Calculer P(C n T).
P(C n T) =150 / 600 =0,25.
5. Quelle est la probabilité qu'un biscuit de recette traditionnelle provienne de l'atelier C ?
150 / 2400 =0,0625.
|
.
|
|