Mathématiques. contrôle continu première technologique 20 / 01 / 2020. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . ..... 1. Un sac contient 11 jetons rouges, 3 jetons bleus et 6 jetons verts. Déterminer ( en %) la proportion dejetons verts dans le sac. 6 / (11 +3 +6) = 6 / 20 = 0,3 ( 30 %). 2. 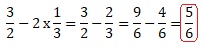Donner le résultat sous forme simplifiée : 3. Développer et réduire : 3x(x-1)+(x+2)2 =3x2-3x+x2+4+4x=4x2+x+4. 4. f est une fonction définie par f(x) =2x2 +3x-5. Calculer l'image de -1 par f. f(-1) = 2(-1)2 +3(-1) -5 = 2-3-5= -6. 5. Donner la forme factorisée de : (2x-3)(x+2)-5(x+2). (x+2)(2x-3-5) =(x+2)(2x-8) = 2(x+2)(x-4). 6. La surface S d'une sphère est donnée par S = 4 p R2. Exprimer R en fonction de S. R2 = S / (4p) ; R = racine carrée (S / (4p) =0,5 racine carrée (S / (p). 7. Calculer en cm3 le volume V d'un cylindre de rayon R = 0,4 cm et de hauteur h = 5 cm en prenant p ~3. Rappel : V = p R2 h. V = 3 x0,42 x5 =2,4 cm3. 8. Déterminer l'équation réduite de la droite (D) passant par les points A(2 ; 4) et B(6 ; 6). y = ax +b. A appartient à la droite : 4 =2a+b ; B appartient à la droite : 6 = 6a +b. Soustraire : 6-4 = 6a-2a+b-b ; 2 = 4a ; a = 0,5. Par suite 4 = 1 +b ; b = 3. y = 0,5x+3. 9 et 10.Résoudre graphiquement f(x) = 0 et f(x) = g(x). 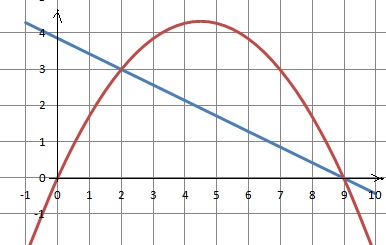f(0) = 0 = f(9) = 0 ; g(9) = f(9)=0 ; f(2) = g(2) = 3. Exercice 2. En 2016, la production de voitures électriques d'un groupe était de 53 000 véhicules. En 2017 le nombre de véhicules produits a augmenté de 5 %.  La direction décide de maintenir cette progression chaque année. 1. Déterminer le nombre de véhicules produits en 2017. 100 +5 = 105 ; corfficient directeut1,05. 53 000 x1,05 =55 650. On modélise le nombre de véhicules produits en 2016 +n par la suite (vn). 2.  Exprimer vn+1 en fonction de vn. Quelle est la nature de cette suite ? vn+1 = 1,05 vn, suite géométrique. 3. On souhaite déterminer l'année au cours de laquelle la production de véhicules électriques aura doublé par rapport à la production 2016. On considère le programme ci-dessous. Compléter ce programme. v = 53 000 a = 2016 while v <106 000 v = 1,05 * v a = a+1 print (a) Donner une réponse à l'aide de la calculatrice. 2016 +15 = 2031. . . . . Exercice 3 . Les lycéens ont fabriqué une fusée qui est lancée à partir d'une plate forme située à 8 m de hauteur. La hauteur de la fusée( en mètre) atteinte en fonction du temps ( en dixième de seconde) est modélisée par : f(t) = -0,5 t2 +10 t+8 pour t appartenant à [0 ; 20]. 1. Calculer f(10) et interpréter le résultat. f(10) = -0,5 *102 +10 x10 +8 = -50+100+8=58. La hauteur atteinte par la fusée est de 58 m au bout d'une seconde. 2. L'explosion de la fusée de feu d'artifice ne peut être déclenchée qu'à une hauteur minimale de 40 ùm. Les lycéens cherchent le temps de vol à programmer. On note g(t) = -0,5t2 +10t -32. a. Vérifier que g(t) = -0,5(t-4)(t-16). On développe : (-0,5t +2)(t-16) = -0,5t2+8t+2t-32 =-0,5t2 +10t -32 = g(t). b. Montrer que le problème revient à résoudre g(t) >0. g(t) = f(t) -40. f(t) >  40 ; g(t) > 0. c. Résoudre l'inéquation et rèpondre au problème. t doit être compris entre 4 et 16 dixièmes de secondes.. . .   Exercice 4. Un fabricant d'ampoules possède deux machines A et B. La machine A fournit 65 % de la production. Certaines ampoules présentent un défaut : 8 % à la sortie de la machine A et 4 % à la sortie de la machine B présentent un défaut. On produit 15 000 ampoules par jour. 1. Combien d'ampoules proviennent de chaque machine ? Machine A : 15 000 x0,65 =9 750. Machine B : 15 000-9 750 =5 250. 2. Compléter le tableau suivant : Machine A Machine B  Total Avec défaut 780 5250 x 0,04=210 990 Sans défaut 8970 5040 14 010 Total 9750 5 250 15000 3. Calculer la fréquence en pourcentage des ampoules ayant un défaut. 990 / 15 000 x100 = 6,6 %. 4. On définit les événements : A : " l'ampoule provient de la machine A". D : " l'ampoule présente un défaut". Déterminer A n D. 780 / 15000 =0,052 (5,2 %). Ou bien 0,65 x 0,08 =0,052. .

menu