Probabilités
: contrôle continu première technologique
20 / 01 / 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
.
.....
|
Exercice 1.
Un match de rugby entre deux équipes A et B se déroule dans un stade accueillant 75 000 spectateurs.
52500 supportent l'équipe A.
32250 sont licenciés à la FFR.
13125 supporters de l'équipe A sont licenciés à la FFR..
1. Compléter le tableau suivant :
|
Licencies à la FFR
|
non licencies à la FFR
|
Total
|
Supporter de l'équipe A
|
13 125
|
39 375
|
52 500
|
Supporter de l'équipe B
|
19 125
|
3 375
|
22 500
|
Total
|
32 250
|
42 750
|
75 000
|
2. On interroge au hasard un spectateur et on considère les événements suuivants :
A : " le spectateur est un supporter de l'équipe A".
B : " le spectateur est un supporter de l'équipe B".
L : " le spectateur est licencié à la FFR".
Calculer les probabilités suivantes.
P(B) =22 500 / 75 000 = 0,3.
Décrire l'événement A n L.
Le spectateur est licencié à la FFR et supporte l'équipe A.
Calculer P(A n L).
P(A n L) = 13 125 / 75000 =0,175.
3. On interroge au hasard un spectateur. C'est un supporter de l'équipe B. Calculer la probabilité qu'il soit licencié à la FFR.
19 125 / 22 500 =0,85.
Exercice 2.
Dans
un club multisport de 400 adhérents, le tennis, le squash et le
badminton sont pratiqués. Les adhérents sont classés suivant leurs
catégories : enfant; senior, vétéran.
15 % pratiquent le badmington et parmi ceux-là, le tiers sont des enfants.
75 % pratiquent le tennis et parmi eux, 32 % sont des seniors.
Parmi les adhérents pratiquant le squash, aucun n'est enfant et 20 sont des vétérans.
1. Compléter le tableau suivant :
|
Badminton
|
Tennis
|
Squash
|
Total
|
Enfant
|
20
|
130
|
0
|
150
|
Senior
|
30
|
96
|
20
|
146
|
Vétéran
|
10
|
74
|
20
|
104
|
Total
|
60
|
300
|
40
|
400
|
Dans les questions suivantes, les résultats seront donnés sous forme de fractions irréductibles.
2. On choisit au hasard un adhérent parmi les 400 adhérents du club.
On considère les événements suivants :
E : " l'adhérent est un enfant".
S : " l'adhérent est un senior".
V: "l'adhérent est un senior".
T :" l'adhérent joue au tennis".
D : " l'adhérent joue au squash".
B : " l'adhérent joue au badminton".
a. Déterminer la probabilité des événements S et T.
P(S) = 146 / 400 =73 / 200.
P(T) = 300 / 400 = 3 / 4.
b. Décrire à l'aide d'une phrase l'événement S n T puis calculer sa probabilité.
L'adhérent est un senior qui joue au tennis.
P(S n T) = 96 / 400 = 24 / 100 =6 /25.
3. On choisit au hasard un adhérent parmi les joueurs de badminton. Calculer la probabilité que ce soit un vétéran.
PB (V) = 10 / 60 = 1 / 6.
4. Calculer la probabilité conditionnelle de E sachant T, notée PT(E).
PT(E) = 130 / 300 = 13 / 30.
|
| ..
... |
.
.
|
Exercice 3 .
Un
sac contient trois boules rouges et deux boules jaunes. Une partie
consiste à prélever deux boules successivement en replaçant la première
boule tirée dans l'urne avant le second tirage.
On considère les événements suivants :
R : " la boule tirée est rouge".
S : "la boule tirée est jaune".
1. Compléter l'arbre de probabilités suivant :
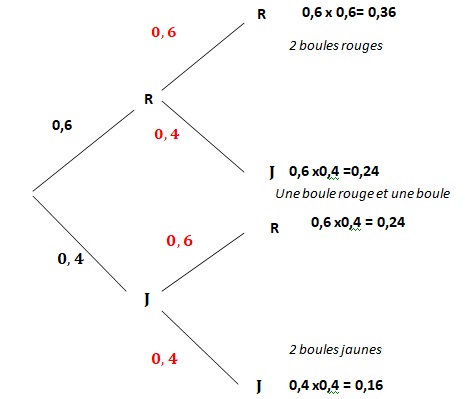
Chaque boule rouge tirée rapporte 2 € et chaque boule jaune tirée fait perdre 1 €.
Soi X la variable aléatoire égale au gain à l'issue de la partie.
2. Compléter le tableau suivant :
k
|
-2
|
1
|
4
|
P(X=k)
|
0,16
|
0,48
|
0,36
|
Bilan ( gain ou perte)
|
-2 x0,16) = -0,32
|
1 x0,48 = 0,48
|
4 x0,36 =1,44
|
3. Déterminer P(X >0). Interpréter ce résultat.
P(X >0) =0,48 +0,36 =0,84.
La probabilité de gagner est égale à 0,84.
4. Calculer l'espérance E(X) et interpréter.
E(X) = -2 x0,16 +1 x0,48 +4 x0,36 =1,6.
En jouant un grand nombre de parties, on gagne en moyenne 1,6 € par partie.
|
.
.
|
Exercice 4.
Un
fabricant d'ampoules possède deux machines A et B. La machine A fournit
65 % de la production. Certaines ampoules présentent un défaut :
8 % à la sortie de la machine A et 4 % à la sortie de la machine B
présentent un défaut.
On produit 15 000 ampoules par jour.
1. Combien d'ampoules proviennent de chaque machine ?
Machine A : 15 000 x0,65 =9 750.
Machine B : 15 000-9 750 =5 250.
2. Compléter le tableau suivant :
|
Machine
A
|
Machine
B
|
Total
|
Avec
défaut
|
780
|
5250 x 0,04=210
|
990
|
Sans
défaut
|
8970
|
5040
|
14 010
|
Total
|
9750
|
5 250
|
15000
|
3. Calculer la fréquence en pourcentage
des ampoules ayant un défaut.
990 / 15 000 x100 = 6,6 %.
4. On définit les événements :
A : " l'ampoule provient de la machine A".
D : " l'ampoule présente un défaut".
Déterminer A n D.
780 / 15000 =0,052 (5,2 %).
Ou bien 0,65 x 0,08 =0,052.
|
.
|
|