Mathématiques : contrôle continu première technologique 20 / 01 / 2020

Mathématiques : contrôle continu première technologique 20 / 01 / 2020.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.

.....

Exercice2. 5 points.
Un responsable commercial du service vélo à assistance électrique ( VAE) doit proposer une estimation du nombre de vélos à produire pour les années à venir. En 2018 l'entreprise a réalisé 4500 ventes de VAE. Ce responsable estime que le nombre de ventes progressera de 22 % chaque année.
On note v_n le nombre de VAE vendu par l'entreprise en 2018 +n. Ainsi v₀ = 4500.
1. Compléter la troisième ligne du tableau suivant :

A
B
C
D
E

1
Rang de l'année n
0
1
2
3

2
Nombre de ventes v_n
4500
4500 x1,22 =5490
5490x1,22=6698
6698 x1,22=8171

2. Exprimer v_n+1 en fonction de v_n.
100 +22 = 122 ; coefficient multiplicateur 1,22..
v_n+1 = 1,22 v_n.
3. Donner la nature de la suite en précisant sa raison.
v_n+1 / v_n = 1,22. Suite géométrique.
4. Le responsable souhaite connaître le nombre d'années nécessaire pour que les ventes de VAE dépassent 20 000 unités. Il a préparé un script en langage python. Compléter ce script donnant la réponse au problème.
def temps_attente()
v = 4500
n = 0
while v < 20 000 :
v = v * 1,22
n=n+1
return n.
5. Déterminer la valeur renvoyée par ce programme. .

2021
2022 (n=3)
2023(n=4)
2024(n=5) 2025(n=6)
2026 (n=7)

8171
8171 x 1,22 =9 969
9 969 x1,22 =12 162
12 162 x1,22 =14 837
18101
22084

v < 20 000
vrai
vrai
vrai
vrai
Faux

.. ...

. .

Exercice 3 ( 5 points).
Une entreprise commercialise des chocolats. La production hebdomadaire maximale est de 30 000 chocolats. On suppose que la totalité est vendue chaque semaine. les charges de production, en euros, pour x milliers de chocolats vendus sont modélisées par la fonction C définie sur [0 ; 30 ] par C(x) = 4x² +4x+520.
Prix de vente d'un chocolat : 0,128 €.
Pour la vente de x milliers de chocolats le chiffre d'affaires, en euros, est donné par la fonction R définie sur [0 ; 30 ) par R(x) = 128 x.
C_R et C_C désignent les courbes représentatives de R et C.

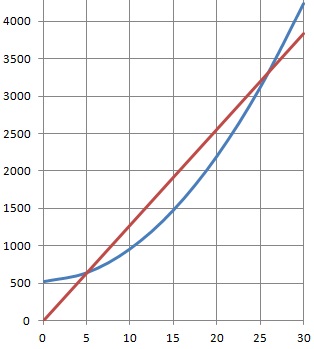
Le résultat réalisé pour x milliers de chocolats vendus est donné par la fonction B par B(x) = R(x) - C(x).
1. Montrer que B(x) = -4x² +124 x -520.
B(x) = 128 x -(4x² +4x+520) = -4x² +124 x -520.
2. Montrer que B(x) = -4(x-5)(x-26).
On développe : -4 ( x² -26x -5x +130)= -4 ( x² -31x +130)= -4x² +124 x -520.
3. En déduire le tableau de signe de B(x).

4. Déterminer les quantités de chocolat à produire pour obtenir un résultat positif.
x doit être compris entre 5000 et 26 000 chocolats , ]5000 ; 26 000 [.
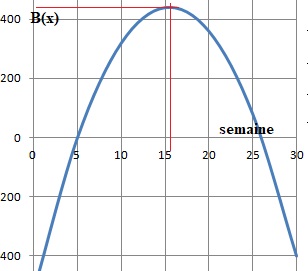
5. Quelle est la quantité de chocolat à produire pour maximiser le bénéfice habdomadaire ? Donner sa valeur.
B(x) = -4x² +124 x -520.
x = -b / (2a) = -124 / (2 *(-4))=124 / 8 =15,5.
B(15,5) = -4 *15,5²+124*15,5 -520= -961 +1922-520=441 €.

.
.

Exercice 4. ( 5 points).
Un sac contient trois boules rouges et deux boules jaunes. Une partie consiste à prélever deux boules successivement en replaçant la première boule tirée dans l'urne avant le second tirage.
On considère les événements suivants :
R : " la boule tirée est rouge".
S : "la boule tirée est jaune".
1. Compléter l'arbre de probabilités suivant :

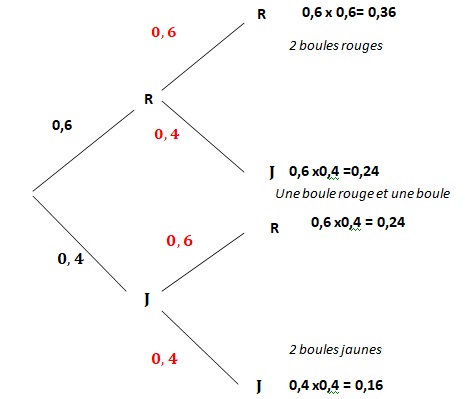
Chaque boule rouge tirée rapporte 2 € et chaque boule jaune tirée fait perdre 1 €.
Soi X la variable aléatoire égale au gain à l'issue de la partie.
2. Compléter le tableau suivant :

k
-2
1
4

P(X=k)
0,16
0,48
0,36

Bilan ( gain ou perte)
-2 x0,16) = -0,32
1 x0,48 = 0,48
4 x0,36 =1,44

3. Déterminer P(X >0). Interpréter ce résultat.
P(X >0) =0,48 +0,36 =0,84.
La probabilité de gagner est égale à 0,84.
4. Calculer l'espérance E(X) et interpréter.
E(X) = -2 x0,16 +1 x0,48 +4 x0,36 =1,6.
En jouant un grand nombre de parties, on gagne en moyenne 1,6 € par partie.

.

menu