Mathématiques,
tableau de variation d'une fonction.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
...
|
....
|
f(x) = x3+7x+24. f '(x) = 3x2 +7.
f '(x) >0 ; f(x) strictement croissante.
f(x) = x-1 /x définie sur R*.
f '(x) =1+1 /x2 =(x2+1) / x2.
f '(x) >0 ; f(x) strictement croissante.
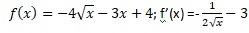 définie sursur R+. définie sursur R+.
f '(x) <0 ; f(x) strictement décroissante.
f(x) = -x3 +1 /x définie sur R*.
f '(x) = -3x2-1/x2 ; f '(x) <0 ; f(x) strictement décroissante.
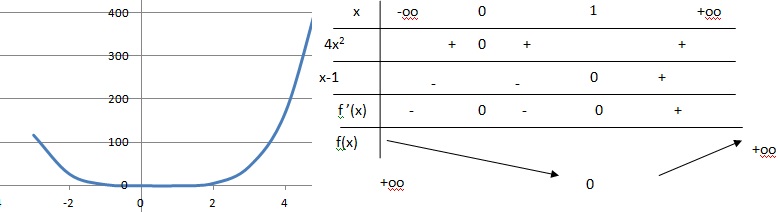
f(x) = x3(x-4 / 3).
On pose u = x3 ; v = x-4 /3.
u' = 3x2 ; v' = 1 ; u'v+v'u = 3x2(x-4 /3) +x3 =4x3 -4x2 = 4x2(x-1).
f(x) = x /(1+x2).
On pose u = x et v = 1+x2 ; u' = 1 ; v' = 2x.
(u'v -v'u) / v2 =(1+x2-2x2) /(1+x2)2=(1-x)(1+x) / (1+x2)2.
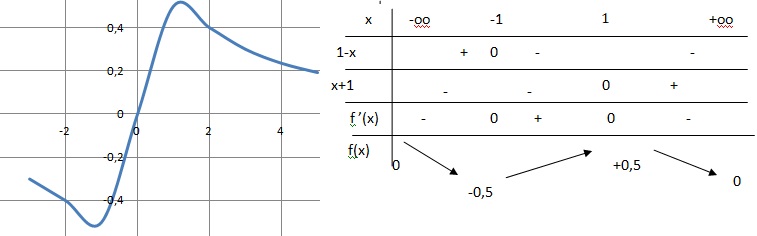
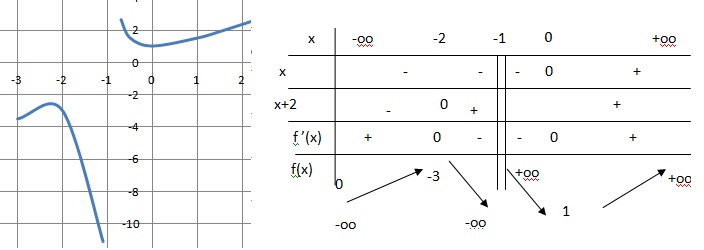
f(x) = (x2+x+1) / (1+x) définie sur -{-1}.
On pose u =x2+x+1 et v = 1+x : u' = 2x+1 ; v' = 1.
(u'v -v'u) / v2 =((1+x)(2x+1)-(x2+x+1)) / (1+x)2.
f '(x) = (1+3x+2x2) /(1+x)2 = x(x+2) / (1+x)2.
f(x) = 1 /(1+racine(x) définie sur R+.
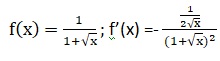
f '(x) >0 ; f(x) strictement décroissante de 1 à plus 0.
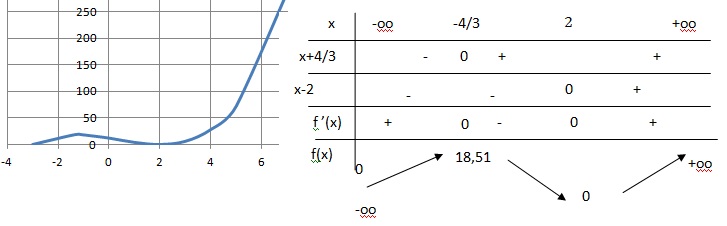
f(x) = x3-x2-8x+12. f '(x) =3x2-2x-8 =(x-2)(x+4/3).
|