Mathématiques,
concours ASTPS Ouest 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
...
.....
|
81. La factorisation de 121x2-49a2b2 donne :
A. 49a2b2 -121x2.
B. 121x2-49ab .
C. 121x2-49a2b2.
D. (11x-7ab)(11x+7ab). Vrai.
82. Le développement de l'expression 4x[3-(7-x)][4x-(x-2)] est :
A. -12x3+40x2+32x.
B. 12x3-40x2-32x. Vrai.
C. 10x4+13x3-12x.
D. -12x3+40x-32.
4x(3-7+x)(4x-x+2) =4x(-4+x)(3x+2) =4x(3x2-10x-8) =12x3-40x2-32x.
83.
On retranche un même nombre au numérateur et au dénominateur de la
fraction 23 / 38. Quel est ce nombre sachant que l'on obtient l'inverse
de la fraction initiale ?
59 ; 61 vrai ; 60 ; 62.
(23-x) / (38-x) = 38 / 23. 23-x = ±38 ; x = -15 ou x = 61.
38-x =± 23 ; x = 15 ou x = 61.
84. Calculer la longueur et la largeur d'un rectangle de périmètre 221m et d'aire 2 226 m2.
A. 80 m et 30 m.
B. 84 m et 26,5 m. Vrai.
C. 86,2 m et 39,5 m.
D. 83,5 m et 24,5.
Longueur + largeur = 221 / 2 =110,5 m.
Longueur fois largeur = 2 226 ; longueur ( 110,5 -longueur) = 2 226.
On note X la longueur : - X2+110,5 X-2 226 =0.
Discriminant D = 110,52 -4 (-1)(-2226) =3306,25 =57,5.
X = (-110,5 -57,5) / (-2) =84.
85. Donner l'écriture la plus simple possible de : racine carrée (18) / racine carrée (2).
A. 2 ; B. racine carrée (6) ; C. 3 vrai. D. 9.
racine carrée ( 18 /2) = racine carrée (9) = 3.
86. Quel est le résultat de B = 9 -3 / (1/3) +1 ?
A. 4 ; B. 2 ; C. 3 ; D. 1. Vrai.
Diviser par 1 /3, c'est multiplier par 3. B = 9-3*3+1=9-9+1 = 1.
87. La masse en gramme d'un électron est : 0,000 000 000 000 000 000 000 000 000 91094. Son écriture scientifique est :
A. 0,91094 10-28 ; B. 0,091094 10-25 ; C. 9,1094 10-32 ; D. 9,1094 10-28. Vrai.
88. Un
triangle a ses côtés qui mesurent x+4 cm, x cm et 9 cm. le côté
mesurant x+4 est le plus long. Pour que ce triangle soit rectangle, x
prend la valeur :
A. 8,13 cm ; B. 8,135 cm ;
C. 8,12 cm ; D. 8,125 cm. Vrai.
(x+4)2 = x2 +92 ; x2+8x+16 -x2=81 ; 8x = 81-16 =65 ; x = 65 / 8 =8,125.
89.
Une entreprise signe un accord salarial prévoyant une augmenntation de
salaire de ses employés de 7,5 % par an pendant 10 ans. Un
employé a un salaire mensuel de 1500 €. Quel sera son salaire mensuel
après trois ans ?
A. 1863,45 € vrai ; B. 1612,50 € ; C. 1743,50 € ; D. 1733,44 €.
Coefficient multiplicateur : 1,075 ; 1500 x 1,0753=1863,45.
90. Ma facture d'eau est passée de 295 € à 212 €. Quelle est sa variation exprimée en pourcentage ?
A. 14,28
; B. 18,24 %. C. -24 %. D.-28,14 % vrai.
(212-295) *100 / 295 = -28,14 .
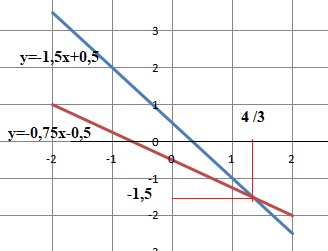
91. Les coordonnées du point d'intersection des droites d'équation y= -1,5x +0,5 et y = -0,75x -0,5 sont :
A. -1/6 ; 4 /9.
B. 4/9 ; -1 /6 .
C. 9 /4 ; -6.
D. 6 ; -9 /4.
-1,5x+0,5 = -0,75x -0,5 ; 0,75x = 1 ; x = 4 /3 ; par suite y = -1,5.
92. On
lance au hasard une flèche dans la cible suivante qui est telle que
ACDF soit un carré et ABEF soit un rectangle. On suppose que toutes les
flèchettes touchent la cible. Quelle est la probabilité que la flèche
tombe dans le reactangle ABEF ?
A. 1 /3 vrai ; B. 3 / 5 ; C. 1 /4 ; D. 2 /6.

Aire du rectangle ABEF = aire du carré ACDF / 3.
93.
On dispose d'un dé à 12 faces numérotées de 1 à 12. On note le numéro
de la fce supérieure du dé. Quelle est la probabilité de ne pas avoir
un multiple de 3 ?
A. 1 /3 ; B. 2 /3 vrai ; C. 3 /4 ; D. 1 /4.
Cas favorables : 1 ; 2 ; 4 ; 5 ; 7 ; 8 ; 10 ; 11 soit 8 sur 12 possibilités.
94.
Le tableau suivant donne la répartition des notes obtenues à un
contrôle par les 27 élèves d'une classe. Quel est le pourcentage
d'élèves ayant eu une note supérieure ou égale à 10.
notes
|
6
|
8
|
10
|
13
|
14
|
17
|
effectifs
|
3
|
5
|
6
|
7
|
5
|
1
|
A. 70,3 % vrai ; B. 67,3 % ;
C. 61,4 % ; D. 69,8 %.
19 / 27 *100 ~70,3 %.
|
.
.
|
95. Le salaire mensuel d'une entreprise de 62 employés se répartissent ainsi :
salaires ( €)
|
effectifs
|
[1000 ; 2000 [
|
50
|
[2000 ; 4000 [
|
10
|
[4000 ; 10 000 [
|
2
|
Quel est le salaire moyen ?
A. 2000,61 ; B. 1920,4
; C. 1919,35 vrai ; D. 1875,19.
(50 x1500 +5 x3000 +7000 x2 ) / 62 =1919,35.
96. Quelle est la médiane de la série suivante :
valeurs
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
Fréquences
|
25
|
3
|
4
|
11
|
8
|
6
|
5
|
7
|
5
|
5
|
6
|
15
|
A. 11 : B. 10 ; C. 12 vrai : D. 13.
La 50è valeur est 12.
97. Quelle est l'écriture décimale de A = 3 x 10-1 -1,2 x10-2.
A. 0,288. Vrai. B. 3,2. C. 0,5. D. 1,45.
A = 0,3 -0,012 =0,288.
98. Donner l'écriiture scientifique de F = (4 x10-3 x15 x102x7x10-4) /(5x108 x196½x103)
A. 1,4 10-12.
B. 1,5 1012.
C. 2 1016.
D. 6 10-16 vrai.
F = (4 x15x7x10-5) / (5x14x1011)=6 x 10-16.
99. Donner le résultat sous la forme an de (-2)5 x165 /(-8)-3.
A. 424 ; B. (-2)34 ; C. 234 vrai ; D. (-4)30.
(-2x16)5 / (-8)-3 =(-2x16)5 x(-8)3 =(2x24)5 x29 =225 x29= 234 .
100. Ecrire sous la forme a * racine carrée (b) : A = 2 *racine carrée (45) +racine carrée(20)-3 * racine carrée(80)
A. -4*racine carrée (5). Vrai.
B. -2*racine carrée (10)
C. 3 *racine carrée (3)
D. 7*racine carrée(5).
A = 2 *racine carrée (32*5) +racine carrée(22*5)-3 * racine carrée(42*5)
A = (6 +2-12) *racine carrée(5) = -4 racine carrée (5).
101. Le volume exact du boudin suivant est de ( en cm3).
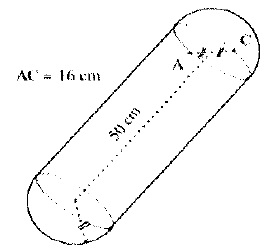
A. 5248 /3 p.
B. 10513 /3 p.
C. 2048 /3 p.
D. 11648 /3 p. Vrai.
Volume d'une sphère de rayon 8 cm + volume d'un cylindre de rayon 8 cm et de hauteur 50 cm.
4 / 3 x83 p+82x 50 p =2048 / 3 p+3200 p =11648 / 3 p.
102. Le volume du parallélépipède rectangle a été multiplié par 27. De combien s'est agrandie son aire ?
A. 9 vrai ; B. 27 ; C. 3 ; D. 18.
Chaque dimension a été multipliée par 3. L'aire a été multipliée par 9.
103.
Roméo R veut rejoindre Juliette J à sa fenètre. Pour cela, il place une
échelle JR . Le mur et le sol sont perpendiculaires. HR = 3 ; JH = 4.
Le cosinus de l'angle HJR est égal à :
A. 5 /4 ; B. 3 /5 ; C.3 /4 ; D. 4 /5 vrai.
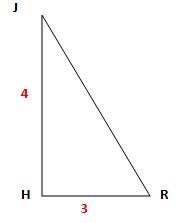
JR2 = 32 +42 = 25 ; JR = 5 ; cos HJR = HJ / JR = 4 / 5.
104.
Un lecteur d'une bibliothèque est passionné de romans policiers et de
bibliographies. Cette bibliothèque lui propose 150 romans policiers et
50 bibliographies. 40 % des écrivains de romans policiers sont français
et 70 % des écrivains bibliographiques sont français. Le lecteur
choisit au hasard un livre parmi les deux cents ouvrages. La
probabilité que le lecteur choisisse un livre d'un écrivain français
est :
A. l0,9 ; B.0,475 vrai ; C. 0,7 ; D. 0,8.
150 /200 x 0,40 +50 / 200 x 0,70 = 0,3 +0,175 = 0,475.
105. A et B sont deux événements indépendants tels que p(A) =0,2 et p(B) =0,3. Alors p( A u B) =
A. 0,06 ; B. 0,44. Vrai ; C. 0,5 ; D. 0,56.
p(A u B) = p(A) + p(B)- p(A n B) =0,2 +0,3 -0,2x0,3 = 0,44.
106. Du robinet ouvert d'un lavabo coule 127,5 L d'eau en 12 min 30 s. Quelle est la quantité d'eau qui s'est écoulée en 30 s ?
A. 12 L ; B. 6,8 L ;
C. 5,1 L vrai ; D. 3 kg.
12 min = 24 x30 s ; 12 min 30 s = 13 fois 30 s ; 127,5 / 25 =5,1 L.
107.
La lumière parcourt 300 000 km / s. Il y a environ 525 000 minutes dans
une année. La lumière met à peu près 4 ans et 3 mois pour aller de
proxima du Centaure à la terre. La distance entre cette étoile et la
terre est de :
A. 4,01625 1013 km vrai ; B. 4,2516 1031 km ; C. 4,1625 1013 km ; D. 4,25 1031 km.
4 ans et 3 mois = 4,25 ans ; 525 000 x 60 x 4, 25 x 300 000 = 4,01625 1013 km.
108. Un
téléviseur a une puissance de 90 W en marche et 10 W en veille. Sa
consommation s'exprime en kWh. Le téléviseur reste allumé 4 h par jour
et reste en veille le reste du temps. Combien consomme t-il par an (
365 jours).
A. 1500 ; B. 131,4 ; C. 682,56 ; D. 204,4 .Vrai
Consommation journalière : 90 x 4 +10 x 20 =360 +200 =560 Wh = 0,56 kWh.
Soit par an : 365 x 0,56 =204,4 kWh.
109. On mesure le débit d'un torrent au coeur d'une forêt. Le débit est constant, 3 m3 /s. Combien de litres d'eau coule en une journée ?
A. 259 200 000 vrai.; B.235 600 325 ; C. 350 000 ; D. 535 600.
3 000 x 3600 x 24 =2,592 108litres.
|
. .
|
110.
Un carreleur doit poser le carrelage dans une pièce rectangulaire
mesurant 6,48 m de large sur 13,5 m de long. Il souhaite poser des
carreaux les plus grands possibles et ne faire aucune découpe. Le
paquet de 20 carreaux carrés de cette taille coûte 65 €. Combien va
coûter le carrelage pour cette pièce ?
A. 800 ; B. 675. C. 581. D. 975. Vrai.
Plus grand diviseur commun à 648 et 1350 :
648 = 23 x 34. 1350 = 2 x 33 x 52. PGCD(648 ; 1350) = 2 x33 =54 cm.
Aire de la pièce : 648 x1350 =8,748 105 cm2.
Aire d'un carreau : 54 x54 =2916 cm2.
Nombre de carreaux : 300 soit 15 paquets ; 15 x 65 =975 €.
111.
ABCD est un trapèze rectangle en A et B tel que AB = 9, AD =3 et BC =
6. Soit H le projeté orthogonal de D sur la droite (BC). La largeur DC
est égale à :
A. 3 fois racine carré (10). Vrai.
B. 2 fois racine carré (10).
C. 9,82.
D. 12,15.
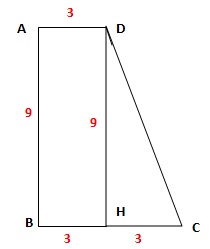
DC2 = 92 +32 =90 = 32 x10 ; DC = 3 fois racine carrée (10).
112. Quelle est l'image de 1-5½ par la fonction f(x) = -4 x2 -8*5½ ?
A.3*5½ ; B. 24 ; C. -2*5½. D. -24. Vrai.
-4(1-5½)2 -8*5½ =-4(1+5-2*5½)-8*5½ = -24.
113. Le point A(-3 ; 2) appartient-il à ?
A. Y =(x+9) / 3 Vrai
; B. y=-3x+1 ; C.Y=-3. ; D. y =1,5x+2.
(x+9) / 3 =(-3+9) / 3 = 2.
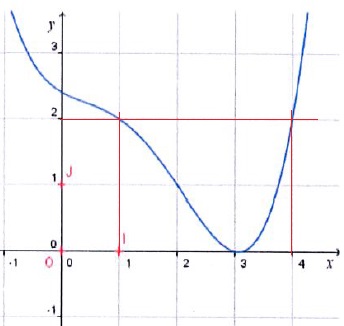
114. La fonction f est représentée par la courbe suivante. Les antécédents de 2 par cette fonction sont :
A. 0 et 2,5. B. 1. C. 1 et 4. Vrai.
D. 4.
115.
Dimension intérieures du four à micro-ondes H = 35 cm ; L = 40 cm et P
=30 cm. Un plat rectangulaire de dimensions 27 cm x 18 cm peut-il
rentrer dans le four ?
A. Oui, car le diamètre du cercle décrit par le plat est inférieur à la profondeur. Vrai.
B. Non, car le diamètre du cercle décrit par le plat est supérieur à la profondeur.
C. Je ne peux pas répondre car il manque des informations.
D. Non car la hauteur du plat ne permet pas à celui-ci de tourner.
116.
Un automobiliste effectue un aller-retour entre son travail et son
domicile, séparé de 60 km. A l'aller, il roule à 100 km / h et au
retour à 40 km / h. Sa vitesse moyenne sur le parcours est en km / h :
A. 57,14 Vrai ;
B. 60 km / h ;
C. 58,12 ; D. 62,5.
Aller : 60 / 100 = 0,6 heure ; retour : 60 / 40 =1,5 h ; total : 2,1 h.
Vitesse moyenne : 120 / 2,1 =57,14 km / h.
117. F est une fonction affine. On sait que f(2) = 5 et f(6) = -7. Quelle est son expression ?
A. f(x) = -3x+10.
B. f(x) = -2x+9.
C. f(x) = -3x+11. Vrai.
D. f(x) = -2x+10.
f(x) = ax +b ; 5 =2a+b ; -7 = 6a+b.
6a-2a =-7-5 ; 4a = -12 ; a = -3. Par suite b= 11.
118.
Une parisienne se promène à Paris.Elle souhaite connaître la distance
la séparant de la tour Eiffel dont elle connaît la hauteur ( 300 m).
Elle porte sa main à bout de bras. Avec la hauteur de ces 5 doigts ( 5
cm) elle arrive juste à caher la tour Eiffel. Son bras mesure 1 m de
long. A quelle distance est située la tour Eiffel ?
A. 600 m.
B. 6 km. Vrai.
C. 3 km.
D. 800 m.
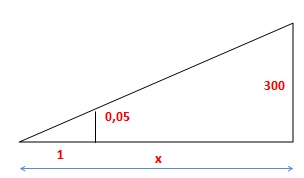
x = 300 / 0,05 = 6 000 m = 6 km
119. a décomposition en facteurs premiers de 27 000 000 est :
A. 26x33x56. Vrai.
B. 22x7x53.
C. 25x33x55.
D. 23x33x510.
33 x(2x5)6 .
120.
Dans un lycée, quel que soit le niveau, un élève peut être externe ou
demi-pensionnaire. l'arbre ci-dessous indique la répartition selon le
niveau et la qualité de l'élève ( E = externe ; DP=demi-pensionnaire).
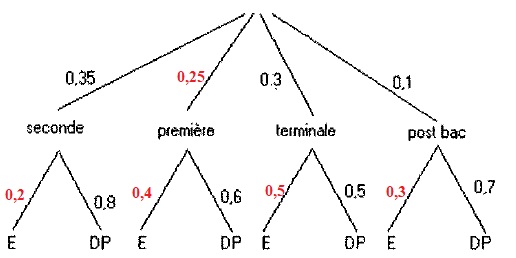
Les données manquantes sur chacune des branches sont respectivement :
A. 0,25 ; 0,2 ; 0,1 ; 0,8 ; 0,3 ; B. 0,25 ; 0,2 ; 0,4 ; 0,5 ; 0,3 ; vrai
C. je n'ai pas assez d'éléments pour compléter cet arbre.
D. 0,3 ; 0,2 ; 0,1 ; 0,5 ; 0,3.
|
|







