Mathématiques. Concours ingénieur territoriale 2009. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . .. .. ...... ... Problème I. Le plan est rapporté à un repère orthogonal d'origine O ; unité 3 cm sur chaque axe. On considère la courbe paramétrée C définie pour 0 < t < p/2 par : M(t) : x(t) = sin2(t)=(1-cos(2t)) / 2 ; y(t) = 4 sin(t) cos(t) = 2 sin (2t). 1. Calculer les coordonnées du point M(p/2-t) puis celle du milieu N(t) du segment [M(t)M(p/2-t)]. En déduire que C est symétrique par rapport à une droite D qu'on précisera. En déduire l'intervalle d'étude d'origine O. M(p/2-t)  : x=0,5(1-cos(p-2t)) =0,5(1+cos(2t)). y(t) = 2 sin (p-2t)=2 sin (2t). N(t) : abscisse : (1-cos(2t)) / 4 +(1+cos(2t)) / 4 =0,5. ordonnée : sin (2t) + sin (2t) = 2 sin (2t). La courbe est symétrique par rapport à la droite d'équation x = 0,5. On étudie la fonction sur 0 < t < p/4. 2. Calculer les dérivées des fonctions x et y. Préciser leur signe. x'(t) = sin(2t) > 0; y'(t) =4 cos(2t) > 0 si t appartient à 0 < t < p/4. x'(t) = sin(2t) > 0; y'(t) =4 cos(2t) < 0 si t appartient à p/4 < t < p/2. Former le tableau de variation de x(t) et de y(t). 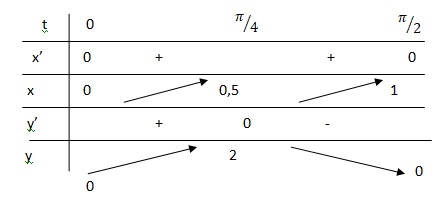3. Tracer la courbe C et préciser la tangente en chacun des points O, A = M(p/4) et B = M(p/2). 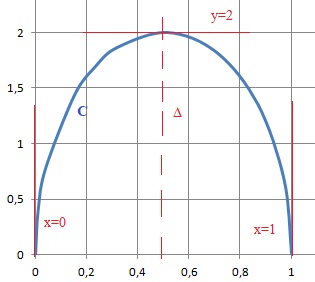4. On note (D) la partie du plan limitée par (C) et l'axe des abscisses. Calculer en cm2 l'aire S de (D). On utilise la formule de Green-Riemann : xdy =4  sin2(t) cos(2t) =2(1-cos(2t)) cos(2t) = 2[cos(2t)-cos2(2t)] = 2cos(2t) -(1+cos(4t) ). ydx = 2 sin2(2t) =1-cos(4t). xdy-ydx = 2cos(2t) -(1+cos(4t) )-1+cos(4t) =2cos(2t)-2. ½(xdy-ydx) = cos(2t)-1. Primitive de cos(2t)-1 : ½sin(2t) -t. Aire S = [½sin(2t) -t ]0p/2 =0 -p/2 -0= -1,57 unités d'aire ( courbe parcourue dans le sens anti-horaire). S = 1,57 unités d'aire ( courbe parcourue dans le sens horaire). Une unité d'aire = 9 cm2. 5. Déterminer l'équation de (C) sous la forme y = f(x). Exprimer sin(t) et cos(t) en fonction de x(t). sin(t) = x½ ; cos(t) = [1-sin2(t) ]½ = (1-x)½. y = 4 x½ (1-x)½= 4 [x(1-x)]½. ... .... Problème II. On considère les matrices suivantes à coefficients réels : 1. Calculer A2. En déduire qua A est inversible et calculer son inverse. Déterminant de A : 1-0-0+0*(-1)*1+0*(-1)*1-[1*0*0+1*0*0+1*(-1)*(-1)] = -1. Le dérminant n'est pas nul, la matrice est inversible. AxA = I ; A xA-1=I donc A=A-1. 2. Calculer les valeurs propres de A. 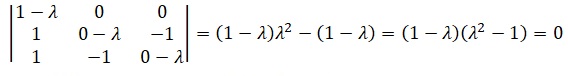l1 = -1 ; l2 = 1 ; l3 = 1. Déterminer une base et la dimension de chaque sous-espace propre de A. 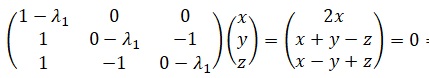2x = 0 ; x=0 ; x+y-z=0 soit y = z. Vecteur propre x1 (0 ; 1 ; 1). 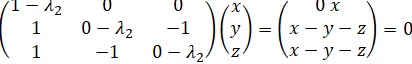0x = 0 ; x est quelconque  ; x-y-z=0. Par exemple : Vecteur propre x2 (2 ; 1 ; 1). De même pour l3. Vecteur propre x3 (0 ; 1 ; -1). 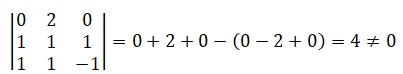Le déterminant n'est pas nul ; la famille (x1, x2, x3) est une base de R3. La matrice A est-elle diagonalisable ? Justifier. Les vecteurs propres x2 (2 ; 1 ; 1 ) et x3 (0 ; 1 ; -1) sont linéairement indépendants car non colinéaires. Ils constituent une base du sous espace propre E2. De même le vecteur propre x1 (0 ; 1 ; 1) constitue une base du sous espace propre E1. La dimension de chaque sous espace propre étant égale à l'ordre de multiplicité de la valeur propre correspondante, la matrice est diagonalisable. 3. Résoudre le système différentiel : dx/dt =x ; dy/dt = x-z ; dz/dt = x-y. x' -x = 0 ; x(t) = A et avec A une constante. y' -x+z = 0 ; z' -x+y = 0 ; y' +z'+y +z = 2x = 2Aet. On pose u = y +z ; u' +u = 2 A et ; u =y+z= B e-t + A et . On pose v = y -z ; v' -v = 0 ; v =y-z= C et . 2y = Be-t + (A+C) et  ; y(t) = ½Be-t +½(A+C)et. 2z = Be-t + (A-C) et  ; z(t) = ½Be-t +½(A-C)et. On vérifie : y' = -½Be-t +½(A+C)et ; x-z = Aet -½Be-t -½(A-C)et . z'= -½Be-t +½(A-C)et ; x-y = Aet -½Be-t -½(A+C)et. Déterminer la solution de ce système vérifiant x(0) = y(0) = 1 et z(0) = 0. x(0) =A = 1 ; y(0) =0,5 (1+B+C )= 1 ; B+C = 1.   z(0) = ½(B +1-C)=0 ; B-C = -1. B = 0 et C = 1. x(t) = et ; y(t) =et ; z(t) = 0. 4. On pose B = A+I. Calculer B2 en fonction de A et I; en déduire B2 en fonction de B. 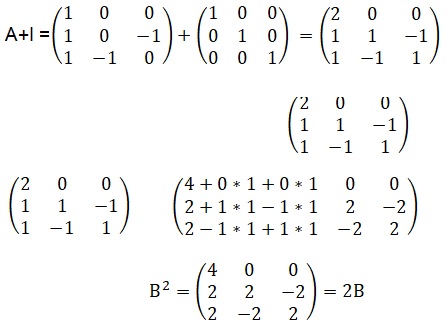Démontrer par récurrence que pour tout entier naturel n, n > 1 : Bn = 2n-1B. Initialisation : la propriété est vraie au rang 1. Hérédité : la propriété est supposée vraie au rang n :Bn = 2n-1B. Bn+1 = 2n-1B x B =2n-1x 2 x B =2nB.  La propriété est vraie au rang n+1. Conclusion : la propriété est vraie au rang 1 et héréditaire ; elle est vraie pour tout entier naturel n, n > 1

menu