La
foudre, prise de terre, pourquoi les paratonnerres sont-ils pointus ?
Concours interne ingénieur de
l'industrie et des mines 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
......
.....
|
A Le coup de foudre.
La
première phase d'un coup de foudre est la formation d'une pré-décharge
peu lumineuse appelée traceur qui progresse à travers l'air avec une
vitesse relativement faible. Elle prend naissance d'une part au sol (
traceur ascendant) d'autre part dans le nuage ( traceur descendant). Si
les traceurs se rejoignent, il s'établit une liaison conductrice entre
le nuage et le sol, un courant de forte intensité va circuler dans
l'air. La figure suivante donne un relevé in-situ de l'intensité I(t)
en kA d'un coup de foudre.
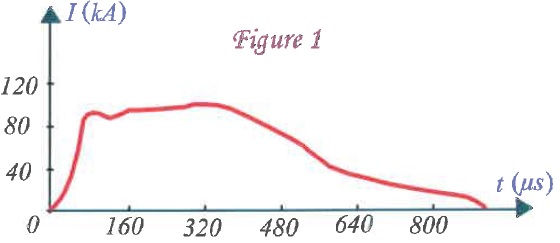
1. Evaluer la charge totale Q écoulée et l'intensité moyenne Im du courant de foudre.
Im ~70 kA sur une durée d'environ 500 µs.
Q = 70 103 x 500 10-6 ~ 35 C. ( aire sous la courbe).
2.
Estimer la différence de potentiel U entre le bas du nuage ( altitude 3
km) et le sol, sachant que le champ électrique vaut approximativement
27 kV m-1.
U = 27 103 x 3 103 =81 106 V ~100 MV.
3.
Si on admet que l'énergie dissipée lors de l'éclair est celle d'un
condensateur de charge Q sous la ddp U, quelle est la capacité de ce
condensateur ?
C = Q / U =35 / (81 106)=4,3 10-7 F.
4. Quels problèmes se posent pour récupérer cette énergie ?
Cette énergie est dispersée et aléatoire.
Trop d'énergie en trop peu de temps.
Il faudrait des millions de paratonnerres.
On ne sait pas stockée l'énergie électrique.
4. La foudre peut
engendrer des perturbations le long des circuits électriques. Expliquer
ce phénomène en s'appuyant sur les lois fondamentales de
l'électromagnétisme.
Lors
d'un coup de foudre, l'air est ionisé dans un canal conduisant du sol
au nuage orageux. On assimile l'éclair à un fil rectiligne infini,
d'axe Oz et de rayon a, parcouru par un courant I(t) uniformément
réparti dans une section droite et l'on se place dans
l'approximation des régimes quasi-stationnaires. Un point M au
voisinage de l'éclair sera repèré en représentation cylindrique, par
ces coordonnées ( r, q, z).
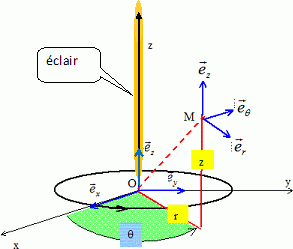
Des charges
négatives s'écoulent de l'atmosphère vers la terre : le sens de I(t)
est donc ascendant.
On s'intéresse à
l'expression du champ magnétique créé par l'éclair, toujours modélisé
par un fil infini de rayon a.
Expression du champ magnétique B(M) crée par
l'éclair.
Les vecteurs sont écrits en gras et en bleu.
L'axe
Oz est axe de symétrie du système ; une rotation autour de cet axe ne
modifie pas le champ : la variable q n'intervient donc pas
dans l'expression du champ.
Toute translation le long de l'axe Oz, ne modifie pas le champ : la variable z
n'intervient donc pas dans l'expression du champ.
Tout plan
contenant l'axe Oz est plan d'antisymétrie : le champ appartient donc
au plan contenant l'axe Oz et le point M d'où : Bq( r, z) =0.
Le champ est orthoradial : B(M) = B( r, t) eq.
On
considère un ensemble de fils parcourus par des courants, la
circulation C du champ magnétique le long d'une courbe fermée (G) quelconque est : 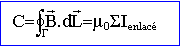
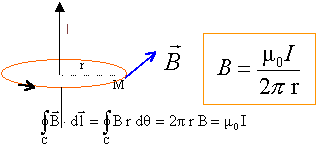
On calcule la circulation sur un
cercle : le champ est constant sur ce contour et reste tangent au
cercle.
Un coup de tonnere est une
décharge électrique caractérisée par des courants de fortes amplitudes
et de courtes durées.
On considère le circuit domestique d'alimentation d'une lampe. On
l'assimile, pour simplifier, à un cadre rectangulaire de surface S,
situé à la distance r de l'éclair. On modèlise l'éclair par un fil
rectiligne parcouru par un courant d'intensité I(t). Il produit un
champ magnétique d'expression B(r,t) = KI(t) / r.
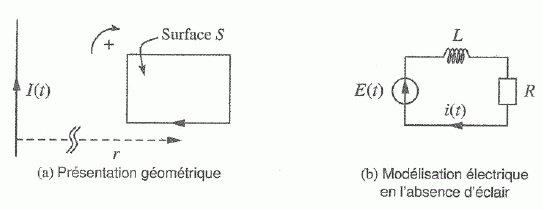 Le circuit électrique et
l'éclair sont coplanaires et suffisamment éloignés l'un de l'autre pour
que l'on puisse supposé homogène le champ magnétique au niveau du
circuit.
Le circuit électrique et
l'éclair sont coplanaires et suffisamment éloignés l'un de l'autre pour
que l'on puisse supposé homogène le champ magnétique au niveau du
circuit.
Ce circuit est le siège d'un phénomène d'induction.
Prise de terre.
Lorsque
le courant de foudre d'un impact direct sur un paratonnerre s'écoule
par la prise de terre, celle-ci doit présenter une faible résistance.
La limite est de 30 ohms. On considère la prise de terre constituée par
une demi-boule métallique pleine de rayon a, placée dans un sol de
résistivité r = 100 W m.
Un courant de foudre, d'intensité I, arrive via la tige paratonnerre
fixée au centre C de l'hémisphère. On traite le problème avec
l'électromagnétisme des régimes permanents.
1. Rappeler l'expression locale de la loi d'Ohm pour le sol.
2. Quelle est la forme des lignes de courant dans la terre ?
Ce sont des demi-droites pasant par le centre de la demi-boule métallique.
3. Donner le potentiel V(r) en fonction de r, I et r
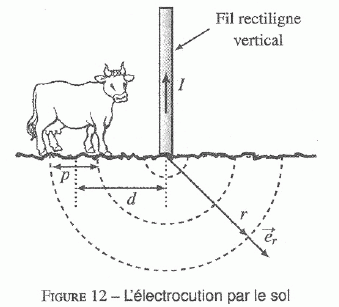
Modélisons
l'éclair traversant l'arbre par un fil rectiligne vertical semi-infini,
parcouru par un courant électrique ascendant d'intensité I = 15 kA.
Cette demi-droite prend fin au niveau du sol, où l'on suppose que la
densité volumique de courant est radiale, de la forme 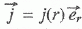 . l'étude est menée en régime stationnaire et l'on note g = 1 S m-1 la conductivité électrique du sol, inverse de sa résistivité . l'étude est menée en régime stationnaire et l'on note g = 1 S m-1 la conductivité électrique du sol, inverse de sa résistivité
Le courant traversant la demi- sphère de surface S = 2 pR2 est égal au courant I circulant dans l'éclair.
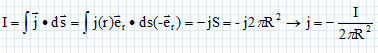
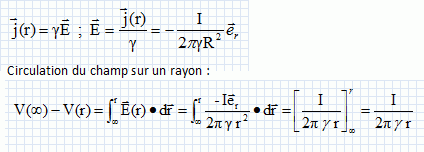
4. Quel est alors
le potentiel U de la demi-boule, le potentiel étant nul à
l'infini ? La résistance de terre R, étant définie par U = RI, calculer
le rayon a de l'hémisphère de telle manière que la valeur de la
résistance soit inférieur à 30 ohms.
La demi-sphère est équipotentielle : V =I / (2pg a).
U = V -Vinfini = V.
R = U / I = 1 / (2pg a). R < Rmax ; R < 30 ; a <1 / (2pg Rmax). a < 1 / (2 x3,14 x 0,01 x30) ; a < 0,53 m.
5. La tension de pas VP
est la différence de potentiel entre deux points de la surface du sol
distants de un mètre et situés sur une droite passant par le centre de
l'hémisphère. Calculer cette tension de pas à 100 m de la prise de
terre, pour un courant I = 50 kA.
V = I / (2pg r).
dV = -I dr / (2pg r2).
1 m << 100 m : |VP |~I Dr / (2pg d2) = 50 103 x 1 / (2 x3,14 x0,01 x 1002) ~ 80 V.
6. La résistance entre deux pieds d'une persone est R= 2,5 kW et que l'intensité de tétanisation est de 25 mA, quelle est la distance de sécurité au voisinage du paratonnerre ?
VP / R < 0,025.
I/ (2pg d2R) < 0,025 ; 50 103 / (2 x3,14 x0,01 x2500 d2) < 0,025 ;
318,5 / d2 < 0,025 ; d2 > 318,5 / 0,025 ; d2 > 12 739 ; d > 113 m.
Dr / (2pg d2) = 62,5 ; d2=1 / (2 x3,14 x0,01 x 62,5) =0,254 ; d = 0,50 m.
|
...
|
|
|
....
|
Pourquoi les paratonnerre sont-ils pointus ?
1. On considère un disque portant une densité surfacique de charge constante s et de rayon R. Quel est le potentiel électrostatique V(z) en un point P de l'axe Oz du disque ?
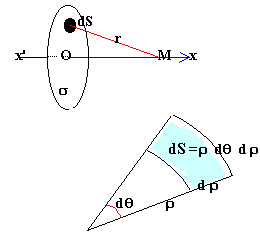
L'élément de surface dS du
disque porte la charge dq = s
dS et crée en M (OM=x) le potentiel
dV
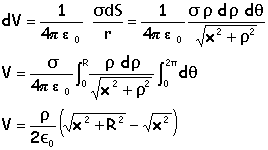
2. En déduire le champ électrostatique au point M
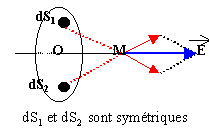 . .
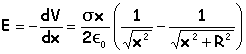
Le
champ résultant est dirigé vers le
disque si la charge est
négative.
3. Par passage à la limite, donner le champ créé par un plan.
R tend vers plus l'infini ; le champ tend vers E = s / (2e0).
4. Théorème de Coulomb. On considère un point P très proche de la surface d'un conducteur de forme quelconque. On appelle s la densité de charge surfacique à l'aplomb de P. Exprimer le champ en P.
La surface du conducteur en équilibre est une surface équipotentielle.
Les lignes de champ sont orthogonales aux surfaces équipotentielles. Le
champ au voisinage du conducteur est orthogonal à sa surface.
Très près de la surface du conducteur en équilibre électrostatique, la surface peut être considérée comme plane et infinie.
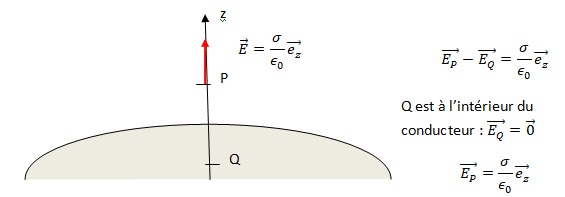
5 .Exprimer le
champ au voisinage d'un conducteur sphérique portant la charge totale
Q. En déduire le potentiel du conducteur sphérique.
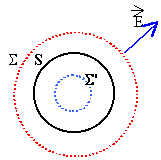 Par raison de symétrie, le champ est radial. Par raison de symétrie, le champ est radial.
champ électrique :(point
extérieur)
flux envoyé
à travers la sphère
S
de rayon r : définition du flux
: F=
4pr2E
th. de gauss :
charge
intérieure à S=
charge de S =4/3
pR3r.
F=
4/(3e0)
pR3r
E
=
R3r/(3e0r2) = Q / (4pe0r2).
Ce champ correspond à un potentiel V =Q / (4pe0r).
On relie une sphère métallique de rayon R1 par un conducteur de capacité négligeable à une autre sphère métallique de rayon R2 < R1. Elles prennent donc le même potentiel sans s'influencer mutuellement.

6. Que vaut le quotient des champs au voisinage de chaque sphère ? Expliquer pourquoi les paratonnerres sont pointus.
V1 =Q1 / (4pe0R1). V2 =Q2 / (4pe0R2).
Q1 = s1 * 4 pR12 ; Q2 = s2 * 4 pR22 ;
s1 * 4 pR12 / (4pe0R1) =s2 * 4 pR22 / (4pe0R2).
s2 =R1 / R2s1.
Le champ électrique est plus important au voisinage du conducteur de plus petit rayon.
Modèlisation d'une pointe :
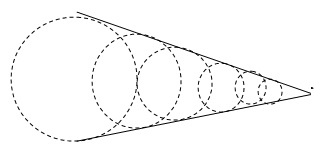
Les sphères modélisant la pointe sont au même potentiel et leur rayon
diminue. Plus on se rapproche de la pointe, plus le champ
électrostatique est grand.
|
|


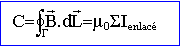



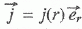
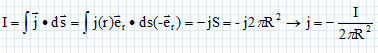
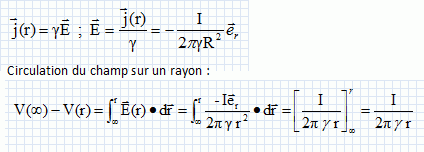

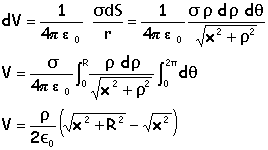

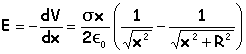

 Par raison de symétrie, le champ est radial.
Par raison de symétrie, le champ est radial.
