Une
petite glace.
Concours ITPE 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
......
.....
|
Réalisation
d'une glace.
On
mélange des fruits congelés avec du sucre et des blancs d'oeuf à
température ambiante. On cherche à déterminer la température finale du
mélange selon les proportions choisies.
Hypothèses
: les fruits sont assimilés à une masse m1 d'eau à la
température initiale T1 = -20°C.
Le mélange sucre + blancs d'oeufs est assimilé à une masse m2
d'eau pris à la température initiale T2 = 20°C.
On néglige la capacité thermique du récipient.
Capacité thermique de l'eau liquide : cl=4,18 kJ kg-1K-1
; de l'eau solide cs = 2,06 kJ kg-1 K-1.
Enthalpie massique de fusion de la glace DHfusion = 333 kJ
kg-1.
30.Le mélange se fait rapidement,
justifier que la variation d'enthalpie du mélange est nulle.
En
mélangeant rapidement fruits, sucre et blancs, les échanges avec le
milieu extérieur n'ont pas le temps de se réaliser.
31. On
note x = m2 / m1 et Tf la température
finale. Quelles sont les valeurs limites de Tf ?
Si m2 tend vers zéro, Tf = -20°C et si m1
tend vers zéro, Tf = 20°C.
32. On considère la
valeur particulière x' conduisant à un mélange de température finale
0°C complètement solide. Montrer que :
x' = cs(Tf-T1) / [cl(T2-Tf)+DHfusion]
Energie gagnée par les fruits : Q1 = m1cs(Tf-T1).
Energie cédée par le sucre et les blancs : Q2
= m2[cl(Tf-T2)-DHfusion].
Q1 +Q2
=0 ; m1cs(Tf-T1) = -m2[cl(Tf-T2)-DHfusion].
x' = cs(Tf-T1)
/ [cl(T2-Tf)+DHfusion].
33.
Déterminer la même expression x" correspondant à un mélange
complètement liquide.
Energie gagnée
par les fruits : Q1 = m1[cs(Tf-T1)+DHfusion].
Energie cédée par le sucre et les blancs : Q2
= m2cl(Tf-T2).
Q1 +Q2
=0 ; m1[cs(Tf-T1)+DHfusion] = -m2cl(Tf-T2).
x" = [cs(Tf-T1)+DHfusion] / [cl(T2-Tf)]
34. Tracer l'allure du graphe T(x)
et calculer x' et x".
x' = 2,06(Tf+20)
/ [4,18(20-Tf)+333] =(2,06 Tf +41,2) / (416,6-4,18 Tf).
416,6x'-4,18 Tf x' =2,06 Tf +41,2.
(2,06 +4,18 x')Tf =416,6x'-41,2 ;
Tf =(416,6x'-41,2) / (2,06 +4,18 x').
x" = [2,06(Tf+20)+333] / [4,18(20-Tf) ]=(2,06 Tf +374,2) / (41,2-4,18 Tf).
(41,2-4,18 Tf )x"=2,06 Tf +374,2 ; (2,06 +4,18 x")Tf
= -333 ; Tf = (-374,2 +83,6x) / (2,06 +4,18 x").
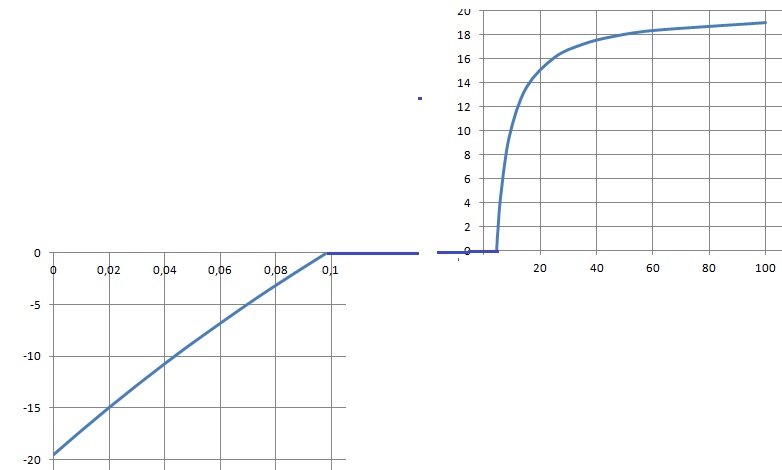
x' = 2,06(0+20) / [4,18(20-0)+333]=41,2 /416,6 ~0,1.
x" = [2,06(0+20)+333] / [4,18(20-0) ]=374,2 / 83,6=4,48.
35. Calculer Tf si m1
= 300 g et m2 = 80 g.
x =80 / 300 ~0,227.
0,1 < 0,227 < 4,48 ; le mélange est partiellement solide, sa
température est 0°C.
|
