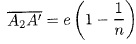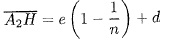Au palais des illusions. Concours ITPE 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. . . ...... ..... Avec une bougie. Deux bougies sont positionnées de part et d'autre d'une vitre. Le magicien allume la bougie devant la vitre : les spectateurs ont l'impression que les deux bougies sont allumées. On cherche à savoir comment placer la bougie derrière la vitre. d = 20 cm ; e = 1,0 cm épaisseur de la vitre ; n = 1,5 indice du verre. 23. Rappeler les lois de Descartes relatives à la réfraction et à la réflexion. 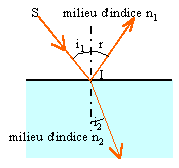Les trois rayons incident, réfléchi et réfracté sont dans le même plan ; l'angle d'incidence i1 est égal à l'angle de réflexion r. Les angles d'incidence i1 et réfracté i2 sont reliés par la relation : n1 sin i1 = n2 sin i2. 24. Reproduire le schéma ci-dessus et représenter le trajet des rayons lumineux issus de la flamme et ayant subi une réflexion sur la face avant de la vitre jusqu'à l'observateur. Où se trouve l'image de la bougie ? 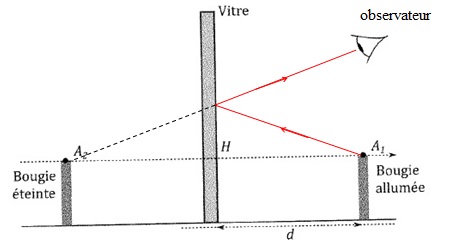L'image de la bougie est symétrique de la bougie allumée par rapport à la vitre. On s'intéresse au trajet des rayons lumineux issus de la bougie éteinte. 25. Construire le rayon transmis par la vitre. Quelle est sa direction ? 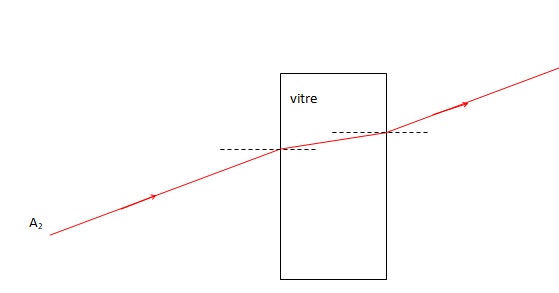Le rayon incident et le rayon transmis par la vitre sont parallèles. On note A2 le point source correspondant au haut de la bougie éteinte et A'  son image par transmission par la vitre. On se place dans les conditions de Gauss. 26. Rappeler les conditions de Gauss. Quelles en sont les conséquences pour les propriétés d'un système optique ? Les angles d'incidence des rayons par rapport à l'axe optique sont faibles. Le point d'incidence est proche de l'axe optique. Le système optique est approximativement stigmatique. 27. Montrer que la relation de conjugaison s'écrit :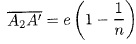 A2 objet, images A" puis A'. 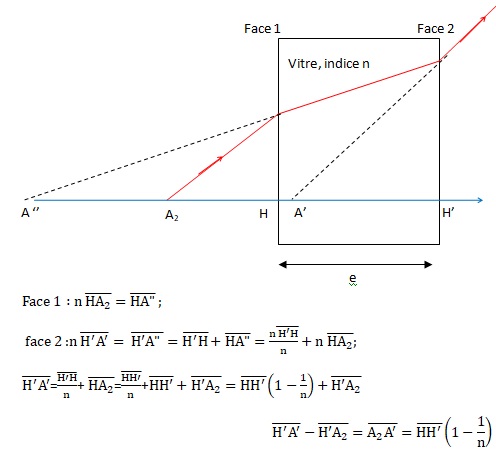28. En déduire que pour donner l'illusion au spectateur que la bougie éteinte est allumée, on doit avoir :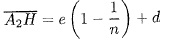 Le décalage entre l'image virtuelle et l'objet est e(1-1/n). Faire l'application numérique. La condition dépend-elle de la position du spectateur ? A2H ne dépend que de l'épaisseur de la vitre. A2H =1(1-1 /1,5 )+20 =20,3 cm. ... .... Avec un verre d'eau. Le magicien dispose d'un flotteur opaque, mince, de rayon R, au centre duquel est planté un clou perpendiculairement au plan du disque. La longueur du clou est h = 6 cm. Le disque est placé dans l'eau, le clou étant immergé. 29. A quel condition le clou est-il invisible pour un observateur placé dans l'air ? neau = 1,33. 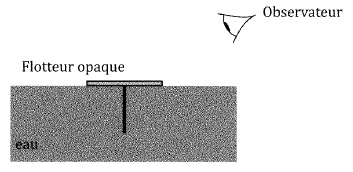A la limite de la visibilité, le rayon issu de la pointe du clou, après réfraction sur le dioptre eau/air, doit pénètrer dans l'oeil. 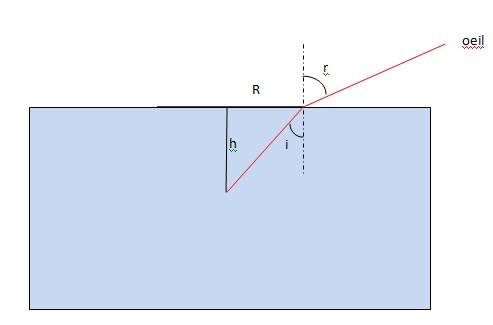Angle limite d'incidence pour que le rayon réfracté existe. sin ilim = 1/1,33 ~0,752 ; ilim ~49°. sin i = R /(R2+h2)½ ; La hauteur du clou étant fixée, ilim fixe une dimension maximale du rayon du disque opaque au delà de laquelle le clou reste invisible. Si cette condition est respectée, en plaçant l'oeil assez proche de la surface de l'eau on peut voir une partie du clou.   .

menu