Optique,
communication par fibre optique,
Concours ITPE 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicit�s adapt�es � vos centres
d’int�r�ts.
..
..
|
|
......
.....
|
Ph�nom�ne de r�flexion totale.
1. Que signifie le terme lumi�re monochromatique en optique ?
Une lumi�re monochromatique est caract�ris�e par une seule fr�quence.
On consid�re un rayon lumineux ( issu d'une lumi�re monochromatique)
arrivant sur � l'interface plane s�parant deux milieux d'indices
diff�rents, not�s n1 et n2 sous un angle d'incidence i.
2. Enoncer les lois de Descartes pour la r�flexion et la r�fraction.
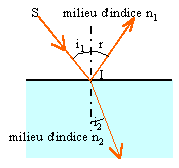
Les trois rayons incident, r�fl�chi et
r�fract� sont dans le m�me plan ;
l'angle d'incidence i1 est �gal �
l'angle de r�flexion r. Les angles d'incidence
i1 et r�fract� i2 sont
reli�s par la relation : n1 sin
i1 = n2 sin
i2.
3. Citer et d�crire une exp�rience montrant la d�pendance de l'indice de r�fraction du verre par rapport � la longueur d'onde.
Dispersion de la lumi�re par un prisme :
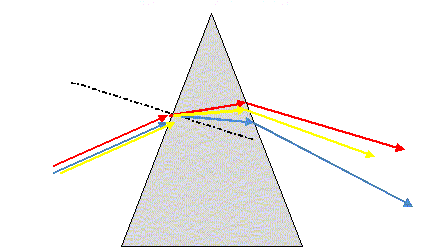
apr�s
avoir travers� le prisme de verre, les diff�rentes radiations color�es
constituant la lumi�re blanche sont d�vi�es diff�remment ; dans le
prisme les vitesses de propagation sont diff�rentes pour des radiations
de fr�quences diff�rentes.
4. On suppose dans cette partie que n1 > n2.
Montrer que si i > i0, aucun rayon r�fract� ne peut �merger et que le rayon incident est donc enti�rement r�fl�chi. Exprimer i0 en fonction de n1 et n2. On dit alors que le rayon incident subit une r�flexion totale.
n1 sin
i1 = n2 sin
i2 avec sin i2 < 1.
n1 sin
i0 = n2 ; sin
i0 = n2 / n1.
5. Dans le cas o� n1 = 1,500 et n2 = 1,470, donner la valeur num�rique de 90-i0.
1,47 / 1,5 = 0,980 ; i0 = 78,5 � ; 90-i0 ~ 11,5 �.
Fibre � saut d'indice.
Une fibre optique � saut d'indice est constitu�e d'un coeur cylindrique d'indice nc et d'une gaine cylindrique d'indice ng entourant le coeur avec ng < nc. Un rayon situ� dans le plan Oxy entre dans la fibre au point O avec un angle d'incidence q.
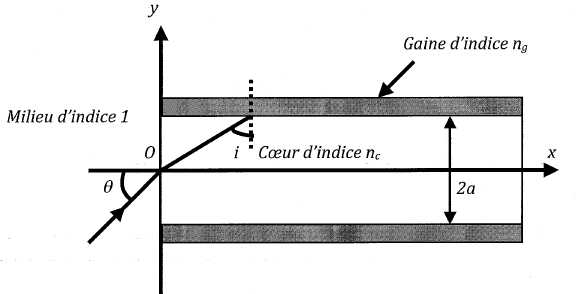
6. A quelle condition sur i, angle d'incidence � l'interface coeur-gaine, le rayon reste-t-il confin� � l'int�rieur du coeur ?
sin ilim = ng /
nc ; i doit �tre inf�rieur � ilim.
7. Montrer que la condition pr�c�dente induit une valeur limite qlim de q. En d�duire l'expression de l'ouverture num�rique ON = sin qlim.
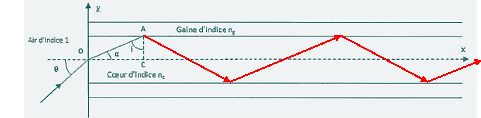
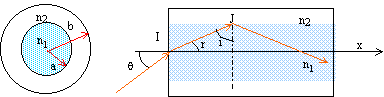
en I, dioptre air/coeur :
nair sin qi
= nc sin r ; sin qi
= nc sin r
(1).
en J, il y a r�flexion
totale : sin ilim = ng /
nc ; les angles i et r sont
compl�mentaires soit sin r = cos i.
(1) donne : cos i = sin q / nc ; sin q = nc cos i ; sin qlim = nc cos ilim ;
q doit donc �tre inf�rieur � qlim.
Un
raisonnement identique peut �tre fait pour tous les plans Oxy, quelle
que soit leur inclinaison par rapport au plan vertical. On dit qu'il
existe un c�ne d'acceptance associ� � la fibre permettant au rayon de
se propager par r�flexions totales dans la fibre.
sin ilim = ng /nc
; sin
qlim = nc cos ilim.
sin2
ilim =(ng
/nc)2
; cos2
ilim = sin2 q lim
/ n2c ; sin2
ilim +cos2
ilim =1.
1 = (ng
/nc)2
+ sin2 q lim
/ n2c ; n2c =n2g+sin2 q lim.
n2c -n2g=sin2 q lim
= ON2.
ON = (n2c -n2g)�.
ON = (1,52-1,472)�
=[(1,5+1,47)(1,5-1,47)]� =0,298.
|
...
|
|
|
....
|
8.
Exprimer la vitesse de propagation de la lumi�re dans la fibre en
fonction de la vitesse de la lumi�re dans le vide, not�e c, et de
l'indice du coeur nc.
v= c / nc.
On consid�re une fibre de longueur L. Le rayon entre dans la fibre avec un angle d'incidence q variable entre 0 et qlim.
9. Quel est le rayon qui traverse le plus rapidement la fibre ? Calculer la dur�e du parcurs Dtmin de ce rayon.
Le rayon correspondant � q = 0.
Dtmin = L / v = L nc / c.
10. Quel est le rayon qui met le plus de temps � traverser la fibre ? Calculer la dur�e du parcurs Dtmax de ce rayon.
Figure ci-dessus, expression de IJ
: ( on note h la projection de IJ sur l'axe de la
fibre).
cos r = h / IJ; or sin
qi
= nc sin r ; cos� r + sin� r = 1
;
h� / IJ� +( sin
qi
/ nc )� = 1 ; h / IJ = [1-( sin
qi
/ nc )�
]�.
Le rapport entre la longueur L de
la fibre et le trajet d suivi par la lumi�re est :
L/d =[1-( sin qi
/ nc )�
]�
d = L[1-( sin
qi
/ nc )�
]-� soit pour l'angle qlim : d = L[1-( sin
qlim
/ nc )�
]-� .
d =L[1-( n2c -n2g)
/ n2c )
]-� =L(n2g)
/ n2c ) -�=Lnc / ng.
Dtmax = d nc / c =Ln2c / (ng c).
11. En d�duire que l'intervalle de temps Dt entre le temps de parcours minimal et maximal s'�crit : Dt = nc(nc-ng)L / (ngc).
Dt=Ln2c / (ng c)- L nc / c = L nc[nc/ (ng c)-1/c]=L nc[nc/ (ng c)-ng / (ng c)]= nc(nc-ng)L / (ngc).
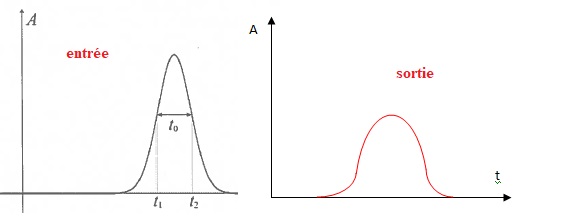
On injecte � l'entr�e de la fibre une impulsion lumineuse d'une dur�e caract�ristique t0 = t2-t1 form� par un faisceau de rayons ayant un angle d'incidence compris entre 0 et qlim. La figure ci-dessous repr�sente l'allure de l'amplitude du signal en fonction du temps.
12. Reproduire l'allure du signal lumineux � la sortie de la fibre. Quelle est la dur�e t'0 de cette impulsion de sortie ?
t'0=t0+Dt.
13.
Le codage binaire de l'information consiste � envoyer des impulsions
lumineuses p�riodiquement avec une fr�quence d'�mission f. On
suppose t0 n�gligeable devant Dt. Quelle relation existe-t-il entre la fr�quence maximale d'�mission fmax et la longueur L de la fibre ?
Il ne faut pas que deux signaux
cons�cutifs se superposent � la sortie
d'o� la fr�quence maxi :
fmax = 1 / t'0 ~1/ Dt = ngc/ [ nc(nc-ng)L ].
14. Pour L = 100 m, calculer fmax. Commenter.
Pour L = 100 m ; fr�quence maximale de r�p�tition fmax = 1,5 x 3 108 / (1,47 x0,03 x100)=1,02 108 Hz.
|
|
Optique de focalisation.
Il est n�cessaire pour optimiser l'intensit� lumineuse se propageant
dans la fibre d'adapter en entr�e une lentille convergente mince de
focale f '.
Le faisceau incident est suppos� parall�le � l'axe optique de diam�tre d = 1,0 mm, inf�rieur au diam�tre de la lentille.
15. On se place dans les conditions de Gauss. Pr�ciser en quoi consistent les conditions de Gauss.
L'objet
doit �tre de petites dimensions et plac� au voisinage de l'axe optique
principal du syst�me optique. On �limine ainsi les rayons lumineux trop
inclin�s sur l'axe optique. Les syst�mes optiques poss�dent en g�n�ral
un axe de sym�trie appel� axe optique.
16. Sur un sch�ma,
tracer le faisceau lumineux apr�s travers�e de la lentille. En d�duire
l'expression de l'angle d'ouverture du faisceau apr�s la lentille.
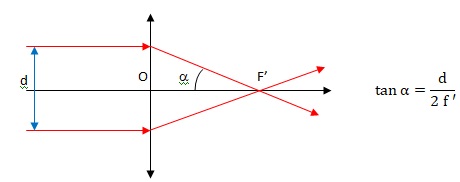
Les angles �tant petits, tan a ~ a ; 2 a ~ d / f '.
7.
Justifier que pour que l'int�gralit� du faisceau lumineux p�n�tre �
l'int�rieur de la fibre optique, on doit avoir : f ' > d / tan qlim.
a doit donc �tre inf�rieur � qlim.
18. Quel ph�nom�ne limite la focalisation ?
La diffraction.
|
|
|
