Fonctions.
Concours ITPE 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
...
|
|
......
.....
|
1. Etude d'une fonction.
Soit f la fonction définie sur R*+ par : f(t) = t-1-ln(t).
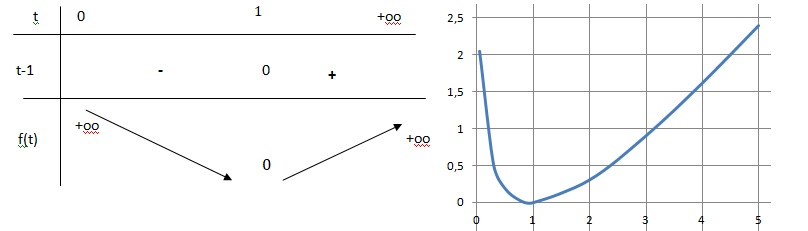
a. Calculer les limites de f en 0 et en +oo.
Quand t tend vers zéro, f(t) est équivalent à -ln(t) ;ln(t) tend vers moins l'infini et f(t) tend vers plus l'infini.
Quand t tend vers plus l'infini : f(t) = t(1-1 / t -ln(t) / t).
Par croissance comparée ln(t) / t tend vers zéro ; 1 /t tend vers zéro ; f(t) tend vers + oo.
b. Dresser le tableau de variation de f.
f '(t) = 1-1 / t = (t-1) / t.
2. Calcul d'intégrale.
a. Soit x un réel de ]0 ; 1[. Justifier l'existence de l'intégrale I = 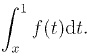
f(t) est continue sur cet intervalle, donc f admet des primitives sur ]0 ; 1[.
Primitive de f(t) : F(t) =t2 / 2-t-[t ln(t) -t] =t2 / 2-t ln(t).
F(0+) = 0 ; F(1) = 0,5, valeurs finies, donc l'intégrale existe.
b.
Expliciter cette intégrale. Déterminer sa limite en 0+.
Primitive de f(t) : F(t) =t2 / 2-t-[t ln(t) -t] =t2 / 2-t ln(t).
F(1)-F(x) =0,5 -(x2 / 2-x ln(x))=0,5 -0,5x2+xln(x).
Quand x tend vers 0+ : x2 tend vers zéro ; x ln(x) tend vers zéro et F(1)-F(x) tend vers 0,5.
3. Calcul et encadrement d'une somme.
Soit n un entier naturel non nul.
a. Démontrer que :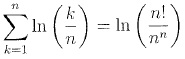
ln(1/n) + ln(2/n) +...ln(k /n) = ln(1)+ln(1/n) + ln(2) +ln(1/n) +...ln(k)+ln(1/n) = n ln(1/ n)+ln(1 x2x...x n)= ln(1/nn)+ln(n!) = ln(n! / nn).
b. En déduire l'égalité suivante :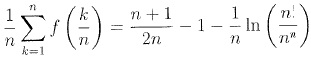
f(1/n) =1/n-1 -ln(1/n) ; f(2/n) =2/n-1 -ln(2/n) ; f(n/n)=f(1) =0 ;
f(1/n) + f(2/n) +....f(n/n) =1/n(1 +2 +...+n) -n -[ln(1/n)+ln(2/n)+...ln(n/n)].
=(1+n) / 2 -n- ln(n! / nn).
Puis diviser chaque terme par n.
c. Soit k un entier tel que 2 < k < n.
En utilisant la monotonie de f sur ]0 ; 1[ démontrer que quelque soit t appartenant à ([k-1) /n ; k /n], f (k/n) < f(t).
f(t) est strictement décroissante sur cet intervalle.
k / n est la borne supérieure de l'intervalle : t < k/ n ; f(k / n) < f(t).
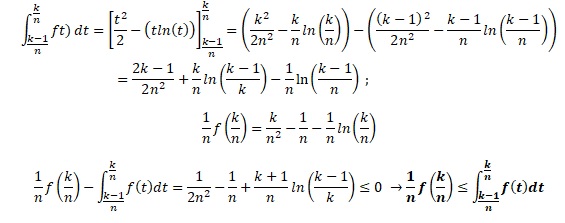
d. Déduire du résultat précédent l'inégalité suivante :
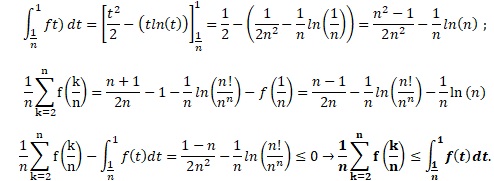
e. Etablir la relation suivante :
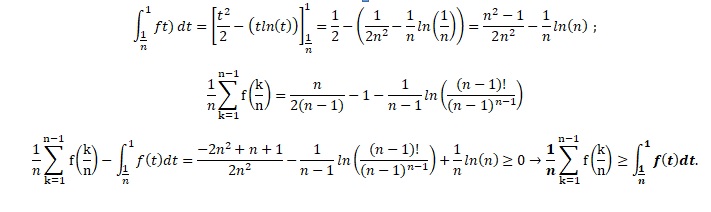
Par suite : 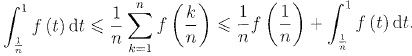
4. Conclusion :
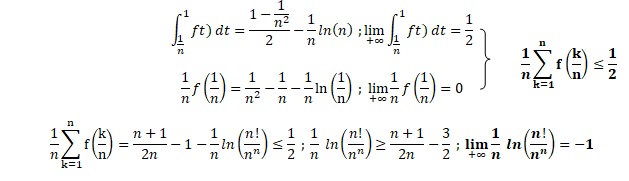
|